ppt《最短路径问题》_第1页
ppt《最短路径问题》_第2页
ppt《最短路径问题》_第3页
ppt《最短路径问题》_第4页
ppt《最短路径问题》_第5页
已阅读5页，还剩10页未读， 继续免费阅读

下载本文档

版权说明：本文档由用户提供并上传，收益归属内容提供方，若内容存在侵权，请进行举报或认领

文档简介

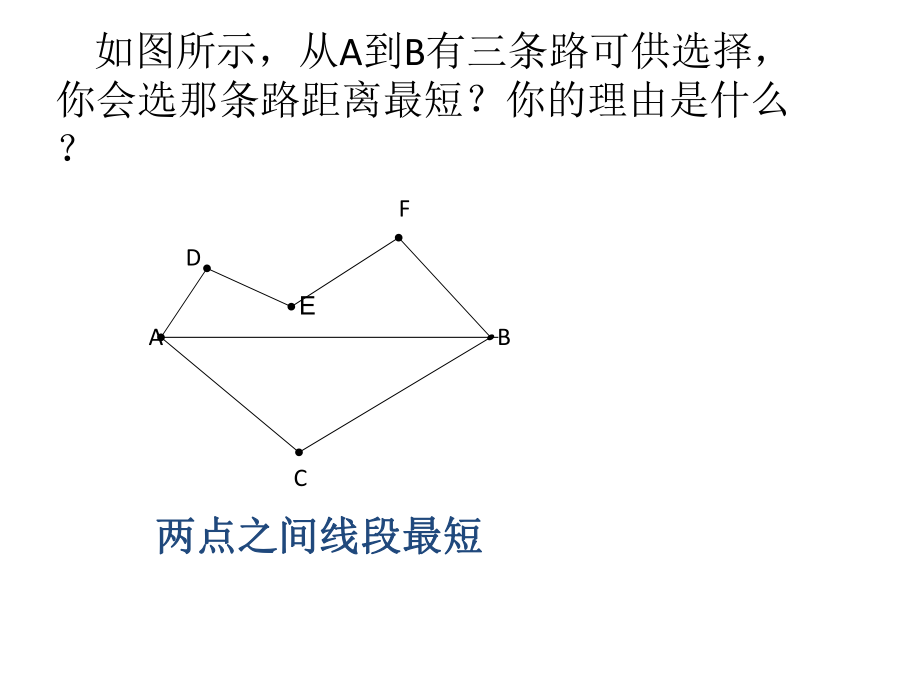
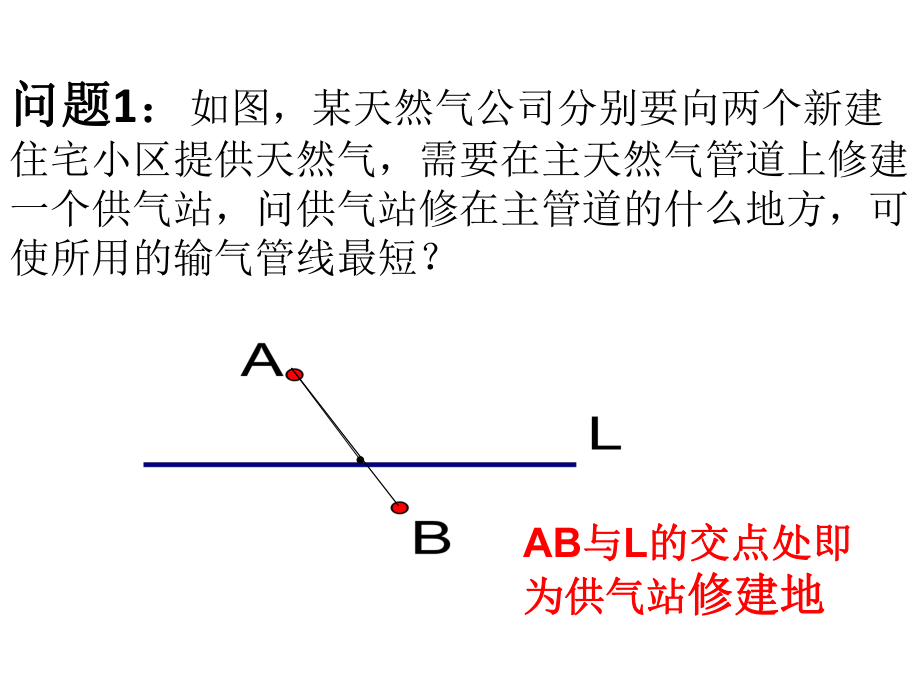
1、13.4课题学习最短路径问题讲师：李江源1.情境引入 前面我们研究过一些关于“两点的所有连线中，线段最短”“连接直线外一点与直线上各点的所有线段中，垂线段最短”等的问题，我们称它们为最短路径问题。如图所示，从A到B有三条路可供选择，你会选那条路距离最短？你的理由是什么？ F D E A B C 两点之间线段最短两点之间线段最短问题问题1：如图，某天然气公司分别要向两个新建住宅小区提供天然气，需要在主天然气管道上修建一个供气站，问供气站修在主管道的什么地方，可使所用的输气管线最短？AB与与L的交点处即的交点处即为供气站为供气站修建地修建地 如图1牧马人从A地出发，到一条笔直的河边L饮水，然后到B

2、地。牧马人到河边的什么地方饮水，可使所走的路径最短？L AB 如果将河L抽象成一条直线，把牧马人饮水的地方看成C点，这样C就为直线L上的一个动点，那么上面的问题就可以转化为：当点C在L的什么位置时，AC与BC的和最小。思考思考。如果我们把点B作关于L的对称点B，同时对直线L上的任一点C，都保持CB与CB的长度相等，就可以把问题转化为异侧的问题。你能利用轴对称的相关知识，找到符合条件的点B吗？ 追问：如何将点B移到L的另一侧B处，满足直线L上的任意一点C，都保持BC与BC的长度相等？问题： 你能用所学知识证明AC+BC最短吗？ B A C L B 证明：如图,在直线L上任取一点C（与点C不重合）

3、，连接A C,B C,CB. 由轴对称的性质知 BC= BC BC= CB.所以AC+BC=AC+ BC=A B A C+BC= A C+ BC又因为在三角形A BC中A B A C+BC,所以 AC+BC A C+BC即 AC+BC最短。 B A C C L B 练习巩固练习巩固： 如图，一个旅游船从大桥AB的P处前往山脚下的Q处接游客，然后将游客送往河岸BC上，再返回P处，请画出旅游船的最短路径基本思路基本思路 由于两点之间线段最短，所以可以先连接PQ，线段PQ为旅游船最短路径中的必经路线，将河岸抽象为一条直线BC，这样问题就转化为“点P,Q都在BC的同侧如何在BC上找一点S使得PS+QS最短”。练习练习1、 如图，直线L是一条河，P、Q是两个村庄，欲在L上的某处修建一个水泵站，向P、Q两地供水，现有四种铺设方案，图中实线表示铺设的管道，则所需管道最短的是（ ）思考：思考：已知如图，点A和两条直线m和n，你能在直线m、n上分别找一点P、Q，使得AP+PQ+AQ的值最小吗？小结：小结： 我们利用做对称点（轴对称变换）

人人文库> 全部分类> 教育资料 > 课件下载

温馨提示

  • 1. 本站所有资源如无特殊说明，都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
  • 2. 本站的文档不包含任何第三方提供的附件图纸等，如果需要附件，请联系上传者。文件的所有权益归上传用户所有。
  • 3. 本站RAR压缩包中若带图纸，网页内容里面会有图纸预览，若没有图纸预览就没有图纸。
  • 4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
  • 5. 人人文库网仅提供信息存储空间，仅对用户上传内容的表现方式做保护处理，对用户上传分享的文档内容本身不做任何修改或编辑，并不能对任何下载内容负责。
  • 6. 下载文件中如有侵权或不适当内容，请与我们联系，我们立即纠正。
  • 7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。

最新文档

评论

0/150

提交评论