华南师范大学电磁学第一章静电学的基本规律(高斯定理)

1、1 四、高斯定理及其应用四、高斯定理及其应用 1.电场线（电力线）电场线（电力线） 2.电通量电通量 3.静电场的高斯定理静电场的高斯定理 4. 高斯定理在解场方面的应用高斯定理在解场方面的应用 附录附录1：静电应用（图片）：静电应用（图片） 附录附录2：静电场高斯定理的证明：静电场高斯定理的证明 附录附录3：如何理解均匀带电球面内场强为：如何理解均匀带电球面内场强为0？2定性定性:定量定量:疏密疏密垂直面积垂直面积 规定条数规定条数 （1）规定）规定 方向：方向：电场线电场线上每一点的切线方向表示该上每一点的切线方向表示该点的电场强度方向点的电场强度方向； 大小：大小：E1. 电场线（电力线

2、）电场线（电力线）用一族空间曲线形象描述场强分布用一族空间曲线形象描述场强分布电场线电场线(electric field line)过去称为过去称为电力线电力线P3SEddSEdd式中的式中的d称为通过该面积元的电通量称为通过该面积元的电通量定量规定：定量规定： 通过垂直于通过垂直于 的单位面积的电场线条数等的单位面积的电场线条数等于该区域的电场强度值，即，于该区域的电场强度值，即，EEdS 43)电场线有头有尾，不会形成闭合曲线电场线有头有尾，不会形成闭合曲线.（2）电场线的性质）电场线的性质1)电场线起始于正电荷电场线起始于正电荷(或无穷远处或无穷远处)，终止于，终止于负电荷负电荷(或无穷

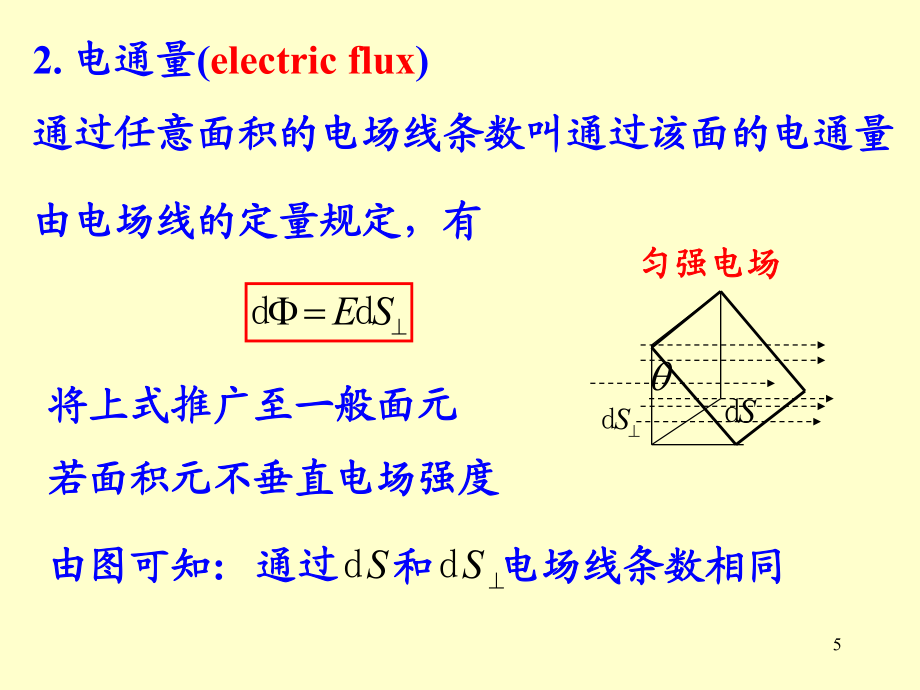
3、远处或无穷远处) ，不会在没有电荷处中，不会在没有电荷处中断断.2)两条电场线不会相交，也不会相切两条电场线不会相交，也不会相切.这些性质是由静电场的基本性质和场的单这些性质是由静电场的基本性质和场的单值性、有限大小性决定的值性、有限大小性决定的.并且可用并且可用静电场静电场的基本性质方程的基本性质方程加以证明加以证明.5SdSd将上式推广至一般面元将上式推广至一般面元若面积元不垂直电场强度若面积元不垂直电场强度由图可知由图可知: 通过通过SSdd和和电场线条数相同电场线条数相同匀强电场匀强电场SEdd由电场线的定量规定，有由电场线的定量规定，有2. 电通量电通量(electric flux)

4、 通过任意面积的电场线条数叫通过该面的电通量通过任意面积的电场线条数叫通过该面的电通量6sd由图可知由图可知: 通过通过SSdd和和电场线条数相同电场线条数相同SEddEnSSdd cosSEdSdSd匀强电场匀强电场令令SEdd电通量的基本定义式电通量的基本定义式是面元是面元dS的法线方向与该处的法线方向与该处的电场强度方向之间的夹角的电场强度方向之间的夹角7SSSEddSEdd通过任意面积元的电通量通过任意面积元的电通量通过任意曲面的电通量：通过任意曲面的电通量：S把曲面分成许多个面积元把曲面分成许多个面积元每一面元处视为匀强电场每一面元处视为匀强电场SdE8物理上有实际意义的是求物理上有

5、实际意义的是求通过闭合面的电通量通过闭合面的电通量讨论讨论SEdd1) )有正有正 有负有负若取若取如如实蓝箭头实蓝箭头所所示的法线方向，则示的法线方向，则 若取如若取如虚红箭头虚红箭头所所示的法线方向，则示的法线方向，则SSdE正负取决于正负取决于面元的法线面元的法线方向的方向的选取选取SEd 0SEd 0对于非闭合面，面元的正方向可以任取，对于非闭合面，面元的正方向可以任取，9规定：规定：面元方向面元方向SESdSdsEd0sEd几何含义：通过闭合曲面的电场线的几何含义：通过闭合曲面的电场线的净净条数条数10 3. 静电场的高斯定理静电场的高斯定理(Gauss theorem) (1) 表

6、述表述 在静电场内在静电场内 任一闭合面的电通量任一闭合面的电通量等于这闭合面所包围的电量的代数和除以等于这闭合面所包围的电量的代数和除以 0 SsdE0(内）SiiSqSE内内d（严格证明见附录（严格证明见附录2）qi11(2) 高斯定理关系式的导出高斯定理关系式的导出思路思路：1）以点电荷场为例）以点电荷场为例 取包围点电荷的高斯面取包围点电荷的高斯面 取不包围点电荷的高斯面取不包围点电荷的高斯面 2）推广到一般）推广到一般推导：推导：1）场源电荷是电量为）场源电荷是电量为Q的点电荷的点电荷 高斯面高斯面包围包围该点电荷该点电荷12高斯面如图高斯面如图QS通过该高斯面的电通量？通过该高斯面

7、的电通量？根据电场线的连续性根据电场线的连续性等于以点电荷为球心的等于以点电荷为球心的任意半径的球面的电通量任意半径的球面的电通量r计算通过计算通过球面球面的电的电通量通量SdSEeddSEdE通过高斯球面任一面元通过高斯球面任一面元的电通量是的电通量是Sd13SSSESEdd24 rE 22044rrQ0Q等于高斯面内电量代数和除以等于高斯面内电量代数和除以 02) )场源电荷仍是点电荷场源电荷仍是点电荷 但高斯面但高斯面不不包围电荷包围电荷QS 因电场线连续，故电通量为零因电场线连续，故电通量为零 等于高斯面内电量代数和除以等于高斯面内电量代数和除以 03) )推广推广:利利用叠加原用叠加

8、原理理0(内）SiiSqSEd通过高斯球面的电通量通过高斯球面的电通量SSE d14讨论讨论3) )高斯定理是静电场的基本性质方程之一，高斯定理是静电场的基本性质方程之一，它它表明静电场是表明静电场是有源场有源场，它要求电场线在无，它要求电场线在无电荷处不能中断电荷处不能中断. 1) ) 中中, , 是面元是面元 所在处的场强所在处的场强. .SSEdESd只有只有闭合面内闭合面内的的电荷电荷对对电通量电通量 有贡献有贡献.2) ) 并非只是由并非只是由闭合面内的电荷产生，而是闭合面内的电荷产生，而是由空间由空间所有电荷共同产生的，但是闭合面内所有电荷共同产生的，但是闭合面内、外的电荷对电通量

9、、外的电荷对电通量 的贡献不同的贡献不同.SSEdESSEd4) )对于运动电荷产生的电场及迅变电磁场，对于运动电荷产生的电场及迅变电磁场，库仑定律不再成立，但高斯定理仍然成立库仑定律不再成立，但高斯定理仍然成立. .15 常见的电量分布的常见的电量分布的很好的很好的对称性：对称性： 球对称球对称 柱对称柱对称 面对称面对称均均匀匀带带电电的的球体球体球面球面(点电荷点电荷)无限长的无限长的柱体柱体柱面柱面带电线带电线无限大的无限大的平板平板平面平面4. 高斯定理在高斯定理在求解场强求解场强方面的应用方面的应用利用高斯定理求解利用高斯定理求解E较为方便较为方便对电量的分布具有对电量的分布具有很

10、好的很好的对称性情况下对称性情况下16举例目的：举例目的：1) )清晰清晰用高斯定理解题的用高斯定理解题的步骤步骤2) )通过解题通过解题明确明确用高斯定理解题的用高斯定理解题的条件条件3) )简单的解作为基本结论简单的解作为基本结论记住记住 并且能并且能熟练使用熟练使用 理论理论是建立在是建立在理想模型理想模型之上的之上的注意注意电量分布没有电量分布没有很好的很好的对称性时，虽然对称性时，虽然不能用高斯定理求场强，但高斯定理仍然成立！不能用高斯定理求场强，但高斯定理仍然成立！17例例1 求电量为求电量为q 半径为半径为R 的的均匀带电均匀带电球面球面的的 电场强度分布电场强度分布 q第第1步

11、：步：根据电荷分布的对称根据电荷分布的对称性，选取合适的经过场点的高性，选取合适的经过场点的高斯面斯面(闭合面闭合面)解解:取取过场点过场点P的以球心的以球心O 为球心的球面为球心的球面ESSEdSSEdSSE d24 rERoPrSSd第第2步：步：从高斯定理表达式的左方入手从高斯定理表达式的左方入手 计算通过高斯面的电通量计算通过高斯面的电通量18第第4步：步：根据高斯定理列方程、解方程根据高斯定理列方程、解方程0)(24内SiiqrEEqrii402 第第3步：步：求高斯面内电量代数和求高斯面内电量代数和24 rESESdQrSRoP0iiqRr19第第5步：得解步：得解rER均匀带电球

12、面电场分布均匀带电球面电场分布0204Rq0思考：思考：0ERr1）球面）球面内内场强为场强为零零 到球面到球面外突变外突变 ，物物理上合理吗？理上合理吗？2）若选过场点）若选过场点P的的任意闭合曲面，高任意闭合曲面，高斯定理是否成立？斯定理是否成立？能否求出场强的分能否求出场强的分布？布？3）能否这样证明能否这样证明球面内的场强：球面内的场强：“因为球面内没因为球面内没有电荷，所以场有电荷，所以场强为零强为零”，对吗？，对吗？20例例2 求电量为求电量为q 半径为半径为R 的的均匀带电均匀带电球体球体的的 电场强度分布电场强度分布 q第第1步：步：根据电荷分布的对称根据电荷分布的对称性，选取

13、合适的经过场点的高性，选取合适的经过场点的高斯面斯面(闭合面闭合面)解解:取取过场点过场点P的以球心的以球心O 为球心的球面为球心的球面ESSEdSSEdSSE d24 rERoPrSSd第第2步：步：从高斯定理表达式的左方入手从高斯定理表达式的左方入手 计算通过高斯面的电通量计算通过高斯面的电通量21第第4步：步：根据高斯定理列方程、解方程根据高斯定理列方程、解方程0)(24内SiiqrEEqrii402 第第3步：步：求高斯面内电量代数和求高斯面内电量代数和24 rESESdQrSRoPqRrqRrii33iiqqRr22第第5步：得解步：得解rER均匀带电球体电场分布均匀带电球体电场分布

14、0204Rq0rrRqERr03034204rqERr23例例3 均匀带电的无限长的直线均匀带电的无限长的直线线密度线密度对称性的分析对称性的分析rPEd取合适的高斯面取合适的高斯面lr计算电通量计算电通量SsEd两底面侧面sEsEddrlE 2sdEsd利用高斯定理解出利用高斯定理解出E02lrlErE0224例例4 求面电荷密度为求面电荷密度为的的均匀带电无限大平均匀带电无限大平面的场强分布面的场强分布. 解：解：由对称性分析易知空间的由对称性分析易知空间的场强必垂直于带电平面场强必垂直于带电平面, 而且而且与带电平面距离相等的点场强与带电平面距离相等的点场强大小相同大小相同.由于圆筒的侧

15、面上各点的由于圆筒的侧面上各点的 与侧面平行，故与侧面平行，故EESESSdESdESdE22底两底面侧面又又内SiSq001据高斯定理可得：据高斯定理可得：02SES 02E 选一个过场点选一个过场点P、轴线与带电平、轴线与带电平面垂直的的圆筒形高斯面，两底面面垂直的的圆筒形高斯面，两底面到带电平面距离相等，到带电平面距离相等，如图所示如图所示. .S底底poSEE25求电场强度求电场强度E分布的三种方法分布的三种方法1.1.利用点电荷场强公式和场强叠加原理利用点电荷场强公式和场强叠加原理2.2.利用已知场强公式和场强叠加原理利用已知场强公式和场强叠加原理3.3.利用高斯定理（电荷分布具有很

16、好的利用高斯定理（电荷分布具有很好的对称性）对称性）第一章结束第一章结束26附录附录1 1： 静电应用静电应用(图片图片) 海底探雷海底探雷27 静电喷漆静电喷漆 静电除尘静电除尘28 带电木梳吸水带电木梳吸水29附录附录2 2：高斯定理的立体角法证明高斯定理的立体角法证明1. .介绍立体角的定义介绍立体角的定义2. .证明证明30r1) )平面角平面角 由一点发出的两条射线之间的夹角由一点发出的两条射线之间的夹角 记做记做 d cos0rlrlddd单位：弧度单位：弧度1. .立体角的概念立体角的概念l dd设射线长为设射线长为r ，线段元线段元dl对某点所张的平面角：对某点所张的平面角：0

17、l ddl0是以是以r为半径的圆弧为半径的圆弧 是线段元是线段元dl与与dl0之间的夹角之间的夹角312) )立体角立体角 面元面元dS 对某点所张的角叫做立体角对某点所张的角叫做立体角 即锥体的即锥体的“顶角顶角”单位：球面度单位：球面度rdSd0Sdcos220rSrSddd对比平面角有对比平面角有定义式定义式:dS0是以是以r为半径的圆锥对应的球面元为半径的圆锥对应的球面元 是面元是面元dS与球面元与球面元dS0间的夹角间的夹角32弧度弧度闭合曲面对面内一点所张的立体角闭合曲面对面内一点所张的立体角球面度球面度420SSrSddld闭合平面曲线对曲线内一点所张的平面角闭合平面曲线对曲线内

18、一点所张的平面角coslrld00lrld233库仑定律库仑定律 + 叠加原理叠加原理思路：思路：先证明点电荷的场先证明点电荷的场 然后推广至一般电荷分布的场然后推广至一般电荷分布的场1) 源电荷是点电荷源电荷是点电荷在该场中取一包围点电荷的闭合面在该场中取一包围点电荷的闭合面(如图示如图示)2.高斯定理的证明高斯定理的证明 qSddE在闭合面在闭合面S上任取面元上任取面元Sd该面元对点电荷所张的该面元对点电荷所张的立体角立体角d点电荷在面元处的场强为点电荷在面元处的场强为ES34SrrqSEddd420d04qddSSqSE040)(内SiiSqSEd204cosrsqdSqd040q在所设的情况下得证在所设的情况下得证352) )源电荷仍是点电荷源电荷仍是点电荷 取一闭合面不包围点电荷取一闭合面不包围点电荷(如图示如图示) 在闭合面上任取面元在闭合面上任取面元1Sd该面元对点电荷张的立体角该面元对点电荷张的立体角为为d2Sd也对应面元也对应面元两面元处对应的点电荷的电场强度分别为两面元处对应的点电荷的电场强度分别为21EE，2211SESEddd222201121044SrrqSrrqdd22022210114cos4cosrSqrS