第2章 平面问题的基础理论

1、第一节第一节 平面应力问题和平面应变问题平面应力问题和平面应变问题第二节第二节 平衡微分方程平衡微分方程第三节第三节 平面问题中一点的应力状态平面问题中一点的应力状态第四节第四节 几何方程几何方程 刚体位移刚体位移第五节第五节 物理方程物理方程第六节第六节 边界条件边界条件第二章 平面应力问题和平面应变问题第七节第七节 圣维南原理及其应用圣维南原理及其应用第八节第八节 按位移求解平面问题按位移求解平面问题第九节第九节 按应力求解平面问题按应力求解平面问题 相容方程相容方程第十节第十节 常应力情况下的简化常应力情况下的简化 应力函数应力函数第二章 平面应力问题和平面应变问题 弹弹性性力力学学平面

2、问题共有应力平面问题共有应力、应变应变和和位移位移8 8个未知函数个未知函数，且均为，且均为 。2-12-1平面应力问题和平面应变问题平面应力问题和平面应变问题 弹弹性性力力学学空间问题共有应力空间问题共有应力、应变应变和和位移位移1515个未知函数，且均为个未知函数，且均为 ；zyxf,yxf,平面应力第二章 平面应力问题和平面应变问题 （4 4）约束约束作用于板边，作用于板边，平行于板的中平行于板的中面，面，沿板厚不变沿板厚不变。 （3 3）面力面力作用于板边，作用于板边，平行于板的中平行于板的中面，面，沿板厚不变；沿板厚不变； （2 2）体力体力作用于作用于体内，平行于板的中体内，平行于

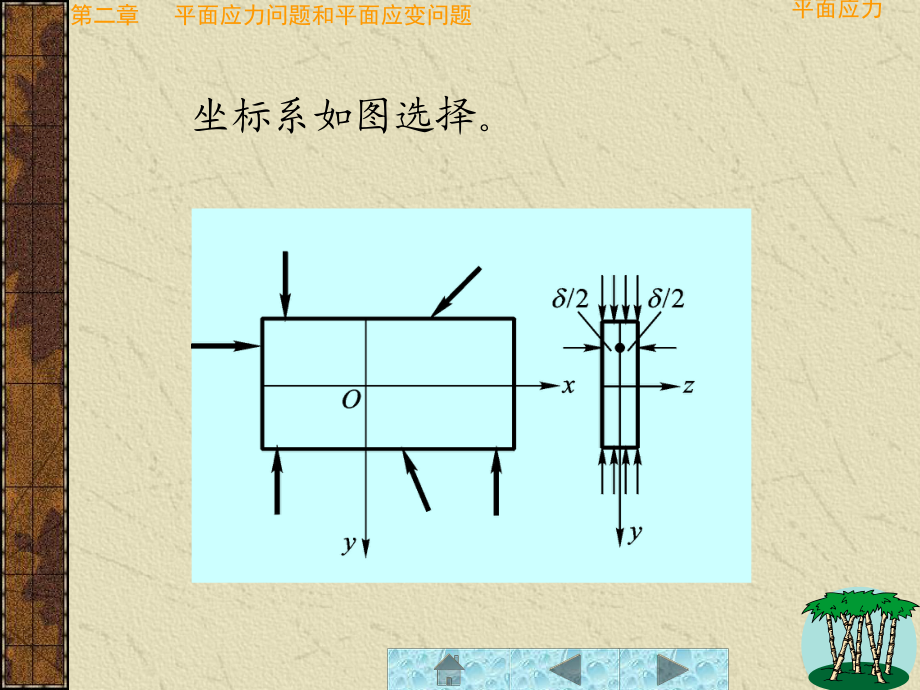
3、板的中面，面，沿板厚不变；沿板厚不变；条件是：条件是： 第一种：第一种：平面应力问题平面应力问题 平面应力 （1 1）等厚度的等厚度的薄板薄板；第二章 平面应力问题和平面应变问题 坐标系如图选择。平面应力第二章 平面应力问题和平面应变问题简化为平面简化为平面应力应力问题：问题： 故只有平面应力故只有平面应力 存在。存在。0,2zzyzxz(在V中) , 0,zyzxz 由于薄板很薄，应力是连续变化的，由于薄板很薄，应力是连续变化的，又无又无z向外力，可认为：向外力，可认为：平面应力（1 1）两板面上无面力和约束作用，两板面上无面力和约束作用，故故xyyx, ,第二章 平面应力问题和平面应变问题

4、 所以归纳为平面应力问题：所以归纳为平面应力问题：a.a.应力中只有平面应力应力中只有平面应力 存在；存在；b.b.且仅为且仅为 。yxf,平面应力xyyx, ,（2 2）由于板为等厚度，外力、约束沿）由于板为等厚度，外力、约束沿z z向向不变，故应力不变，故应力 仅为仅为 。yxf,xyyx, ,第二章 平面应力问题和平面应变问题如：弧形闸门闸墩计算简图：平面应力深梁计算简图：Fyfyf第二章 平面应力问题和平面应变问题因表面无任何面力，因表面无任何面力，0,0yxff 即：.0,zyzxz平面应力. 0,zyzxzAB例题例题1 1：试分析试分析ABAB薄层中的应力状态。薄层中的应力状态。

5、故接近平面应力问题。故接近平面应力问题。故表面上，有：故表面上，有：在近表面很薄一层内：在近表面很薄一层内：第二章 平面应力问题和平面应变问题 （2 2）体力体力作用于体内，平行于横截面，沿柱体作用于体内，平行于横截面，沿柱体长度方向不变；长度方向不变；平面应变第二种：平面应变问题第二种：平面应变问题条件是：条件是： （1 1）无限长的）无限长的等截面柱体等截面柱体； （3 3）面力面力作用于柱面，平行于横截面，沿柱作用于柱面，平行于横截面，沿柱体长度方向不变；体长度方向不变； （4 4）约束约束作用于柱面，平行于横截面，沿柱作用于柱面，平行于横截面，沿柱体长度方向不变。体长度方向不变。第二章

6、 平面应力问题和平面应变问题坐标系选择如图：平面应变oxzyozxy对称面zy第二章 平面应力问题和平面应变问题 故任何故任何z z 面（截面）均为对称面。面（截面）均为对称面。（平面位移问题）只有 ; , 0u,vw（平面应变问题）只有 ., , 0,0, 00 xyyxzyzxzyzxzw 平面应变（1 1）截面、外力、约束沿）截面、外力、约束沿z z 向不变，外力、约束向不变，外力、约束 平行平行xyxy面，柱体无限长；面，柱体无限长；简化为平面应变问题：简化为平面应变问题：第二章 平面应力问题和平面应变问题（2 2）由于）由于截面形状截面形状、体力体力、面力及约束沿面力及约束沿 向均不

7、变向均不变，故，故应力应力、应变应变和和位移均为位移均为 。yxf,z平面应变第二章 平面应力问题和平面应变问题 所以归纳为平面应变问题：所以归纳为平面应变问题： a.a.应变中应变中只有平面应变分量只有平面应变分量 存在；存在； b.b.且仅为且仅为 。平面应变yxf,xyyx,第二章 平面应力问题和平面应变问题例如：平面应变隧道挡土墙oyxyox第二章 平面应力问题和平面应变问题且仅为且仅为 。故只有故只有 ，本题中：本题中：0, 0zyzxz平面应变yxf,xyyx,oxyz例题例题2 2：试分析薄板中的应变状态。：试分析薄板中的应变状态。故为平面应变问题。故为平面应变问题。. 0,zy

8、zx第二章 平面应力问题和平面应变问题2 22 2平衡微分方程平衡微分方程定义 平衡微分方程平衡微分方程-表示物体内任一点的微分体的平衡条件。第二章 平面应力问题和平面应变问题 在任一点（x，y）取出一微小的平行六面体 ,作用于微分体上的力：体力：体力： 。1dd yxyxff ,定义应力：作用于各边上，应力：作用于各边上， 并表示出正面上并表示出正面上 由坐标增量引起由坐标增量引起 的的应力增量应力增量。第二章 平面应力问题和平面应变问题应用的基本假定应用的基本假定：连续性假定应力用连续函数来表示。小变形假定用变形前的尺寸代替变 形后的尺寸。 第二章 平面应力问题和平面应变问题列出平衡条件列

9、出平衡条件：合力 = 应力面积，体力体积； 以正向物理量来表示。平面问题中可列出3个平衡条件。平衡平衡条件条件第二章 平面应力问题和平面应变问题其中一阶微量抵消，并除以 得： .01dd1d1)dd(1d1)dd(, 0yxfxxyyyyxxFxyxyxyxxxxxyxdd0.(a)yxxxfxy0yF0 .(b)yxyyfyx，同理可得：平衡平衡条件条件第二章 平面应力问题和平面应变问题 , 0cM 当 时，得切应力互等定理,得,d21d21yyxxyxyxxyxy0d,dyx.(c)xyyx平衡平衡条件条件第二章 平面应力问题和平面应变问题 适用的条件-连续性，小变形；xy说明说明对平衡微

10、分方程的说明对平衡微分方程的说明： 代表A中所有点的平衡条件， 因位（ ，）A； 应力不能直接求出； 对两类平面问题的方程相同。第二章 平面应力问题和平面应变问题理论力学考虑整体 的平衡（只决定整体的运动状态）。 VVVd说明说明比较:材料力学考虑有限体 的平衡（近似）。 弹性力学考虑微分体 的平衡（精确）。第二章 平面应力问题和平面应变问题 当 均平衡时，保证 ， 平衡；反之则不然。 VV说明说明Vd 所以弹力的平衡条件是严格的，并且是精确的。 第二章 平面应力问题和平面应变问题理力（ V ）材力（ ）弹力（ ）bxhVd1dddyxVhV dxdy dx第二章 平面应力问题和平面应变问题思

11、考题思考题1.试检查，同一方程中的各项，其量纲 必然相同（可用来检验方程的正确性）。2.将条件 ,改为对某一角点的 ，将得出什么结果？3.微分体边上的应力若考虑为不均匀分布， 将得出什么结果？0cM0M第二章 平面应力问题和平面应变问题 已知坐标面上应力 ， 求斜面上的应力。问题的提出：2 23 3平面问题中一点的应力状态平面问题中一点的应力状态问题问题xyyx, ,第二章 平面应力问题和平面应变问题求解：取出一个三角形微分体（包含 面， 面， 面）， 边长).,(),(nnyxppppn.,mdsPAldsPBdsAB问题问题xy斜面应力表示：斜面应力表示：第二章 平面应力问题和平面应变问题

12、由平衡条件，并略去高阶分量体力项，得(1)求求（ , , ）(a a)xpyp,xyyyyxxxlmpmlp斜面应力斜面应力其中：其中：l=cos(n,x), m=cos(n,y)。第二章 平面应力问题和平面应变问题(2)求求（ ）将 向法向，切向投影，得nn ,),(yxppp22222, (b)() ().nxyxyxynyxyxxylpmpl mlmlpmplmlm斜面应力斜面应力第二章 平面应力问题和平面应变问题 设某一斜面为主面，则只有由此建立方程，求出:, 0,nn(3)求主应力求主应力斜面应力斜面应力. tan,222112221xyxyyxyx(c c)第二章 平面应力问题和平

13、面应变问题将x，y放在 方向，列出任一斜面上应力公式，可以得出（设 ）21, 21 . 45 ,2,2121的斜面上应力成发生在与主nmaxminnmaxmin(4)求最大，最小应力求最大，最小应力最大，最小应力最大，最小应力说明：以上均应用弹力符号规定导出。(d)第二章 平面应力问题和平面应变问题几何方程几何方程表示任一点的微分线段 上形变与位移之间的关系。2 24 4几何方程刚体位移几何方程刚体位移定义定义第二章 平面应力问题和平面应变问题变形前位置： 变形后位置： 各点的位置如图。 通过点P(x,y)作两正坐标向的正坐标向的微分线段, ,dyPBdxPA, , ,P A B定义定义,P

14、A B第二章 平面应力问题和平面应变问题32sin,3!cos11,2 !tan. 应用基本假定：连续性；小变形。当很小时，假定假定第二章 平面应力问题和平面应变问题().xuudxuuxdxx.yvy假定假定由位移求形变：PA 线应变PA 转角PB 线应变PB 转角同理，tan.vdxvxdxxyu第二章 平面应力问题和平面应变问题 适用于区域内任何点，因为（x,y） A；对几何方程的说明：. , ,yuxvyvxuxyyx所以平面问题的几何方程平面问题的几何方程为：说明说明 适用条件：a.连续性；b.小变形。 应用小变形假定，略去了高阶小量 线性的几何方程；第二章 平面应力问题和平面应变问

15、题 几何方程是变形后物体连续性条件 的反映和必然结果。 形变和位移之间的关系： 位移确定位移确定 形变完全确定：形变完全确定： 从物理概念看，各点的位置确定，则微分线段上的形变确定 。 说明说明 从数学推导看，位移函数确定，则其导数（形变）确定 。第二章 平面应力问题和平面应变问题 从物理概念看， ， 确定，物体还可作刚体位移。 从数学推导看， ， 确定，求位移是积分运算，出现待定函数。形变确定，位移不完全确定形变确定，位移不完全确定： 形变与位移的关系形变与位移的关系第二章 平面应力问题和平面应变问题由 ,两边对y积分，由 ,两边对x积分，例：若例：若 , ,求位移：求位移：0 xyyx0,

16、 (a)xyvuxy形变与位移的关系形变与位移的关系0 xxu0yyv).(0),(1yfyxu).(0),(2xfyxv代入第三式第二章 平面应力问题和平面应变问题分开变量， 12d ( )d( ) ( ).(b)ddfyfxyx 因为几何方程第三式对任意的（x，y）均应满足。当x（y）变化时，式(b)的左，右均应=常数 ，由此解出 。可得形变与位移的关系形变与位移的关系21, ff , . (c)oou uyv vx 第二章 平面应力问题和平面应变问题物理意义：00,vu形变与位移的关系形变与位移的关系表示物体绕原点的刚体转动。表示x，y向的刚体平移，第二章 平面应力问题和平面应变问题结论

17、结论 形变确定，则形变确定，则与形变有关的位移可以与形变有关的位移可以确定，而与形变无关的刚体位移确定，而与形变无关的刚体位移则未定。则未定。须通过边界上的约束条件来确定 。,oovu,oovu第二章 平面应力问题和平面应变问题思考题思考题1.试证明微分体绕z轴的平均转动分量是).(21yuxv,cbaxyyx2.当应变为常量时， 试求出对应的位移分量。第二章 平面应力问题和平面应变问题物理方程表示（微分体上）应力和形变 之间的物理关系。11(), ,11(), ,11(), .xxyzyzyzyyzxzxzxzzxyxyxyEGEGEG定义即为广义胡克定律：2 25 5物理方程物理方程第二章

18、 平面应力问题和平面应变问题物理方程的说明物理方程的说明：说明说明 正应力只与线应变有关；切应力只与切 应变有关。 是线性的代数方程； 是总结实验规律得出的； 适用条件理想弹性体；第二章 平面应力问题和平面应变问题 物理方程的两种形式：物理方程的两种形式： 应变用应力表示，用于 按应力求解； 应力用应变（再用位移表示） 表示，用于按位移求解。)(f)(f说明说明第二章 平面应力问题和平面应变问题平面应力问题的物理方程：平面应力问题的物理方程： 代入 ，得：在z方向0zyzxz11(), (),(a)2(1).xxyyyxxyxyEEE).( , 0yxzzE平面应力第二章 平面应力问题和平面应

19、变问题 代入 得, 0zyzxz221(),11(),(b)12(1).xxyyyxxyxyEEE平面应变问题的物理方程平面应变问题的物理方程平面应变在z方向，).(,0yxzz第二章 平面应力问题和平面应变问题平面应力物理方程平面应变物理方程：.1 ,12EE变换关系变换关系：.1 ,)1()21(2EE平面应变物理方程平面应力物理方程：第二章 平面应力问题和平面应变问题思考题 1.试证：由主应力可以求出主应变，且两者方向一致。 2.试证：3个主应力均为压应力，有时可以产生拉裂现象。 3.试证：在自重作用下，圆环（平面应力问题）比圆筒（平面应变问题）的变形大。第二章 平面应力问题和平面应变问

20、题 位移边界条件位移边界条件 设在 部分边界上给定位移分量 和 ,则有),()( ),()(svvsuuss（在 上)。（a）usus定义)(su)( sv 边界条件边界条件 表示在边界上位移与约束，或应力与面力之间的关系。位移边界条件26边界条件第二章 平面应力问题和平面应变问题 若为简单的固定边， 则有位移边界条件的说明：sus, 0 vu, 0)( , 0)(ssvuus（在 上）。（b） 它是在边界上物体保持连续性的条 件，或位移保持连续性的条件。 它是函数方程，要求在 上每一点 ， 位移与对应的约束位移相等。第二章 平面应力问题和平面应变问题在23 中，通过三角形微分体的平衡条件，导

21、出坐标面应力与斜面应力的关系式，应力边界条件应力边界条件设在 上给定了面力分 量 , ,xyyyyxxxlmpmlp).( ),(sfsfyxs（在A中）。（c）应力边界条件第二章 平面应力问题和平面应变问题将此三角形移到边界上，并使斜面与边界面重合，则得应力边界条件:()( ), . (d)()( ),xyxsxyxysylmfssmlfs（在 上）第二章 平面应力问题和平面应变问题 它是边界上微分体的静力平衡条件；说明应力边界条件的说明： 式（c）在A中每一点均成立，而 式（d）只能在边界 s上成立； 它是函数方程，要求在边界上每一点s 上均满足，这是精确的条件；第二章 平面应力问题和平面

22、应变问题 所有边界均应满足，无面力的边界 （自由边） 也必须满足。 式（d）中， 按应力符号规定， ， 按面力符号规定；yfxf 位移,应力边界条件均为每个边界两 个，分别表示 ， 向的条件；, 0yxffxy说明xyyx, ,第二章 平面应力问题和平面应变问题若x=a为正x 面，l = 1, m = 0, 则式(d)成为( ), (). (e)x ax x axxyyff当边界面为坐标面时当边界面为坐标面时，坐标面yxbaxfyfxxfyfxyxxy第二章 平面应力问题和平面应变问题若x=-b为负x 面，l = -1, m = 0 , 则式(d)成为( ), (). (f)xbx xbxxy

23、yffyxbaxfyfxxfyfxyxxy第二章 平面应力问题和平面应变问题应力边界条件的两种表达式：应力边界条件的两种表达式：两种表达式 在同一边界面上，应力分量应等于对 应的面力分量（数值相等，方向一 致）。即在同一边界面上,应力数值应 等于面力数值(给定),应力方向应同面 力方向(给定)。 在边界点取出微分体，考虑其平衡条 件，得式（d）或（e），（f ）；第二章 平面应力问题和平面应变问题 在斜面上， 在坐标面上，由于应力与面力的符号规定不同，故式（e），（f ）有区别。例如：.)( ,)(yyxsxfpfps两种表达式第二章 平面应力问题和平面应变问题lh/2h/2qyxoyyxxy

24、yyxx例1 列出边界条件：1q第二章 平面应力问题和平面应变问题0( )0 ( )0.x 0 x 0 x,u,v边界( )0, ()0.x x lxy x lxl,边界( ) ( )0.yhyxhyy22xhy,q ,2l边 界1( )0, ( ).yhyxhyy22hy,q2边 界第二章 平面应力问题和平面应变问题yxoqqqqbbaa例2 列出边界条件：xyyyxx第二章 平面应力问题和平面应变问题显然，边界条件要求在 上， 也成抛物线分布。b()0, ()0.yyyxybyb 边界：axx2()( ) , ()0.x xaxy xaxayqb边界：第二章 平面应力问题和平面应变问题 部

25、分边界上为位移边界条件，另一部分边界上为应力边界条件；混合边界条件混合边界条件：混合边界条件： 同一边界上，一个为位移边界条件，另一个为应力边界条件。第二章 平面应力问题和平面应变问题例3 列出 的边界条件：ax .0)(,0)(,axxyaxuaxyxoa第二章 平面应力问题和平面应变问题思考题 oxy(c)(a)(d)(b)qxnyABAxyoAMygn第二章 平面应力问题和平面应变问题1.若在斜边界面上，受有常量的法向分布 压力 作用，试列出应力边界条件， (思考题图中（a）)。2.证明在无面力作用的0A边上， 不等 于零（思考题图中(b)）。3.证明在凸角A点附近，当无面力作用 时，其

26、应力为零（思考题图中 (c)）。qy第二章 平面应力问题和平面应变问题4.试导出在无面力作用时，AB边界上的 之间的关系。 （思考题图中（d）。5.试比较平面应力问题和平面应变问题的 基本方程和边界条件的异同，并进一步 说明它们的解答的异同。xyyx, ,第二章 平面应力问题和平面应变问题 弹性力学问题是微分方程的边值问题。应力，形变，位移等未知函数必须满足A内的方程和S上的边界条件。主要的困难在于难以满足边界条件。 27圣维南原理及其应用 圣维南原理圣维南原理可用于简化小边界上的应力边界条件。第二章 平面应力问题和平面应变问题 如果把物体的一小部分边界上的面力，变换为分布不同但静力等效的面力

27、（主矢量相同，对同一点的主矩也相同），那么，近处的应力分量将有显著的改变，但远处所受的影响可以不计。圣维南原理圣维南原理：圣维南原理：第二章 平面应力问题和平面应变问题圣维南原理1.圣维南原理只能应用于一小部分边界 （小边界，次要边界或局部边界）；圣维南原理的说明：圣维南原理的说明：4.远处 指“近处”之外。3.近处 指面力变换范围的一，二倍 的局部区域；2.静力等效 指两者主矢量相同，对 同一点主矩也相同；第二章 平面应力问题和平面应变问题圣维南原理 圣维南原理表明，在小边界小边界上进行面力的静力等效变换后，只影响近处（局部近处（局部区域）区域）的应力，对绝大部分弹性体区域的应力没有明显影响

28、。 圣维南原理推广：如果物体一小部分边界上的面力是一个平衡力系（主矢量及主矩都等于零），那么，这个面力就只会使近处产生显著的应力，而远处的应力可以不计。第二章 平面应力问题和平面应变问题例1 比较下列问题的应力解答：hFF/2 F/2F/2F/2FF/b3465421321 )(bh 6543214321 b第二章 平面应力问题和平面应变问题例2 比较下列问题的应力解答：推广0 0 0 03412 0 02 01第二章 平面应力问题和平面应变问题 圣维南原理的应用：圣维南原理的应用：1.推广解答的应用；2.简化小边界上的边界条件。应用第二章 平面应力问题和平面应变问题圣维南原理在小边界上的应用

29、：圣维南原理在小边界上的应用：lx 精确的应力边界条件如图，考虑 小边界，第二章 平面应力问题和平面应变问题 上式是函数方程，要求在边界上任一点，应力与面力数值相等，方向一致，往往难以满足。)(),(),(),(yfyxyfyxylxxyxlxx(a)在边界 上，lx 第二章 平面应力问题和平面应变问题 在小边界x=l上，用下列条件代替式(a)的条件： 在同一边界在同一边界 x=l 上，上， 应力的主矢量 = = 面力的主矢量（给定); 应力的主矩(M) = = 面力的主矩（给定）.),(yxFF数值相等,方向一致.(b)圣维南原理圣维南原理的应用的应用积分的应力边界条件积分的应力边界条件第二

30、章 平面应力问题和平面应变问题 右端面力的主矢量，主矩的数值及方向，均已给定； 左端应力的主矢量，主矩的数值及方向，应与面力相同，并按应力的方向规定确定正负号。第二章 平面应力问题和平面应变问题具体列出具体列出3 3个积分的条件：个积分的条件：)( 1)(1)()(1)(1)()( 1)(1)(2/2/2/2/2/2/2/2/2/2/2/2/ShhylxhhxyhhxlxhhxNhhxlxhhxFdyyfdyMydyyfydyFdyyfdy第二章 平面应力问题和平面应变问题即： 应力的主矢量，主矩的数值=面力的主矢量，主矩的数值； 应力的主矢量，主矩的方向=面力的主矢量，主矩的方向。 式中应力

31、主矢量，主矩的正方向应力主矢量，主矩的正方向,正负号正负号的确定： 应力的主矢量的正方向，即应力的正方向， 应力的主矩的正方向，即（正应力） （正的矩臂）的方向。第二章 平面应力问题和平面应变问题讨论：讨论： 1.如果只给出面力的主矢量，主矩如图，则式(c)右边直接代入面力的主矢量，主矩； 2.在负 x 面， ，由于应力，面力的符号规定不同，应在式(c)中右端取负号； 3.积分的应力边界条件(b)或(c)虽是近似的，但只用于小边界，不影响整体解答的精度。lx第二章 平面应力问题和平面应变问题 精确的应力边界条件精确的应力边界条件 积分的应力边界条件积分的应力边界条件方程个数方程个数 2 3方程

32、性质方程性质 函数方程（难满足）函数方程（难满足） 代数方程（易满足）代数方程（易满足）精确性精确性 精确精确 近似近似适用边界适用边界 大，小边界大，小边界 小边界小边界比较：比较：第二章 平面应力问题和平面应变问题思考题思考题1、为什么在大边界（主要边界）上，不能 应用圣维南原理？2、试列出负 面上积分的应力边界条件， 设有各种面力作用，或面力的主矢量和主矩作用。x第二章 平面应力问题和平面应变问题 平面应力问题与平面应变问题，除物理方程的弹性系数须变换外，其余完全相同。因此，两者的解答相似,只须将 进行变换。以下讨论平面应力问题平面应力问题。1.1.平面问题的基本方程及边界条件平面问题的

33、基本方程及边界条件,E平面问题2 28 8按位移求解平面问题按位移求解平面问题第二章 平面应力问题和平面应变问题 平面应力问题0,0.yxxxyxyyfxyfyx 平面域平面域A内的基本方程内的基本方程: :平衡微分方程（在（在A内）内）第二章 平面应力问题和平面应变问题, , .xyxyuvvuxyxy11(),(),2(1).xxyyyxxyxyEEE几何方程物理方程（在（在A内）内）（在（在A内）内）第二章 平面应力问题和平面应变问题应力边界条件 位移边界条件 （在 上）（在 上）(),().xyxsxyxysylmfmlfs),(vuxyyxxyyxus(),().ssuuvvS上边界

34、条件上边界条件: 8个未知函数 必须满足上述方程和边界条件。第二章 平面应力问题和平面应变问题 按位移求解按位移求解（位移法）取 ， 为基本未知函数，从方程和边界条件中消去形变和应力，导出只含 ， 的方程和边界条件，从而求出 ， ；再求形变和应力。2.2.解法解法消元法消元法 uvuvu v解法第二章 平面应力问题和平面应变问题 按应力求解按应力求解（应力法）取 为基本未知函数，从方程和边界条件中消去位移和形变，导出只含应力的方程和边界条件，从而求出应力；再求形变和位移。xyyx, 这是弹力问题的两种基本解法这是弹力问题的两种基本解法。第二章 平面应力问题和平面应变问题3. 按位移求解按位移求

35、解uvu vu vu v 将其他未知函数用 ，表示： 形变用 ，表示几何方程; 应力先用形变来表示（物理方程）， 再代入几何方程，用 ，表示: 取 ， 为基本未知函数；按位移求解第二章 平面应力问题和平面应变问题2222()(),11()(),(a)11().2(1)2(1)xxyyyxxyxyEEuvxyEEvuyxEEvuxy第二章 平面应力问题和平面应变问题 在A中导出求 ，的基本方程将式(a) 代入平衡微分方程，22222222222211()0,122( ) (b)11()0.122xyEuuvfxyx yAEvvufyxx y u vu v上式是用 ，表示的平衡微分方程。第二章 平

36、面应力问题和平面应变问题位移边界条件 （在 上）(d)（在 上）(c).)(,)(vvuussus.)(21)(1,)(21)(122ysxsfyuxvlxuyvmEfxvyumyvxulEs应力边界条件将式(a)代入应力边界条件， 在在S S上的边界条件上的边界条件第二章 平面应力问题和平面应变问题 按位移求解时，按位移求解时， ， 必须满足必须满足A A内的方程内的方程( (b b) )和边界条件和边界条件( (c c) )，( (d d) )。u vuvuv归纳：归纳：式(b)，(c)，(d)是求解 ， 的条件;也是校核 ， 是否正确的全部条件。第二章 平面应力问题和平面应变问题 按位移

37、求解（位移法）的优缺点：按位移求解（位移法）的优缺点： 求函数式解答困难，但在近似解法（变分法，差分法，有限单元法）中有着广泛的应用。 适用性广可适用于任何边界条件。第二章 平面应力问题和平面应变问题例1 考虑两端固定的一维杆件。图(a)，只受重力作用， 。试用位移法求解。gffyx , 0 xoyloyxgg(a) (b)第二章 平面应力问题和平面应变问题解：为了简化，设位移 按位移求解，位移应满足式(b),(c),(d)。代入式(b),第一式自然满足，第二式成为, 0).(, 0yvvu.2222Egdyvdyvxoyloyxgg (a) (b)第二章 平面应力问题和平面应变问题 均属于位

38、移边界条件，代入 ，.22BAyyEgvly, 00( )0,yv0;B v得得( )0,y lv.2gAlE解出第二章 平面应力问题和平面应变问题).2(2),2(2),(22ylgylEgylyEgvyy在 处，2ly . 0y代入 ，并求出形变和应力，v第二章 平面应力问题和平面应变问题思考题试用位移法求解图(b)的位移和应力。第二章 平面应力问题和平面应变问题（1）取 为基本未知函数；基本方程xyyx,29 按应力求解平面问题按应力求解平面问题相容方程相容方程1.按应力求解平面应力问题按应力求解平面应力问题（2）其他未知函数用应力来表示:第二章 平面应力问题和平面应变问题 位移用形变应

39、力表示，须通过积分，不仅表达式较复杂，而且包含积分带来的未知项，因此位移边界条件用应力分量来表示时既复杂又难以求解。故在按应力求解时在按应力求解时，只考虑全部为应力边界条件的问题只考虑全部为应力边界条件的问题, ,即 。 形变用应力表示（物理方程）。)0,(usss按应力求解第二章 平面应力问题和平面应变问题 在A内求解应力的方程.22222yxxyxyyxvu(b) 从几何方程中消去位移 ， ，得相容方相容方程（形变协调条件）程（形变协调条件）： 补充方程从几何方程，物理方程中消去位移和形变得出 :平衡微分方程 （2个）。 (a)第二章 平面应力问题和平面应变问题 代入物理方程，消去形变，并

40、应用平衡微分方程进行简化，便得用应力表示的相容方程 ： 2()(1)(),(c)yxxyffxy .22222yx其中 (4) 应力边界条件假定全部边界上均为应力边界条件 。)0,(usss第二章 平面应力问题和平面应变问题（1）A内的平衡微分方程；（2）A内的相容方程；（3）边界 上的应力边界条件；（4）对于多连体，还须满足位移的单值条 件（见第四章）。 归纳归纳：xyyx,ss （1）-（4）也是校核应力分量是否正确的全部条件。 按应力求解平面应力问题按应力求解平面应力问题 ，应力 必须满足下列条件：第二章 平面应力问题和平面应变问题2.形变协调条件（相容方程）的物理意义形变协调对应的位移

41、存在位移必然连续；形变不协调对应的位移不存在不是物体实际存在的形变微分体变形后不保持连续。 形变协调条件是与形变对应的位移存在且连续的必要条件。 形变协调条件是位移连续性的必然结果。连续体位移连续几何方程形变协调条件。第二章 平面应力问题和平面应变问题点共点（连续），变形后三连杆在 点共点，则三连杆的应变必须满足一定的协调条件。例1 三连杆系统，由于物体是连续的，变形前三连杆在 DD FDD第二章 平面应力问题和平面应变问题1.试比较按位移求解的方法和按应力求解的 方法，并与结构力学中的位移法和力法作 比较。2.若 是否可能 成为弹性体中的形变？3.若 是否 可能为弹性体中的应力？,)(,22

42、xybabxayxyyx, 0, 022xyyxyxbyaxff思考题思考题第二章 平面应力问题和平面应变问题 相容方程 (A) (a)1.常体力情况下按应力求解的条件常体力情况下按应力求解的条件0)(2yx0,0yxyyxyxxfxyfyx(A) (b) 平衡微分方程 按应力函数求解2 21010常体力情况下的简化常体力情况下的简化 应力函数应力函数第二章 平面应力问题和平面应变问题 应力边界条件 ss .)( ,)(ysxyyxsyxxflmfml(S) (c)0,(usss 多连体中的位移单值条件。 (d)第二章 平面应力问题和平面应变问题 在 - - 条件下求解 的全部条件(a)，(b

43、)，(c)中均不包含弹性常数，故 与弹性常数无关。2.在常体力在常体力, ,单连体单连体, ,全部为应力边全部为应力边界条件（界条件（ ）下的应力）下的应力 特征：特征：ss xyyx,xyyx,xyyx,第二章 平面应力问题和平面应变问题结论：结论：不同材料的应力( )的理论解相 同，用试验方法求应力时，也可以用不 同的材料来代替。xyyx,两类平面问题的应力解 相同，试 验时可用平面应力的模型代替平面应变的 模型。 xyyx,第二章 平面应力问题和平面应变问题 3.常体力下按应力求解的简化常体力下按应力求解的简化, , 0. (e)xxyyxyf xf y 22222, , . (f)xy

44、xyyxx y 对应的齐次微分方程的通解通解，艾里已求出为 非齐次微分方程(b)的任一特解特解，如取（1）常体力下平衡微分方程的通解通解是： 非齐次特解非齐次特解+ +齐次通解。齐次通解。第二章 平面应力问题和平面应变问题齐次微分方程的通解通解的求解过程：的求解过程： 将上式齐次微分方程的前一式写为： 00 xyyxxyyxyx)(xyxyx第二章 平面应力问题和平面应变问题根据微分方程理论，这就一定存在某一函数 ，使得yAx),(yxAxAxy同样，将上式齐次微分方程的后一式写为： )(xyyxy第二章 平面应力问题和平面应变问题根据微分方程理论，这就一定存在某一函数 ，使得xBy),(yx

45、ByBxy即有：yBxA第二章 平面应力问题和平面应变问题因而，又一定存在某一函数 ，使得yA),(yxxB即有通解：22222, , . (f)xyxyyxx y 第二章 平面应力问题和平面应变问题. yxy,fxx,fy2xyy22yx22x所以满足平衡微分方程的通解为平衡微分方程的通解为: :(g)为艾里应力函数。第二章 平面应力问题和平面应变问题如果，则A，B均可用一个函数表示，即说明：说明：).()(xfyyfx),()(ByAx. ,xfByfAa.导出艾里（Airy）应力函数 ，是应用偏导数的相容性，即第二章 平面应力问题和平面应变问题d. 由 再去求应力（式（g）,必然满足平衡

46、微分方程，故不必再进行校核。c. 仍然是未知的。但已将按应力 求解转变为按应力函数 求解，从3个未知函数减少至1个未知函数 。b.导出应力函数 的过程，也就证明了 的存在性，故可以用各种方法去求解 。),(yx),(xyyx第二章 平面应力问题和平面应变问题（2）应力应满足相容方程（a），将式 （g）代入（a），得 2240. (h) ss （3）若全部为应力边界条件（ ）， 则应力边界条件也可用 表示。第二章 平面应力问题和平面应变问题归纳：归纳：（1）A内相容方程（h）；（2） 上的应力边界条件；（3）多连体中的位移单值条件连体。ss 求出 后，可由式（g）求得应力。 在常体力下求解平面问

47、题 ，可转变为按应力函数按应力函数 求解求解， 应满足:第二章 平面应力问题和平面应变问题1，在常体力，单连体和全部为应力边界条件条件下，对于不同材料和两类平面问题的， 和均相同。试问其余的应力分量，应变和位移是否相同？xyxy思考题第二章 平面应力问题和平面应变问题2，对于按位移(u, v)求解，按应力（ ， ， ）求解和按应力函数 求解的方法，试比较其未知函数，应满足的方程和条件，求解的难易程度及局限性。xyxy第二章 平面应力问题和平面应变问题 1例题2例题3例题4例题7例题5例题6例题第二章 平面应力问题和平面应变问题例1 试列出图中的边界条件。SFMFyxl h/2 h/2q2)(l

48、xq1q) 1,(hl(a)第二章 平面应力问题和平面应变问题解: (a)在主要边界 应精确满足下列边界条件：. , 0 , 2/; 0 ,)( , 2/12qhylxqhyxyyxyy2/hy第二章 平面应力问题和平面应变问题在小边界x = 0应用圣维南原理，列出三个积分的近似边界条件，当板厚 时，1。sxhhxyxhhxxhhxFyMyyFyd)(,d)(,d)(02/2/02/2/02/2/第二章 平面应力问题和平面应变问题在小边界x = l，当平衡微分方程和其它各边界条件都已满足的条件下，3个积分的边界条件必然满足，可以不必校核。第二章 平面应力问题和平面应变问题(b) 在主要边界x=

49、 0, b，应精确满足下列边界条件：。qlxgyxxyxxyx , 0 ; 0 , 0030FOxyqh(b)gy b/2 b/2) 1,(bh第二章 平面应力问题和平面应变问题 在小边界y = 0，列出3个积分的边界条件，当板厚 时，1。2d)(,43d)(,23d)(000000FxbFxxFxybyxybyyby第二章 平面应力问题和平面应变问题 注意在列力矩的条件时两边均是对原点o 的力矩来计算的。 对于y = h的小边界可以不必校核。第二章 平面应力问题和平面应变问题例例2 2 厚度 悬臂梁，受一端的集中力F的作用。已求得其位移的解答是 试检查此组位移是否是图示问题的解答。1。EIF

50、lEIFxlEIFxEIFxyvyIGFhEIFlIGFyEIFyEIyFxu3262,)82(662323222332第二章 平面应力问题和平面应变问题 h/2 h/2AxylFO) 1,(hl第二章 平面应力问题和平面应变问题解： 此组位移解答若为图示问题的解答，则应满足下列条件:(1) 区域内用位移表示的平衡微分方程 (书中式218）;第二章 平面应力问题和平面应变问题（2）应力边界条件（书中式219），在 所有受面力的边界 上。其中在小边 界上可以应用圣维南原理，用3个积 分的边界条件来代替。（3）位移边界条件（书中式214）。本 题在x = l的小边界上，已考虑利用圣 维南原理，使3

51、个积分的应力边界条 件已经满足。S第二章 平面应力问题和平面应变问题 因此，只需校核下列三个刚体的约束条件： A点（ x = l及y = 0），.0),(xuvu 读者可校核这组位移是否满足上述条件，如满足，则是该问题之解。第二章 平面应力问题和平面应变问题。CxycCxyyBxAybDyCByAxyaxyyxxyyxxyyx , 0 )(; , , )(; , , )(2223例例3 3 试考虑下列平面问题的应变分量是否可能存在第二章 平面应力问题和平面应变问题解：应变分量存在的必要条件是满足形变 相容条件，即 （a）相容； （b）须满足B = 0, 2A=C ； （c）不相容。只有C =

52、0，则.22222yxxyxyyx第二章 平面应力问题和平面应变问题2222( ) , , ;( ) (), (), ;xyxyxyxyaAx ByCx DyEx FybA xyB xyCxy例例4 4 在无体力情况下，试考虑下列应力分量是否可能在弹性体中存在：第二章 平面应力问题和平面应变问题解：弹性体中的应力，在单连体中必须 满足： （1）平衡微分方程； （2）相容方程； （3）应力边界条件（当 ）。SS第二章 平面应力问题和平面应变问题（a）此组应力满足相容方程。为了满足平 衡微分方程，必须A=-F, D=-E.此外，还应满足应力边界条件。（b）为了满足相容方程，其系数必须满足 A +

53、B = 0。 为了满足平衡微分方程，其系数必须 满足 A = B =-C/2。 上两式是矛盾的，因此此组应力分量 不可能存在。第二章 平面应力问题和平面应变问题例例5 5 若 是平面调和函数，即满足拉普拉斯方程 试证明函数 都满足重调和方程，因而都可以作为应力函数使用。. 02 ffyxyfxff) ( , , ,22),( yxf40,第二章 平面应力问题和平面应变问题解： 上述函数作为应力函数，均能满足相 容方程（重调和方程），.04 第二章 平面应力问题和平面应变问题。xChqxyCyCyhqyyxhqxyy2),46(a)例例6 6 图中的梁，受到如图所示的荷载的作用，试用下列应力表达式求解其应力，第二章 平面应力问题和平面应变问题202qh)202(22qhqlxy) 1,(hlloqql h/2 h/2第二章 平面应力问题和平面应变问题解：本题是按应力求解的，在应力法中，应力分量在单连体中必须满足（1）平衡微分方程；（2）相容方程 ;（3）应力边界条件（在 ）。 将应力分量（a）代入平衡微分方程和相容方程，两者都能满足。0)(2yxSS第二章 平面应力问题和平面应变问题再校核边界条件，在主要边界上，21316, 0, ()0,