工程制图考试攻略

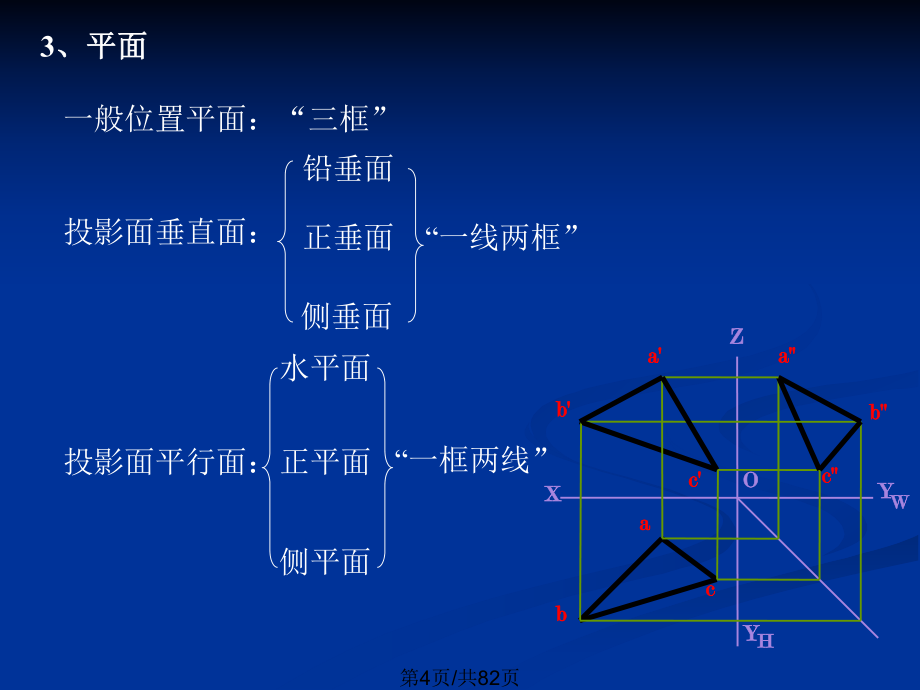
1、会计学1工程制图考试攻略工程制图考试攻略第1页/共82页一、点线面一、点线面（一）点线面对投影面的相对位置（一）点线面对投影面的相对位置1、点点坐标 X空间点到W面的距离Y空间点到V面的距离Z空间点到H面的距离作图规律作图规律a aOaxYHa azXZYW特殊点：投影面上、投影轴上特殊点：投影面上、投影轴上第2页/共82页2、直线、直线a aa ab bb bbbaaHHY YZ ZX Xo oWWY Y一般位置直线：“三斜”直角三角形法直角三角形法实长投影长距离差倾角投影面平行线：水平线正平线侧平线“一斜二平”投影面垂直线：铅垂线正垂线侧垂线“一点二平”第3页/共82页3、平面、平面b b

2、a ac cX XY YZ ZO OHHY YWWaabbc ca ab bc c一般位置平面：“三框”投影面垂直面：“一线两框”铅垂面正垂面侧垂面投影面平行面：水平面正平面侧平面“一框两线”第4页/共82页（二）点、线、面相互位置（二）点、线、面相互位置4、点、点、点、点两点两点 X Y Z重影点重影点不在一直线上的三点构成平面不在一直线上的三点构成平面a aa aX XY YHHZ ZY YWWb bb ba(b)a(b)Z ZA AZ ZB Bb bb bb ba aX XY YHHZ ZY YWWa aa aX XY YZ Z两点之间的距离两点之间的距离第5页/共82页5、点、线、点、

3、线（1）点在直线上）点在直线上从属性定比性（2）点不在直线上）点不在直线上直线与直线外一点构成平面点到直线的距离第6页/共82页6、点、面、点、面（1）点在平面上：在平面上取点）点在平面上：在平面上取点（2）点不在平面上：距离）点不在平面上：距离7、直线、直线、直线、直线（1）平行两直线）平行两直线a a b bd dc cX XO Oa ab bd dc cX XO OY YY YZ ZWWHHe ee ef ff fm mm mn nn ne ef fmmnn平行直线表示平面第7页/共82页（2）相交直线）相交直线X XO Oa ab ba ab bc cd dc cd dk kk ka

4、ab ba aaabbb bX XO OY YY YZ ZWWHHc cd dc cd dc cdd g g(j (j) )c cd dd dc cb ba aa ab bO OX Xg gj je e(f)(f)e ef f相交直线表示平面（3）交叉直线）交叉直线第8页/共82页（4）垂直直线）垂直直线（相交不垂直）（相交不垂直）c cd dd dc cX XO Oa aa ab bb bc cO OX Xa ab ba ab bd dc cd da ab ba ab bd dc cc cd dX XO Oa ab ba ab bX XO Oc cd dc cd d（交叉垂直交叉垂直）（交叉

5、垂直）（交叉垂直）（相交垂直）（相交垂直）（交叉垂直）（交叉垂直）（相交垂直）（相交垂直）d dc cc cd da aa ab bb bX XO Oa aab b b bc cd dc c(d)(d)X XO OX XO Oc cc cb bb ba aa ac c1 1b b1 1(c)(c)(b)(b)第9页/共82页8、线、面、线、面（1）直线在平面：在平面上取线）直线在平面：在平面上取线（2）直线不在平面上）直线不在平面上（a）平行（b）相交X XO Oc cd de ec ce ed da ab bk kk kb ba an nm ma ab bc cb ba ac cm mn n

6、e ed dd de ek kk k3 3(4 )(4 )3 34 4P PHH重影点重影点X XO O（k k）f ff fe ee ec cd dd dC Ck k重影点重影点a ab ba(b)a(b)n n（m m）m m（n n）第10页/共82页（c）垂直d dd de ee ea ab bc ca ab bc cO OX Xk km mm mk kMKMK ABCABC（9）面、面）面、面X XO Oc cf fc cf fb be ea ad da ad de eb b两平面平行两平面平行（a）平行（b）相交a ab bc cX XO Op pHHp pc cb ba am m

7、m mn nn n不可见不可见可见可见第11页/共82页（c）垂直（10）投影变换）投影变换新轴的建立新轴的建立作图规律作图规律X XO Oa ac cb bb bc ca aMNMN ABC ABC平面平面P P ABC ABCe ee eX XO Od dd dn nm mp pm mp pn nMNMN ABC ABC平面平面P P ABC ABC第12页/共82页二、基本体及其截交二、基本体及其截交1、棱柱体（一）平面立体（一）平面立体2、棱锥体3、4、5、6平面立体的棱线与平面的截交点平面立体的棱线与平面的截交点（二）曲面立体（二）曲面立体1、圆柱体：3种2、圆锥体：5种3、圆球：1

8、种第13页/共82页三、立体相交三、立体相交1、平面立体与平面立体相交、平面立体与平面立体相交参与相交的立体的棱线与另一个立体的贯穿点参与相交的立体的棱线与另一个立体的贯穿点同坡屋面同坡屋面2、平面立体与曲面立体相交、平面立体与曲面立体相交平面立体的棱面截曲面立体的截交线平面立体的棱面截曲面立体的截交线3、曲面立体与曲面立体相交、曲面立体与曲面立体相交特殊点与一般点连成封闭空间曲线特殊点与一般点连成封闭空间曲线第14页/共82页四、轴测投影四、轴测投影测正连斜测正连斜五、组合体五、组合体形体分析法形体分析法线面分析法线面分析法第15页/共82页例例1 过过A作直线作直线AB与与CD相交，交点相

9、交，交点K距距H面为面为20，线，线段段AB长为长为50，求作，求作AB的投影。的投影。2. 2. 用直角三角形法求用直角三角形法求 出出AKAK的实长。的实长。3. 3. 用等比性按用等比性按ABAB的实的实 长求出长求出B B点的投影。点的投影。2020b bb ba ac cd dc cd dX Xa aABAB实长实长=50=50k kk k1. 1. 在在OXOX轴上方距轴上方距OXOX轴轴 为为2020作一水平线，作一水平线， 与与c d c d 交于交于k k ，向，向 下求出下求出k.k.第16页/共82页c cd dc cd da aa ae ef fe ef fb bb b

10、 例例2 2 过点过点A作线作线AB EF，问问AB与与CD是否相交。是否相交。 因因G点和点和H点分属点分属CD和和AB，不不是公有点，因此是公有点，因此AB与与CD两直线两直线不相交。不相交。g g (h )(h )h hg g作图：作图： 作作ababef ef交交cdcd于于h h；作作 a ab be ef f,交交c cd d 于于g g(h(h) )， 过过C C任作一任作一条长为条长为c dc d的的线线段段，并由，并由C C点起截取点起截取c c g g 和和g g d d ，得线段分点；得线段分点； 将将线线段末端与段末端与d d点连线，过点连线，过线线段分段分点点作作此此

11、连线的平行线得连线的平行线得g g点点; ;c c g gg g d d 第17页/共82页 解法一解法一 过过D D点在面上作点在面上作ABAB的平行线的平行线 DEDE（DE VDE V面）面）, , 与与ACAC交于交于F,F,由此由此 求出求出A A点，连点，连ad,ad,并作并作ab de.ab de. 解法二解法二 延长延长 和和 ，交于，交于 ， 延长延长cdcd得得e e，作水平线，作水平线eb,eb,即求出即求出 a a和和b b点。点。 c d c d a b a b e ee ee ee ef fe ef fd da ac cb bd dc c平行平行d dc cd dc

12、 cb ba ab ba ab ba a 例例33 已知平面已知平面ABCDABCD的的ABAB边平行于边平行于V V面，补全面，补全ABCDABCD的的HH投影。投影。第18页/共82页 O2l ll lX2113344LPB AAB为所求为所求解题分析解题分析1 1：1.1.包含包含 作平面作平面P 平行平行L；2.2.求求与平面与平面P 的交点的交点A ；3.3.过过A 作直线平行作直线平行L ，该直线在平面，该直线在平面P 内必与内必与相交如相交如B，AB 即为所求。即为所求。第19页/共82页 O2LLX2113344LPQB AAB为为所所求求1.1.包含包含作平面作平面P 平行平

13、行L；2.2.包含包含作平面作平面Q平行平行L；3.3.平面平面P、Q 的交线平行的交线平行L必与必与、相交如相交如AB。解题分析解题分析2 2：第20页/共82页LO2LLX2113344解题分析解题分析3 3：1.1.两次换面两次换面将将( (或或) )变为变为投影面垂投影面垂直线直线；AB2.2.过直线的积聚投影作直线过直线的积聚投影作直线L 的投影的投影l l，则，则该直线必与该直线必与、 都相交。都相交。l l第21页/共82页O2LLX21133441.1.含含作直线作直线L，2.2.求直线求直线与平面与平面的交的交点点A ；55构成平面构成平面L ；3.3.过点过点A 作直线作直

14、线L，交，交于点于点B ；aabbQVab、ab为所求直线的两面投影。为所求直线的两面投影。作图：作图：解题分析解题分析1 1：其它方法解题略其它方法解题略第22页/共82页D D 2. 2. 连连d de e。d de e与与b bc c交于交于f f，在在dede边上作出对应点边上作出对应点f f，连，连bfbf并并延长与延长与c c的垂直投影线相交得的垂直投影线相交得c c点。点。例例5 已知已知AB BCAB BC，补全，补全HH投投影影。e ee ef ff fd dd dc cO OX Xb ba aa ac cb b 1. 1. 过点过点B B作水平线作水平线BDBD ABAB，

15、作正平线，作正平线BEBE ABAB，则平，则平面面BDE ABBDE ABA AB BC C空间解决空间解决E EF F第23页/共82页n nn n例例6 过过MM点作一直线点作一直线MNMN垂垂直于直于 ABCABC，并求其垂足。，并求其垂足。e ee ea ac ca ab bc cb bO OX Xk kd dd dm mm m 1 1 在在 ABCABC内任作水平线内任作水平线CECE和正平线和正平线ADAD，并过，并过m m及及m m点分别作点分别作mn cemn ce，m mn n a ad d，则直线则直线MN ABCMN ABC。 2 2 求求MNMN与与 ABCABC的交

16、点的交点K K，并判断其投影的可见性。，并判断其投影的可见性。k k第24页/共82页b c f h a e abcefh1(2)空间及投影分析空间及投影分析 平面平面EFH是一水平面，它的是一水平面，它的正面投影有积聚性。正面投影有积聚性。a b 与与e f 的交点的交点m 、 b c 与与f h 的交点的交点n 即为两个共有点的正面投影，即为两个共有点的正面投影，故故m n 即即MN的正面投影的正面投影。 求交线求交线 判别可见性判别可见性点点1在在FH上，点上，点2在在BC上，上，点点1在上，点在上，点2在下，故在下，故fh可可见，见，n2不可见。不可见。作作 图图mn 2 nm 1 第

17、25页/共82页例例7 求两平面的交线，并判断可见性。求两平面的交线，并判断可见性。第26页/共82页可通过正面投影可通过正面投影直观地进行判别。直观地进行判别。abcdefc f db e a m (n )空间及投影分析空间及投影分析 平面平面ABC与与DEF都都为为正垂面正垂面，它们的正面投，它们的正面投影都积聚成直线。影都积聚成直线。交线必交线必为一条正垂线为一条正垂线，只要求得只要求得交线上的一个点便可作出交线上的一个点便可作出交线的投影。交线的投影。 求交线求交线 判别可见性判别可见性作作 图图 从正面投影上可看出，从正面投影上可看出，在交线左侧，平面在交线左侧，平面ABC在上，其水

18、平投影可见。在上，其水平投影可见。nm如何判别？如何判别？例：求两平面的交线例：求两平面的交线MN并判别可见性。并判别可见性。第27页/共82页 当两直线均垂直于新投影面当两直线均垂直于新投影面时，两直线在新投影面上的积聚投影即反映时，两直线在新投影面上的积聚投影即反映两直线的距离。两直线的距离。新投影面新投影面C CD DA AB B(b)(b)a ac c空间分析空间分析(d)(d)平行平行a a1 1a ab bc cd da ab bc cd db b1 1c c1 1d d1 1a a2(2(b b2)2)c c2(2(d d2)2)距离距离 例例88 求两平行线求两平行线ABAB、

19、CDCD的距离。的距离。两直线的距离两直线的距离第28页/共82页交叉两管（交叉两管（ABAB和和CDCD）和连接管）和连接管A AB BD DN NMMC Ca ac ca ab bb bc cd dd dX XHHV VV V1 1HHX X1 1c c1 1d d1 1a a1 1b b1 1X X2 2HH2 2V V1 1m mn nn nm mn n1 1m m1 1b b2 2a a2 2c c2 2(d(d2 2) )平行平行平行平行m m2 2(n(n2 2) ) 空间分析空间分析A AB BC CD DMMN N新投影面新投影面a ab bm mc(n)(d)c(n)(d)

20、距离实长距离实长例例9 求两交叉直线的公垂线实长及垂足的投影。求两交叉直线的公垂线实长及垂足的投影。第29页/共82页e ee ec c1 1( e( e1 1 ) )b b1 1a a1 1X X2 2HH1 1V V2 2a ab bc cc cb bHHV VX Xa a例例12 求平面求平面ABCABC的实形和的实形和 角。角。（新轴应垂直于平面内的正平线）（新轴应垂直于平面内的正平线）二次换面二次换面一般面一般面平行面平行面垂直面垂直面X X1 1HH1 1V Va a2 2c c2 2实形实形b b2 2第30页/共82页棱锥棱锥N NMMm mn nHHV VWWn nm mA

21、Ammnna aa am mn nm mn na ammnnaaa aaa 表面上取点表面上取点: 可通过已知点，在点所在的棱面上任作一辅助可通过已知点，在点所在的棱面上任作一辅助线，求出该辅助线的投影，然后求出点的投影。线，求出该辅助线的投影，然后求出点的投影。表面上取点（作辅助线表面上取点（作辅助线MNMN）第31页/共82页V VWWHH圆锥面上取点圆锥面上取点 圆锥面上取点，可用圆锥面上取点，可用直素线法直素线法和和纬圆纬圆法法求。注意后半圆锥面的求。注意后半圆锥面的V V面投影是不可见的面投影是不可见的，右半圆锥面的，右半圆锥面的W W面投影是不可见的。面投影是不可见的。a a直素线

22、法取点直素线法取点纬圆法取点纬圆法取点(c)(c)aas sb ba ac caa(c )(c )a aa ab bs s第32页/共82页第33页/共82页例例10：已知主、左视图：已知主、左视图,求俯视图。求俯视图。第34页/共82页第35页/共82页例例11 求带切口正五棱柱的求带切口正五棱柱的W投影。投影。a ac cd dA AB BC CF FG GD DE Ef f(g)(g)f fg gf fg gb be ec c(d)(d)(c)(c)(d)(d)b b(e)(e)b be ea aa a第36页/共82页第37页/共82页平行平行平行平行平行平行平行平行例12 已知带切口

23、棱锥的主视图，求其俯视图、左视图.(1)(2)第38页/共82页332 2 例例1313 求带缺口正四棱台的求带缺口正四棱台的HH、WW投影。投影。3 34 46 67 72 25 51 1111 15 54 4224455利用利用面上取面上取点点的方法，的方法，求棱面上的求棱面上的几个点几个点. .棱台棱线上棱台棱线上的四个截断的四个截断点点, ,可以直可以直接求出接求出. .注意画出未注意画出未被截切的棱被截切的棱线和两截切线和两截切平面之间的平面之间的交线交线. .6 63 366777 7IIIVVIIVIVIIII第39页/共82页截平面圆柱截交线圆柱截交线圆圆矩形矩形椭圆椭圆截平面

24、与柱轴垂直截平面与柱轴垂直截平面与柱轴平行截平面与柱轴平行截平面与柱轴斜交截平面与柱轴斜交截平面截平面 位置位置截交线截交线 形状形状投影图与立体图投影图与立体图截平面截平面第40页/共82页第41页/共82页圆锥截交线圆锥截交线 截平面截平面垂直于锥轴垂直于锥轴截平面与所有截平面与所有 素线都相交素线都相交截平面平行截平面平行于一条素线于一条素线截平面平行截平面平行于两条素线于两条素线 截平面截平面通过锥顶通过锥顶三角形三角形双曲线双曲线抛物线抛物线椭圆椭圆圆圆截平面截平面 位置位置形状形状截交线截交线投投 影影 图图 与与 立立 体体 图图第42页/共82页 例例15 15 圆锥被两个正垂

25、面截切的画法圆锥被两个正垂面截切的画法 分析分析：一条截交线：一条截交线是椭圆，另一截交线是椭圆，另一截交线是等腰梯形。是等腰梯形。 求两截平求两截平 面交线面交线 求椭圆求椭圆短轴端点短轴端点ddc chhggaaf fe ebb求前后求前后素线交点素线交点 求椭圆长求椭圆长 短轴端点短轴端点b bg gh hc cd de ef fa aa ae e(f)(f)c c(d)(d)g g(h)(h)b b第43页/共82页圆球的截交线圆球的截交线都是都是圆圆 例例1616平行于水平面的圆平行于水平面的圆平行于侧面的圆平行于侧面的圆平行于侧面的圆平行于侧面的圆R3R3R R2 2R R1 1第

26、44页/共82页第45页/共82页第46页/共82页第47页/共82页两平面体相贯两平面体相贯相贯线是两形体表面的公有线相贯线是两形体表面的公有线相贯线一般是封闭的空间折线相贯线一般是封闭的空间折线看清已知条件看清已知条件求各侧棱对另一求各侧棱对另一形体表面的交点形体表面的交点把位于甲形体同把位于甲形体同一侧面又位于乙一侧面又位于乙形体同一侧面上形体同一侧面上的两点，依次连的两点，依次连线线, ,并判断可见并判断可见性（性（只有位于两只有位于两形体都可见的侧形体都可见的侧面上的交线才可面上的交线才可见）。见）。加粗其余轮廓线。加粗其余轮廓线。竖直正四棱柱竖直正四棱柱横置三棱柱横置三棱柱i i

27、(g)(g)bb(d)(d)h h c c i ig gb bd dh hc c(a(a) ) (e (e) ) ( (f f) ) ( (j j) ) (f) (f) (j)(j)e ea a(i)(i)(g)(g)b bd dj j (f)(f)(e)(e)a a (h)(h)C C例例17 求三棱柱与四棱柱的相贯线。求三棱柱与四棱柱的相贯线。第48页/共82页 4,64,6求同坡屋面的求同坡屋面的HH投影投影1 12 23 34 45 56 67 78 81,21,21,81,87,87,87,67,66,56,54,54,53,43,42,32,33,63,62,82,8例例 已知各屋

28、面的已知各屋面的 角为角为3030，求同坡屋面的求同坡屋面的三个三个投影。投影。 1. 1. 各屋檐顺序编号，从各屋角引分角线，并编上号（双号）。各屋檐顺序编号，从各屋角引分角线，并编上号（双号）。 2. 2. 从某一屋角的斜脊开始，将两相交的斜脊编号消去相同的号，从某一屋角的斜脊开始，将两相交的斜脊编号消去相同的号， 得到新的交线号，根据同坡屋面的特点画出此交线。得到新的交线号，根据同坡屋面的特点画出此交线。 3. 3. 根据投影关系画出根据投影关系画出V V、W W投影。投影。3,73,72,72,7第49页/共82页 求同坡屋面的求同坡屋面的HH投影投影例例 已知各屋面的已知各屋面的 角

29、为角为3030，求同坡屋面的求同坡屋面的三个三个投影。投影。 1. 1. 各屋檐顺序编号，从各屋角引分角线，并编上号各屋檐顺序编号，从各屋角引分角线，并编上号( (双号）。双号）。 2. 2. 从某一屋角的斜脊开始，将两相交的斜脊编号消去相同的号，从某一屋角的斜脊开始，将两相交的斜脊编号消去相同的号， 得到新的交线号，根据同坡屋面的特点画出此交线。得到新的交线号，根据同坡屋面的特点画出此交线。 3. 3. 根据投影关系画出根据投影关系画出V V、W W投影。投影。1 12 23 34 45 56 67 78 82,82,84,64,63,73,71,21,21,81,87,87,87,67,6

30、6,56,54,54,52,32,33,43,43,83,83,63,6第50页/共82页 例例补绘俯视图并补主视图的漏线补绘俯视图并补主视图的漏线想象出形体想象出形体的空间形状的空间形状a aA Ab bB Baabb注意注意A、B两点的求法两点的求法a ab b第51页/共82页相贯线是两形体表面的公有线相贯线是两形体表面的公有线相贯线由多段截交线组成相贯线由多段截交线组成平面体和曲面体相贯平面体和曲面体相贯例例18 求三棱柱与半圆柱求三棱柱与半圆柱 的相贯线。的相贯线。相贯线由两段椭圆相贯线由两段椭圆和一段直线组成。和一段直线组成。相贯线在相贯线在H和和W面面为已知，可用为已知，可用圆圆

31、柱柱面上取点面上取点的方法求的方法求V面投影中相贯线面投影中相贯线上的点。上的点。光滑连结相贯线上光滑连结相贯线上的点，并判断可见的点，并判断可见性。性。c c b b d d a (e )a (e )b (d )b (d )c cb bd dc ca ae e( (a )a )( (e )e )第52页/共82页2211(3)(3)bbaa (c)(c)a ab bc c1 12 23 3外圆柱与外圆柱表面相贯线外圆柱与内圆柱表面相贯线内圆柱与内圆柱表面相贯线1 13 32 2a ac cb b例例19 求主视图的相贯线。求主视图的相贯线。第53页/共82页例：求俯视图例：求俯视图第54页/

32、共82页例例20 求半球和圆柱的相贯线。求半球和圆柱的相贯线。先求相贯线的特殊点。先求相贯线的特殊点。用几个辅助平面用几个辅助平面（正平面）截切（正平面）截切两形体，得到相两形体，得到相贯线上的一般点。贯线上的一般点。光滑连结相贯线光滑连结相贯线的点，并判断可的点，并判断可见性。见性。P2P1P3a(b)abbacccd (e )d (f)e (h)dehff (h )圆柱圆柱半球半球圆柱圆柱可见性可见性分界点分界点可见性可见性分界点分界点第55页/共82页第56页/共82页第57页/共82页第58页/共82页X3Y3X2X1X2Z4Z3Z2Z1Y2Y2Y1Z3 正等测图的画法正等测图的画法画

33、组合体的正等测图：画组合体的正等测图：1 1. . 看懂视图，用形体分析法看懂视图，用形体分析法分解形体为四部分。分解形体为四部分。Z2Z4Y32. 2. 先画底部的四棱柱，并在先画底部的四棱柱，并在顶部画出中心线。顶部画出中心线。3. 3. 在四棱柱顶部中心线处对中在四棱柱顶部中心线处对中画出画出四棱台四棱台。4. 4. 在四棱台顶部画出另一四在四棱台顶部画出另一四棱柱。棱柱。5 5. . 在四棱柱顶部正中画出高在四棱柱顶部正中画出高的四棱柱，并画出交线。的四棱柱，并画出交线。6 6. . 加粗加深可见轮廓线，加粗加深可见轮廓线，完成全图。完成全图。X1Y1Z1X2X2Y2Y2四棱柱四棱柱四

34、棱柱四棱柱四棱台四棱台1 1）叠加法叠加法 第59页/共82页 绘制平面立体正等测的基本方法有坐标法和切割法。 2 2）切割法切割法 切割法实际上是坐标法的另一种形式，它是在用坐标法完成作图的基础上，再将多余的部分切割掉。 例例 求作图示求作图示三视图的正等测。三视图的正等测。（1）在三视图上确定坐标原点和坐标轴 （2）作正等轴测轴 （3）沿X、Y、Z轴方向量取36、20、25并连线画出长方体 （4）再量取尺寸18和8，连线得一三角块。O第60页/共82页 绘制平面立体正等测的基本方法有坐标法和切割法。 2 2）切割法切割法 切割法实际上是坐标法的另一种形式，它是在用坐标法完成作图的基础上，再

35、将多余的部分切割掉。 例例 求作图示求作图示三视图的正等测。三视图的正等测。（5）擦去左上角的三角块即得到一斜面 。（6）在原长方体的基础上，量取尺寸10和16,并画出对应的平行线得一梯形块。 第61页/共82页 绘制平面立体正等测的基本方法有坐标法和切割法。 2 2）切割法切割法 切割法实际上是坐标法的另一种形式，它是在用坐标法完成作图的基础上，再将多余的部分切割掉。 （7）擦去梯形块，将可见轮廓线描深。在三视图与轴测投影转换中，只有平行于轴测轴的方向才可以进行测量。 画平面立体的正等测时，首先要选好原点位置和坐标方向，再依据各端点的坐标确定各端点的轴测投影。第62页/共82页 组合体的看图

36、方法组合体的看图方法 看组合体的步骤：看组合体的步骤： 看视图，明关系。看视图，明关系。 分部分，想形状。分部分，想形状。 综合归纳想整体。综合归纳想整体。组合体由长方体挖去五块而成组合体由长方体挖去五块而成第63页/共82页想象出形体的空间形状想象出形体的空间形状 例例20 补绘补绘W投影。投影。第64页/共82页3 3）分析面与面的交线）分析面与面的交线 当物体的局部结构复杂时，应分析面与面的交线。平面与平面相交，交线为直线；平面与曲面相交，交线为平面曲线；曲面与曲面相交，交线一般为空间曲线。交线的性质不同，其作图方法也不相同。 A圆柱体的上端面为平面，圆柱体的上端面为平面，下端有一正垂面

37、下端有一正垂面P P，正垂，正垂面与圆柱体面与圆柱体A A、B B的交线的交线均为椭圆；均为椭圆； 正垂面正垂面P正垂面正垂面P图示的组合体，主视图上有图示的组合体，主视图上有两个粗实线线框，对应俯视两个粗实线线框，对应俯视图为两个圆，所以该组合体图为两个圆，所以该组合体的外形是：的外形是：A为半个小圆柱为半个小圆柱体，体，B为大圆柱体。为大圆柱体。 abbaAB正垂面与圆正垂面与圆柱体柱体A A的交线的交线正垂面与圆正垂面与圆柱体柱体B B的交线的交线二、读图的基本方法二、读图的基本方法 第65页/共82页b ba aaabb例例21 补全补全H投影，并分析线段投影，并分析线段AB是哪两个表面的交线。是哪两个表面的交线。R RQ QB BA AAB是表面是表面R和表面和表面Q的交线的交线b ba aR R平面是侧垂面，平面是侧垂面，其其V V、HH投影是四边形投影是四边形r rr rr rq qqqq qQ Q平面是正垂面，平面是正垂面，其其HH、WW投影是六边形投影是六边形第66页/共82页第67页/共82页 例例2222 已知形体的两视图，求左视图。已知形体的两视图，求左视图。想象出形体想象出形体的空间形状的空间形状第68页/共82页635412第69页/共82页632145第70页/共82页1432第71页/共82