微波技术与天线第1章(3)

1、 长线理论长线理论(传输线理论传输线理论)又称一维分布参数电路理论，是微又称一维分布参数电路理论，是微波电路设计和计算的理论基础。波电路设计和计算的理论基础。 本章从本章从“路路” 的观点出发，研究微波传输线的基本传输特的观点出发，研究微波传输线的基本传输特性，讨论用性，讨论用 SMITH 圆图进行阻抗计算和阻抗匹配的方法。圆图进行阻抗计算和阻抗匹配的方法。长线（传输线）长线（传输线） 用来引导电磁波的装置。用来引导电磁波的装置。导行波：导行波：由传输系统引导，向一定方向传播的电磁波。由传输系统引导，向一定方向传播的电磁波。微波传输线与低频传输线的不同点：微波传输线与低频传输线的不同点： 1.

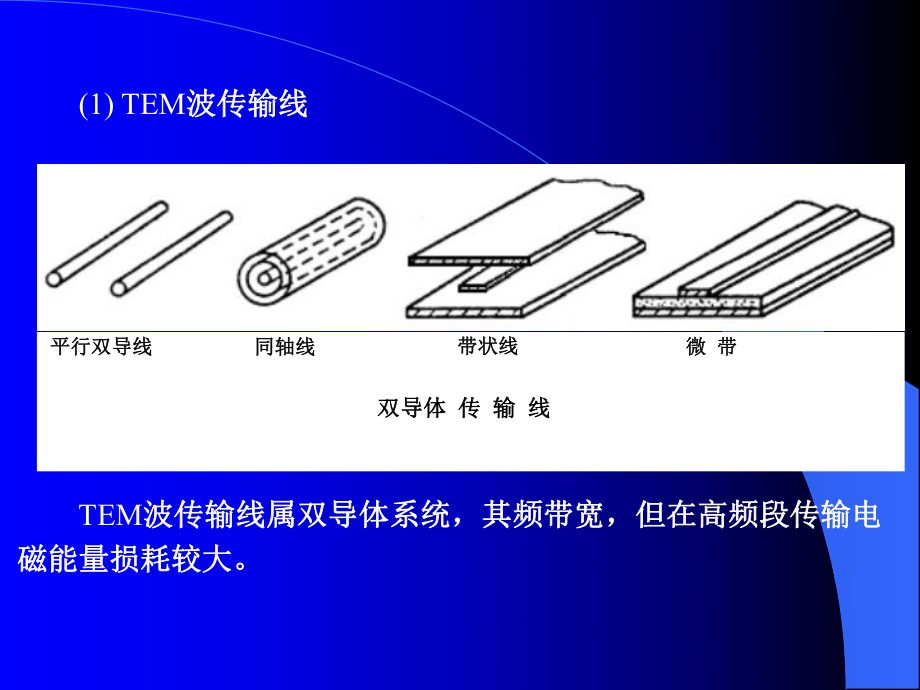
2、 微波传输线种类繁多微波传输线种类繁多, , 按其所传输的导行波型可分按其所传输的导行波型可分为三大类：为三大类：(1) TEM波传输线波传输线 双导体双导体 传传 输输 线线平行双导线平行双导线同轴线同轴线带状线带状线微微 带带 TEM波传输线属双导体系统，其频带宽，但在高频段传输电波传输线属双导体系统，其频带宽，但在高频段传输电磁能量损耗较大。磁能量损耗较大。(2) 金属波导传输线金属波导传输线, 其传输模式为其传输模式为TE、TM波。波。矩形波导矩形波导 圆形波导圆形波导 脊脊 形形 波波 导导椭圆波导椭圆波导 金属波金属波 导导 传传 输输 线线 金属波导传输线属单导体传输系统，又称色

3、散波传输线。金属波导传输线属单导体传输系统，又称色散波传输线。具有损耗小、功率容量大、体积大、频带窄等特点。具有损耗小、功率容量大、体积大、频带窄等特点。(3) 介质（表面波）传输线介质（表面波）传输线介质波导介质波导 镜镜 像像 线线 单根表面波传输线单根表面波传输线 介质介质 传传 输输 线线 主要用于传输表面波主要用于传输表面波, 电磁能量沿传输线的表面传输。具有电磁能量沿传输线的表面传输。具有结构简单、体积小等优点。结构简单、体积小等优点。 当传输线的横截面方向尺寸比线上传输的信号波长小得多、而轴当传输线的横截面方向尺寸比线上传输的信号波长小得多、而轴向尺寸向尺寸 (即长度即长度) 远

4、比信号波长大时远比信号波长大时, 可将传输线看成一维分布参可将传输线看成一维分布参数电路数电路（长线）（长线）。 2. 微波传输线不仅能传输电磁能量微波传输线不仅能传输电磁能量, 还可用来构成各种微波元件还可用来构成各种微波元件( 如谐振腔、滤波器、阻抗匹配器、定向耦合器等如谐振腔、滤波器、阻抗匹配器、定向耦合器等 ) 。这与低频。这与低频传输线截然不同。传输线截然不同。 本节讨论的是传输本节讨论的是传输TEM波的传输线，可用双导线模型进行分析。波的传输线，可用双导线模型进行分析。平行双导线平行双导线同同 轴轴 线线一. 长线与短线的概念长线与短线的概念相对长度相对长度l/ 称为传输线的称为传

5、输线的电长度电长度。 通常，当通常，当 ： l/ 0.05 , 即线长度与工作波长可比拟或更长即线长度与工作波长可比拟或更长的称为的称为长线长线； 当当 ： l / 0.05 , 即线长度与工作波长相比可即线长度与工作波长相比可忽略不计的为忽略不计的为短线短线。 例如：例如： 传输传输3GHz ( =10cm)的同轴线的同轴线, 长长 l = 0.5m, 输送市电的电力传输线输送市电的电力传输线 ( f =50Hz, = 6000 km )， 长长 l 达达几千米，几千米，为为 短线短线。为为 长线长线。 显然，微波传输线属于显然，微波传输线属于“长线长线”的范畴，故本节称的范畴，故本节称为为

6、 “长线理论长线理论” ，即微波传输线基本理论。，即微波传输线基本理论。长线和短线的区别还在于：长线和短线的区别还在于：长线为分布参数电路长线为分布参数电路, , 短线为集总参数电路短线为集总参数电路。 低频电路中低频电路中, 电路元件参数电路元件参数(R、L、C)基本上都集中在相应的基本上都集中在相应的元件元件 (电阻、电感器、电容器电阻、电感器、电容器)中中, 称为集总参数。电路中还存在称为集总参数。电路中还存在着元件间连线的电阻、电感和导线间的电容等，称为分布参数。着元件间连线的电阻、电感和导线间的电容等，称为分布参数。低频电路中低频电路中, 分布参数的量值与集总参数的量值相比微乎其微分

7、布参数的量值与集总参数的量值相比微乎其微, 可忽略不计可忽略不计, 为集总参数电路为集总参数电路。低频传输线为短线低频传输线为短线, 在电路中只在电路中只起连接线作用。起连接线作用。导体周围高频磁场导体周围高频磁场串联分布电感；串联分布电感；两导体间高频电场两导体间高频电场并联分布电容；并联分布电容；传输线上处处存在分布电阻、分布电感，线间处处存在分传输线上处处存在分布电阻、分布电感，线间处处存在分布电容和分布电导。布电容和分布电导。微波信号通过传输线时会产生以下分布参数：微波信号通过传输线时会产生以下分布参数：例：设双导线的分布电感例：设双导线的分布电感L0=0.999nH/mm， 分布电容

8、分布电容C0=0.0111pF/mm ; 工作在工作在 f = 50Hz时引入的时引入的串联电抗、串联电抗、并联导纳：并联导纳： XLf =50Hz=L=2f L0=31410-3 /mm Bcf=50Hz=C=2f C0 =3.4910-12 S /mm当频率升到当频率升到 f = 5000MHz时：时： XLf=5000MHz=L=2fL0 =31.4 /mm Bcf=5000MHz=2fC0 =3.4910-4 S /mm后者是前者的后者是前者的一亿一亿倍倍，其分布参数效应不容，其分布参数效应不容忽视。忽视。当双导线工作在微波波段时，分布参数的影响不容忽视。当双导线工作在微波波段时，分布

9、参数的影响不容忽视。 微波传输线为长线微波传输线为长线, 其电路参数其电路参数 ( ) 及电路物理量及电路物理量 (u、i )，都是沿线分布的，都是沿线分布的(是是 z，t 的函数的函数)，称之为分布参数电路，称之为分布参数电路，必须用传输线理论来研究。必须用传输线理论来研究。 传输线上处处存在分布电阻、分布电感、线间处处存在分布传输线上处处存在分布电阻、分布电感、线间处处存在分布电容和分布电导。根据传输线上分布参数均匀与否，可将传输线电容和分布电导。根据传输线上分布参数均匀与否，可将传输线分为均匀传输线和非均匀传输线。分为均匀传输线和非均匀传输线。 1. 均匀传输线均匀传输线(均匀长线均匀长

10、线)： 分布参数沿线均匀分布，与位置分布参数沿线均匀分布，与位置无关。无关。本节只限于研究均匀传输线。本节只限于研究均匀传输线。1111,R L C G 分布电阻分布电阻 R1 (/m)：单位长度传输线段的总电阻值。与导线：单位长度传输线段的总电阻值。与导线的材料及截面尺寸有关，理想导体的的材料及截面尺寸有关，理想导体的R1 =0。 分布电导分布电导G1(S/m) ：单位长度传输线段的并联电导值。与导：单位长度传输线段的并联电导值。与导线周围介质材料的损耗角有关线周围介质材料的损耗角有关 ，理想介质的，理想介质的G1 =0。 分布电感分布电感 L1 (H/m) ：单位长度传输线段的自感。与导线

11、截面：单位长度传输线段的自感。与导线截面尺寸、线间距及介质的磁导率有关。尺寸、线间距及介质的磁导率有关。 分布电容分布电容C1 (F/m) ：单位长度传输线段间的电容。与导线截：单位长度传输线段间的电容。与导线截面尺寸、线间距及介质的介电常数有关。面尺寸、线间距及介质的介电常数有关。2. 均匀传输线均匀传输线的分布参数分布参数： 对于均匀无耗传输线，对于均匀无耗传输线，R1= 0 ， G1 = 0； 3. 均匀传输线的等效电路均匀传输线的等效电路 对于均匀传输线对于均匀传输线, 由于分布参数均匀分布，故可任取一小段由于分布参数均匀分布，故可任取一小段线元线元 z 0的极限的极限1111( ,

12、)( , )( , )( , )( , )( , )u z ti z tR i z tLzti z tu z tG u z tCzt 得一般传输线方程得一般传输线方程 (电报方程电报方程 )： 时谐传输线方程时谐传输线方程 对于角频率为对于角频率为 的信号的信号, 电压、电流的瞬时值电压、电流的瞬时值u、i与复数与复数U、I的关系为的关系为式中式中( )( )00( )( ) e( )( ) euijzjzU zUzI zIz代入式代入式1-1得时谐传输线方程得时谐传输线方程11d( )( )d ( )( )dU zZ I zdzI zYU zz (12)式中式中111ZRjL 单位长度传输线

13、的串联阻抗，单位长度传输线的串联阻抗，111YGjC 单位长度传输线的并联导钠。单位长度传输线的并联导钠。00( , )( )cos( )Re ( )e( , )( )cos( )Re ( )ej tuj tiu z tUztzU zi z tIztzI z1111( , )( , )( , )( , )( , )( , )u z ti z tR i z tLzti z tu z tG u z tCzt二. 均匀传输线方程的通解均匀传输线方程的通解11d( )( )d(1 2)d ( )( )dU zZ I zzI zYU zz 21122112d( )( )0dd( )( )0dU zZ Y

14、 U zzI zYZ I zz1 1111121 11111()()()()Z YRjLGjCjZ YRjLGjC令令212212d( )d ( )0ddd( )d( )0ddU zI zZzzI zU zYzz 时谐场的传输线方程时谐场的传输线方程式式(1-2) 暂时撇开时间因子暂时撇开时间因子 e j t，而只研而只研究沿线电压、电流的复数振幅与传输线位置之间的关系，是一维空究沿线电压、电流的复数振幅与传输线位置之间的关系，是一维空间的问题。间的问题。将式将式(1-2)对对 z 再一次求导、整理求导、整理: 这是一个二阶齐次常微分方程这是一个二阶齐次常微分方程。、 分别为传输线的传分别为传

15、输线的传播常数、衰减常数和相移常数。播常数、衰减常数和相移常数。222222d( )( )0d(1 3)d( )( )0dU zU zzI zI zz1212( )ee( )eezzzzU zAAI zBB(1) 电压、电流的通解表达式电压、电流的通解表达式均匀传输线的均匀传输线的 与与 z 无关，式无关，式(1-3)的通解为的通解为12111( )( )()zzdU zI zAeA eZdzZ 12120( )(1 4)1( )()zzzzU zAeA eI zAeA eZ即即11110111,ZZRjLZYGjC式式中中Z0 称为传输线的特性阻抗称为传输线的特性阻抗。11d( )( )d(

16、1 2)d ( )( )dU zZ I zzI zYU zz 12120( )1( )()zjzzjzzjzzjzU zAeeA e eI zAeeA e eZ式中含式中含e-j z 的项表示沿的项表示沿z方向方向(由信号源向负载方向由信号源向负载方向)传播的行波，传播的行波，为入射波；为入射波；含含ej z 的项表示沿的项表示沿- -z方向方向(由负载向信号源方向由负载向信号源方向)传播的传播的行波，为反射波。行波，为反射波。( )( )irU zUzj 传输线的传播常数、衰减常数和相移常数。代入传输线的传播常数、衰减常数和相移常数。代入1414( )( )irI zIz图图1-5 长线上的

17、入射波与反射波长线上的入射波与反射波ui(ii)ur(ir)zz入射波入射波反射波反射波l上式是用相量形式表达，根据复振幅与瞬时值的关系，将通解表达成瞬时值lu(z,t)=ReU(z)ejwt=ui (z,t)+ur (z,t)li(z,t)=ReI(z)ejwt=ii (z,t)+ir (z,t) (1-5)l传输线上任何一处的电压传输线上任何一处的电压(或电流或电流)等于等于该处电压该处电压(或电流或电流)的入、反射波的叠加的入、反射波的叠加 三、 均匀传输线方程的定解均匀传输线方程的定解 通解式通解式1-4中的常数中的常数 A1、A2 必须用边界条件即端接条件确定。必须用边界条件即端接条

18、件确定。包括终端条件和始端条件。其中终端条件解是最常用的。包括终端条件和始端条件。其中终端条件解是最常用的。22( )( )zlUlUIlI 以上条件代入式以上条件代入式1-4解得：22022012,22rlrlUI ZUI ZAeAe把终端位置代回式把终端位置代回式1-4：()()220220()()22022000( )22( )22r l zr l zr l zr l zUI ZUI ZU zeeUI ZUI ZI zeeZZ为简化计算，坐标原点坐标原点 z 0 选在终端，即选在终端，即令令zlz图图 已知已知 、 ，求，求 、2U2I( )U z( )I z2U2ILZ0Z0z2202

19、2022022000()22(17)()22rzrzrzrzUI ZUI ZUzeeaUI ZUI ZI zeeZZ式式(-a)写成双曲函数形式220220( )chsh(1 7 )sh( )chU zUzI ZzczI zUIzZ2sh2chzzzzeezeez，xxxxsinhsh,coshch 传输线方程始端条件解自学传输线方程始端条件解自学，注意坐标系与注意坐标系与 终端条件不一样终端条件不一样。 终端入射电压波22022iUIZU22022rUI ZU终端反射电压波222200()()()(17)()()()rzrzirirrzrzirirUzUeUeUzUzbUUIzeeIzIzZ

20、Z1. 传播常数传播常数 四、传输线的特性参数四、传输线的特性参数 均匀无耗长线的分布参数均匀无耗长线的分布参数 R1=0，G1=0，L1、C1均匀分布均匀分布, 与位置与位置 z 无关。（无关。（当信号源频率很高，或长线损耗很小而满足当信号源频率很高，或长线损耗很小而满足条件条件 R1 L1 和和 G1 C1 ，可近似作为无耗长线分析。，可近似作为无耗长线分析。） 表示波经过单位长度传输线后波的振幅和相位的变化。表示波经过单位长度传输线后波的振幅和相位的变化。 为衰减常数为衰减常数, ,波行传播单位长度后幅值的变化，波行传播单位长度后幅值的变化， 单位：单位：B B111111()()Z Y

21、RjLGjCj 为相移常数为相移常数, ,波行传播单位长度后相位的变化，波行传播单位长度后相位的变化，单位：单位：rad2. 相速度和相波长相速度和相波长2121pzzvtt (1-10a) (1) 相速相速vp 相速相速vp 即波的等相位点即波的等相位点移动的速度。移动的速度。 t z =K (常数常数)2211tztz)b42(chsh)(shch)(202022zIZzUzIzZIzUzU)b42(chsh)(shch)(202022zIZzUzIzZIzUzUz2zz1P2P1t1t2u, io图图1-7 不同时刻入射波的瞬时分布不同时刻入射波的瞬时分布 1111()()RjLGjC1

22、1jL C j 即即均匀无耗传输线均匀无耗传输线的传播常数的传播常数 为纯虚数。其为纯虚数。其衰减常数衰减常数 =0，11(1 9b)L C相移常数相移常数 无耗无耗将均匀双导线和同轴线的将均匀双导线和同轴线的L1、C1代入得代入得pv1pv (1 10c)rc (2) 相波长相波长 p相波长相波长 p ：同一瞬间相位相差：同一瞬间相位相差2的两点间的距离。的两点间的距离。111(1 10b)LC0(1 10 )ppprvv Tef均匀无耗双导线均匀无耗双导线当介质为空气时，当介质为空气时，1,rppvc，。)b42(chsh)(shch)(202022zIZzUzIzZIzUzUz2zz1P

23、2P1t1t2u, io图图1-7 不同时刻入射波的瞬时分布不同时刻入射波的瞬时分布 pz31113()()2tztz312pzz11pL Cv自由空间工作波长 上式表明，均匀无耗长线的特性阻抗上式表明，均匀无耗长线的特性阻抗Z0仅取决于长线的截面形状仅取决于长线的截面形状、尺寸和介质尺寸和介质，而与频率无关。因此，而与频率无关。因此，Z0 是表征长线固有特性的一个是表征长线固有特性的一个重要参量。重要参量。11011( )( )iiU zRjLZGjCI z（无耗线无耗线）11LC0121202lnln( )2120ln(1 8 )rDDZddDdd (1) 平行双导线的特性阻抗计算公式平行

24、双导线的特性阻抗计算公式（空气介质）入射波电压比入射波电流微波低损耗线类似 100-1000欧姆200,300,400,600(2) 同轴线的特性阻抗计算公式同轴线的特性阻抗计算公式060ln(1 8 )rbZea 1.1.3 1.1.3 输入阻抗与反射系数输入阻抗与反射系数 图图 传输线的输入阻抗传输线的输入阻抗2U2ILZ)(zZinl0zz0ZinZ1.1. 输入阻抗的定义输入阻抗的定义 长线终端接负载阻抗长线终端接负载阻抗ZL 时，距终端为时，距终端为 z 处向负载方向看去的电压与电流之比处向负载方向看去的电压与电流之比: :( )( )( )inU zZzI z 40-150欧姆 5

25、0,75特性阻抗倒数为特性导纳，用Y0表示长线始端输入阻抗(线长l)由式由式(1-7c)000tan()()(112b)()tanLinLZjZzUzZzZI zZjZz同除以I2chz000t( )( )(1 12a)( )tLinLZjZ h zU zZ zZI zZjZ h z无耗传输线，=0,=j，又得000tan( )(112c)tanLinLZjZlZlZZjZl 输入导纳输入导纳000tan1( )(1 12d)( )tanLininLYjYzYzYZzYjYz001YZ1LLYZ特性导纳特性导纳负载导纳负载导纳导纳用于并联电路。导纳用于并联电路。 ()2ininZznZz 20

26、21()4ininZnZzZz利用此特性可以进行阻抗变换，容性阻抗经过变换可以成为感性。利用此特性可以进行阻抗变换，容性阻抗经过变换可以成为感性。000tan( )tanLinLZjZzZzZZjZz长线电压和电流不能直接测量，阻抗也不能直接测量 Zin(z)的性质的性质(1) Zin(z)随位置随位置 z 而变而变，且与负载阻抗且与负载阻抗 ZL有关有关；(2) 均匀无耗长线的输入阻抗呈周期性变化均匀无耗长线的输入阻抗呈周期性变化，具有/4变换性变换性和和/2重复性：重复性：a. 定义定义电压反射系数电压反射系数( )( )( )riUz zU z电流反射系数电流反射系数( )( )( )r

27、IiIzzI z由式由式(1-7b)得得2222022220222( )( )( )(1 13 )jzjzrijzrIiUI ZU zeeUUI ZUze zbU 从传输功率的观点来看，入射波和反射波的相对幅值是很重要的从传输功率的观点来看，入射波和反射波的相对幅值是很重要的指标。反射波的幅度越小指标。反射波的幅度越小, 传输到负载的功率就越大。可用反射系传输到负载的功率就越大。可用反射系数数 (z)来衡量线上波反射情况。即反射电压波与入射电压波之比来衡量线上波反射情况。即反射电压波与入射电压波之比b. 用反射系数用反射系数 (z) 表示沿线电压、电流分布表示沿线电压、电流分布200( )(1

28、 13 )jzLLZZ zeCZZ 电压反射系数与电流反射系数等模而相位相差电压反射系数与电流反射系数等模而相位相差 ，通常采用通常采用便于测量的电压反射系数作为反射系数便于测量的电压反射系数作为反射系数 (z)。由由U2=I2ZL0( )( )1( )(1 13f)( )( )1( )iiU zU z zU zI z zZ c. (z)与终端反射系数与终端反射系数 的关系的关系把把 =0 代入式代入式 (1-13c) 得终端反射系数得终端反射系数 为为00(1 13 )LLLZZdZZ (z)与与L的关系为的关系为 2( )zL z e对于无耗传输线，有(2)2( )(1 13 )Ljzjz

29、LL z e eg 2 z 为为 (z) 的相位角的相位角对于无源负载01L 2 z ( z )=10o 由式由式(-1g)可见，可见，均匀、无耗传输线任意位均匀、无耗传输线任意位置置 z 处的反射系数一般情处的反射系数一般情况下为一复数，其幅值等况下为一复数，其幅值等于终端反射系数的模，仅于终端反射系数的模，仅由负载决定，与距离无关。由负载决定，与距离无关。相位比终端反射系数的相相位比终端反射系数的相位滞后位滞后2z 。 (z)与与 的关系的关系如图如图1-8所示。所示。图图 1-8 (z)与与的关系示意图的关系示意图滞后角为：24/4zzz若z=/2,电长度1 / 2z滞后角为2每过/2，反射系数的相位改变2 反射系数具有/2重复性若从始端考虑原端反射，则由负载反射系数可得源反射系数00(113)gggZZhZZ反射系数有明确物理意义，便于测量，广泛应用于微波测量技术中由于有反射波，传输线上电压和电流是入射波和反射波的合成。称由于有反射波，传输线上电压和电流是入射波和反射波的合成。称之为之为 行驻波分布。由前式行驻波分布。由前式1-13f(2)2(2)200( )( )1( )1( )( )1( )1LLjzj zii