


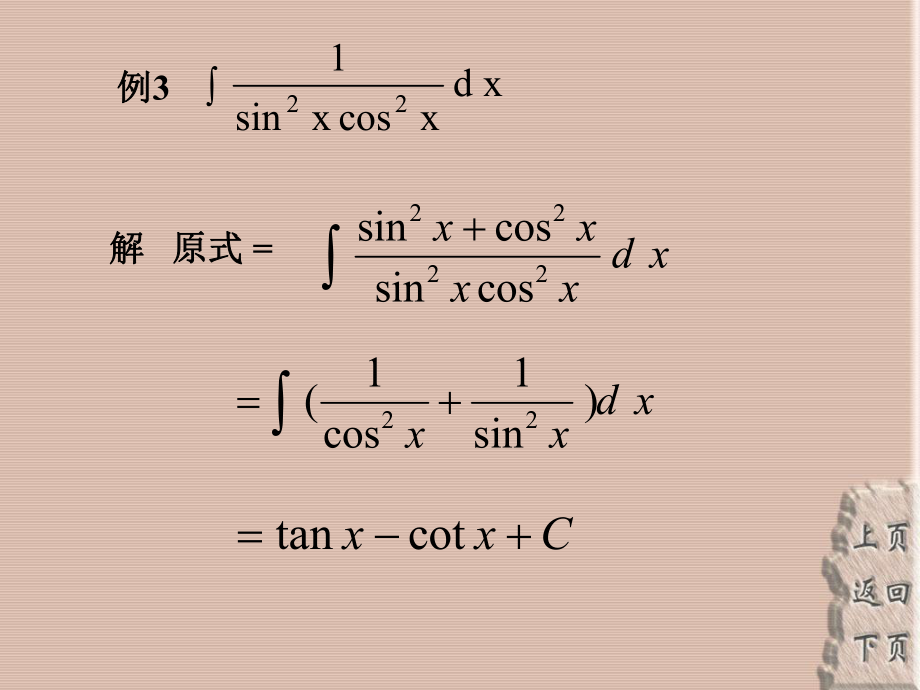

版权说明:本文档由用户提供并上传,收益归属内容提供方,若内容存在侵权,请进行举报或认领
文档简介
1、课题:课题:4.3 换元积分法(一)目的:目的:复习积分的基本公式、性质,掌握积分的第一类换元积分法,并能应用公式、性质熟练地求不定积分重点:重点:第一类换元积分法求不定积分难点:难点:第一类换元积分法求不定积分 复习原函数、不定积分的定义、基本公式、性质复习原函数、不定积分的定义、基本公式、性质 例例1 xd) 1x(x2解解 原式原式 = xdxxx)2(212325Cxxx232527325472例例2 3 x+1e x dx解解 原式原式 = 3(3 e) x dxceexx3ln31xdxcosxsin122例例3 解解 原式原式 = xdxxxx2222cossincossinxd
2、xx)sin1cos1(22Cxxcottanxdxsinx2cos2例例4解解 原式原式 = xdxx22sinsin21xdx)2sin1(2Cxx2cot4.3 换元积分法一、换元积分法一、换元积分法1、第一换元积分法、第一换元积分法.sincosCxxdx?2sin2cosCxxdx第一类换元公式第一类换元公式(凑微分法凑微分法) dxxg)(=.)()( dxxxf设设)(uf具有原函数,具有原函数,)(xu 可可导导,则有换元公式则有换元公式定理定理1 1 dxxxf)()( )()(xuduuf (1)公式的关键在于公式的关键在于如何应用公式(如何应用公式(1)来求不定积分?)来
3、求不定积分?使用此使用此如果如果)(xu (可导)(可导)),()(ufuF 则则.)()( CuFduuf ,)()()()()(xuduufdxxxfdxxg 这样,函数这样,函数 g(x) 的积分即转化为函数的积分即转化为函数 f(u) 的积的积分,如果能求得分,如果能求得 f(u) 的原函数,那么也就得到的原函数,那么也就得到了了 g(x) 的原函数的原函数.分析分析),()(ufuF 则则.)()( CuFduuf相同相同例例1 求求.2cos xdx解解 被积函数中,被积函数中,cos2x 是一个复合函数,是一个复合函数, 把把 2x看作看作u,便有,便有)2(2cos2cosxx
4、dxdxCx2sin2121找找.cosudu例例2 求求xd3xsec2解解 原式原式 = 33sec2xdx3Cx3tan3例例3 求求解解 原式原式 = 31Cx3132xd1x31) 13() 13(21xdx找找duu2sec找找duu21小结:小结:1. 被积函数为单个函数时,找类似的公式,凑被积函数为单个函数时,找类似的公式,凑微分,再积分微分,再积分 例例4 求求xdex73解解 原式原式 = 71Cex7371)73(73xdex找找dueu例例5 求求 22xadx).0( a解解222)(11axdxaxadx.arcsinCax 2)(1axaxd找找21 udu例例6
5、 求求.231dxx 解解找找.|23|ln21Cx duu1dxx231)23(231xdx21练习:求下列不定积分练习:求下列不定积分 5.5.cos(2x-5)dx xd)4x5(131.xdx6112.xd21x53.xdx49124.例例7 求求.2dxxex解解)(222xdedxxexx21Cex221例例8 求求.12dxxx 解解)1 (11222xdxdxxx.)1 (31232Cx21小结:小结:2. 被积函数为几个函数相乘、除时,找函数间的被积函数为几个函数相乘、除时,找函数间的导数关系,凑微分,再积分(保留复杂函数,简导数关系,凑微分,再积分(保留复杂函数,简单函数与
6、单函数与dx凑微分)凑微分) 例例9 9 求求.)ln21( xxdx解解dxxx )ln21(1)(lnln211xdx )ln21(ln21121xdx .)ln21ln(21Cx 例例1010 求求.cossin2xdxx解解)(sinsin2xxd.sin313Cx.cossin2xdxxxd)xtan1 (xcos12例例1111 求求解解xd)xtan1 (xcos12)tan1 (tan11xdx.)tan1ln(Cx 练习:求下列不定积分练习:求下列不定积分 xd1eexx1.xd3xx1x224.xdxxln412.xd)5x(x32323.例例12 求求 xd)2x(x1解解xdxxxx)2()2(21原式xdxx)211(21.)2ln(ln21Cxx小结:第一类换元积分法小结:第一类换元积分法 1. 被积函数为单个函数时,找类似的公式,凑被积函数为单个函数时,找类似的公式,凑微分,再积分微分,再积分 2. 被积函数为几个函数相乘、除时,找函数间的被积函数为几个函数相乘、除时,找函数间的导数关
温馨提示
- 1. 本站所有资源如无特殊说明,都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
- 2. 本站的文档不包含任何第三方提供的附件图纸等,如果需要附件,请联系上传者。文件的所有权益归上传用户所有。
- 3. 本站RAR压缩包中若带图纸,网页内容里面会有图纸预览,若没有图纸预览就没有图纸。
- 4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
- 5. 人人文库网仅提供信息存储空间,仅对用户上传内容的表现方式做保护处理,对用户上传分享的文档内容本身不做任何修改或编辑,并不能对任何下载内容负责。
- 6. 下载文件中如有侵权或不适当内容,请与我们联系,我们立即纠正。
- 7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。
最新文档
- 二零二五宾馆经营权质押合同范例
- 独家代理房产销售协议二零二五年
- 融资系列!融资担保基本认知二零二五年
- 二零二五养殖雇佣合同
- 电影监制合同范例
- 二零二五版理发店劳动的合同
- 信用卡咨询服务协议
- 车间员工管理制度培训
- 转转公司内部管理制度
- 车间安全色标管理制度
- 西工大附中2025届高考英语一模试卷含解析
- 《支付宝相关功能》课件
- 颈椎损伤术后的康复护理
- 2015-2024年十年高考物理真题分类汇编专题05 万有引力与航天(解析版)
- 视觉导航关键技术
- 新能源汽车充电桩项目可行性研究报告模板及范文
- 如何应对学习压力
- 6S组织架构及内容
- 《学前儿童卫生保健》 课件 7.1 托幼园所的生活制度(课件)
- 《人工智能技术基础》课件 第3章 卷积神经网络
- 自考《13180操作系统》考前强化练习试题库及答案

评论
0/150
提交评论