角平分线的性质定理及其逆定理

1、角平分线的性质定理及其逆定理 一、 基础概念学习目标：掌握角平分线的性质定理及其逆定理的证明和简单应用，掌握尺规作图做角平分线，规范证明步骤。（1）角平分线的性质定理证明：角平分线的性质定理：角平分线上的点到这个角的两边的距离相等。证明角平分线的性质定理时，将用到三角形全等的判定公理的推论：推论：两角及其中一角的对边对应相等的两个三角形全等。（AAS）推导过程：已知：OC平分MON，P是OC上任意一点，PAOM，PBON，垂足分别为点A、点B求证：PAPB证明：PAOM，PBONPAOPBO90°OC平分MON12在PAO和PBO中，PAOPBOPAPB几何表达：（角的平分线上的点到

2、角的两边的距离相等）如图所示，OP平分MON（12），PAOM，PBON，PAPB（2）角平分线性质定理的逆定理：到一个角的两边距离相等的点，在这个角的平分线上。推导过程已知：点P是MON内一点，PAOM于A，PBON于B，且PAPB求证：点P在MON的平分线上证明：连结OP在RtPAO和RtPBO中，RtPAORtPBO（HL）12OP平分MON即点P在MON的平分线上几何表达：（到角的两边的距离相等的点在角的平分线上）如图所示，PAOM，PBON，PAPB12（OP平分MON）（3） 角平分线性质及判定的应用为推导线段相等、角相等提供依据和思路；实际生活中的应用例：一个工厂，在公路西侧，到

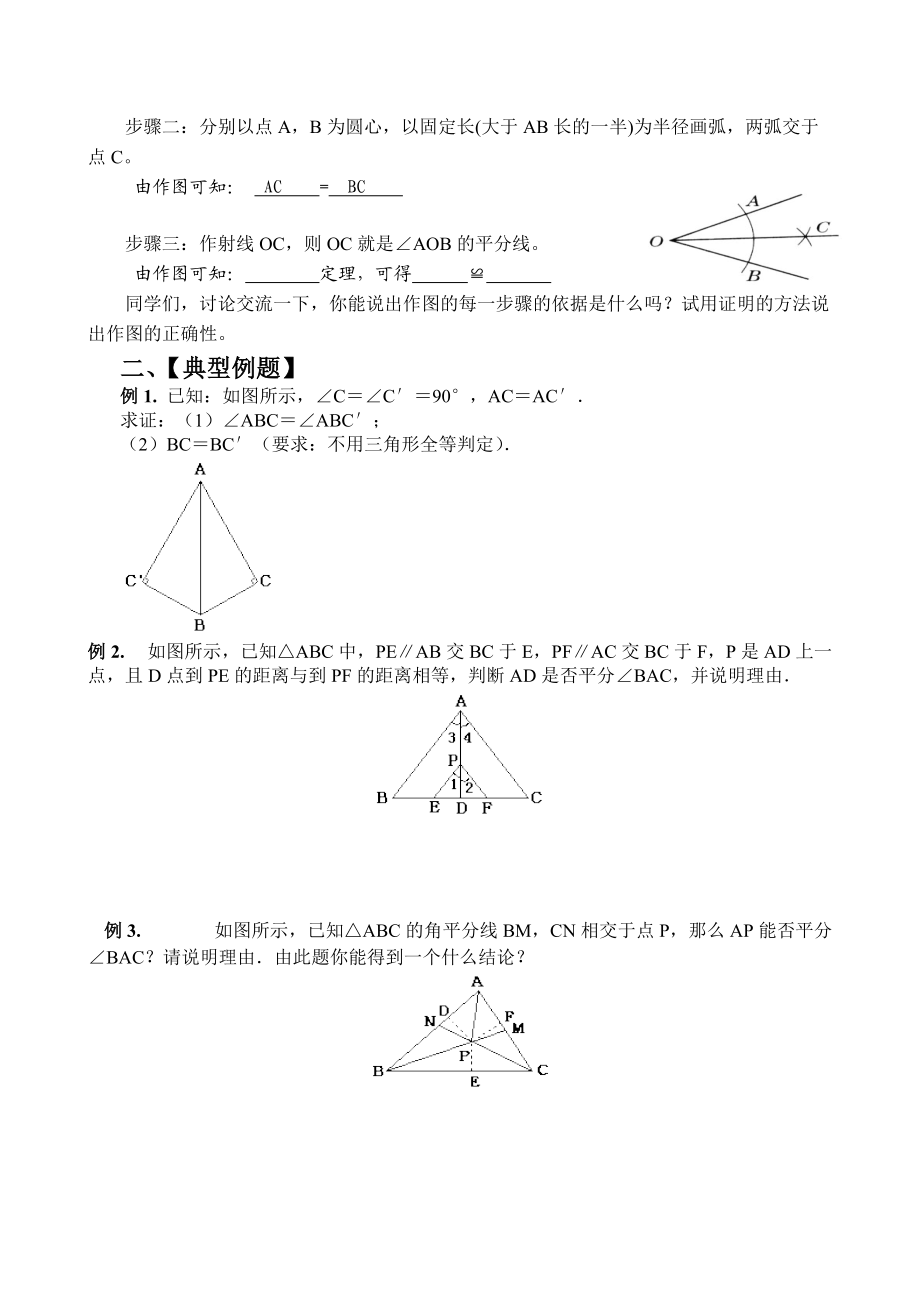
3、公路的距离与到河岸的距离相等，并且到河上公路桥头的距离为300米在下图中标出工厂的位置，并说明理由（4）角平分线的尺规作图活动三：观察与思考： 尺规作角的平分线观察下面用尺规作角的平分线的步骤(如图)，思考这种作法的依据。步骤一：以点O为圆心，以适当长为半径画弧，弧与角的两边分别交于A，B两点。 由作图可知： OA = OB 步骤二：分别以点A，B为圆心，以固定长(大于AB长的一半)为半径画弧，两弧交于点C。 由作图可知： AC = BC 步骤三：作射线OC，则OC就是AOB的平分线。由作图可知： 定理，可得 同学们，讨论交流一下，你能说出作图的每一步骤的依据是什么吗？试用证明的方法说出作图的

4、正确性。二、【典型例题】例1. 已知：如图所示，CC90°，ACAC求证：（1）ABCABC；（2）BCBC（要求：不用三角形全等判定）例2.  如图所示，已知ABC中，PEAB交BC于E，PFAC交BC于F，P是AD上一点，且D点到PE的距离与到PF的距离相等，判断AD是否平分BAC，并说明理由例3.  如图所示，已知ABC的角平分线BM，CN相交于点P，那么AP能否平分BAC？请说明理由由此题你能得到一个什么结论？例4. 如图所示的是互相垂直的一条公路与铁路，学校位于公路与铁路所夹角的平分线上的P点处，距公路400m，现分别以公路、铁路所在直线为x轴、y轴建立

5、平面直角坐标系（1）学校距铁路的距离是多少？（2）请写出学校所在位置的坐标例5. 如图所示，在ABC中，C90°，ACBC，DA平分CAB交BC于D，问能否在AB上确定一点E，使BDE的周长等于AB的长？若能，请作出点E，并给出证明；若不能，请说明理由练习一一、 填空题：1.如图1-31，ABC中，AD是BC的垂直平分线，BE平分ABC交AD于E, EFAB , 则AB = ，BF = ；2.已知：如图1-32，在RtABC中，C = 90°, AC = BC, BD平分ABC交AC于D, DEAB于E，若BC = 5, 则DEC的周长为 .二、选择题：1.如图1-33，A

6、BC中，B = 42°, ADBC于D，E是BD上一点，EFAB于F，若ED = EF, 则AEC的度数为（ ）；A. 60° B. 62° C. 64° D. 66°2.给出下列命题： 垂直于同一条直线的两直线平行； 角平分线上的点到角两边的距离相等； 三角形的三条角平分线相交于一点； 全等三角形的面积相等；其中原命题和逆命题都是真命题的共有（ ）.A. 1个 B. 2个 C. 3个 D. 4个三、解答题：如图1-34，已知：ABC中，BAC = 90°, ADBC于D，AE平分DAC，EFBC交AC于F，连接BF. 求证：BF是A

7、BC的平分线. 【综合练习】已知：如图1-35，ABC中，AB = 2AC, AD平分BAC，且AD = BD. 求证：DCAC. 例题答案例1. 已知：如图所示，CC90°，ACAC求证：（1）ABCABC；（2）BCBC（要求：不用三角形全等判定）证明：（1）CC90°（已知），ACBC，ACBC（垂直的定义）又ACAC（已知），点A在CBC的角平分线上（到角的两边距离相等的点在这个角的平分线上）ABCABC（2）CC，ABCABC，180°（CABC）180°（CABC）（三角形内角和定理）即BACBAC，ACBC，ACBC，BCBC（角平分线上的

8、点到这个角两边的距离相等）例2.  如图所示，已知ABC中，PEAB交BC于E，PFAC交BC于F，P是AD上一点，且D点到PE的距离与到PF的距离相等，判断AD是否平分BAC，并说明理由解：AD平分BACD到PE的距离与到PF的距离相等，点D在EPF的平分线上12又PEAB，13同理，2434，AD平分BAC例3.  如图所示，已知ABC的角平分线BM，CN相交于点P，那么AP能否平分BAC？请说明理由由此题你能得到一个什么结论？解：AP平分BAC结论：三角形的三条角平分线相交于一点，并且这一点到三边的距离相等理由：过点P分别作BC，AC，AB的垂线，垂足分别是E、F、D

9、BM是ABC的角平分线且点P在BM上，PDPE（角平分线上的点到角的两边的距离相等）同理PFPE，PDPFAP平分BAC（到角的两边的距离相等的点在这个角的平分线上） 例4. 如图所示的是互相垂直的一条公路与铁路，学校位于公路与铁路所夹角的平分线上的P点处，距公路400m，现分别以公路、铁路所在直线为x轴、y轴建立平面直角坐标系（1）学校距铁路的距离是多少？（2）请写出学校所在位置的坐标解：（1）点P在公路与铁路所夹角的平分线上，点P到公路的距离与它到铁路的距离相等，又点P到公路的距离是400m，点P（学校）到铁路的距离是400m（2）学校所在位置的坐标是（400，400）评析：角平分线的性质的作用是通过角相等再结合垂直证明线段相等 例5. 如图所示，在ABC中，C90°，ACBC，DA平分CAB交BC于D，问能否在AB上确定一点E，使BDE的周长等于AB的长？若能，请作出点E，并给出证明；若不能，请说明理由解：能过点D作DEAB于E，则BDE的周长等于AB的长理由如下：AD平分CAB，DCAC，DEAB，DCDE在RtACD和Rt