



版权说明:本文档由用户提供并上传,收益归属内容提供方,若内容存在侵权,请进行举报或认领
文档简介
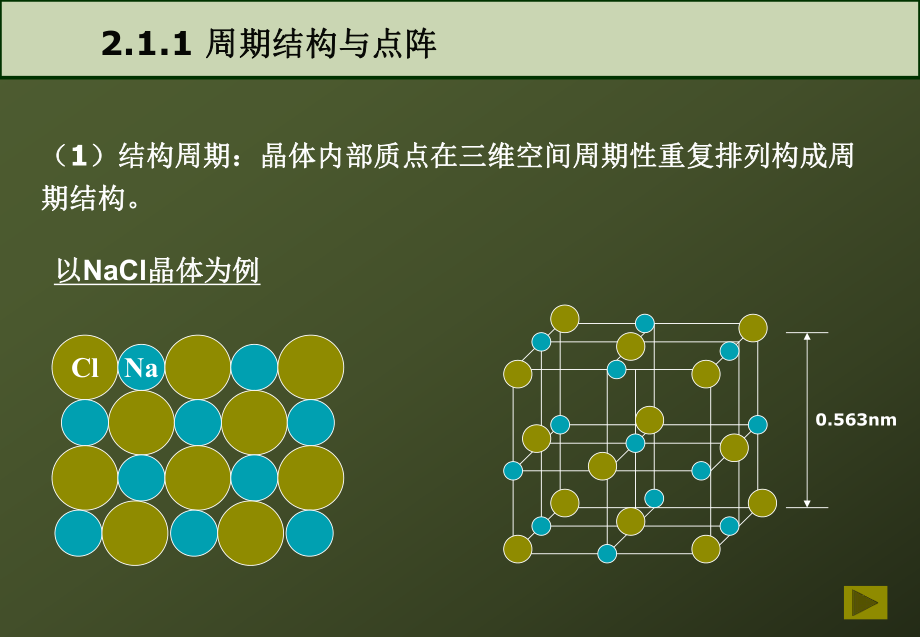
1、第二章 晶体的结构与常见结构类型Chapter 2 Structures and types of crystal晶态结构示意图晶态结构示意图非晶态结构示意图非晶态结构示意图 晶体的定义晶体的定义 由原子、分子或离子等微粒在空间按一定规律、周由原子、分子或离子等微粒在空间按一定规律、周期性重复排列所构成的固体物质。期性重复排列所构成的固体物质。 2.1 晶体的周期结构与点阵3以以NaCl晶体为例晶体为例ClNa0.563nm(1)结构周期:晶体内部质点在三维空间周期性重复排列构成周)结构周期:晶体内部质点在三维空间周期性重复排列构成周期结构。期结构。2.1.1 周期结构与点阵周期结构与点阵 为
2、了研究晶体的周期结构,用数学上的几何点来代表基元的为了研究晶体的周期结构,用数学上的几何点来代表基元的位置,得到位置,得到空间点阵空间点阵。几何点称为空间点阵的几何点称为空间点阵的格点(结点)格点(结点)。 基元:晶体的基本结构单元基元:晶体的基本结构单元 (1) (1) 一个基元对应一个节点一个基元对应一个节点 (2) (2) 基元(结点)周围的环境相同(等效性)基元(结点)周围的环境相同(等效性) (3) (3) 基元内部有结构,可以由一种或数种原子构成基元内部有结构,可以由一种或数种原子构成点阵点阵 + 基元基元 = 晶体结构晶体结构晶体的对称性晶体的对称性点阵的对称性点阵的对称性(2)
3、点阵:)点阵:aa晶体结构晶体结构基元基元点阵点阵),(取整数wvuwcvbuaR用表示所有的点阵点。用表示所有的点阵点。 babac 初基矢量初基矢量点阵参数点阵参数(1)点阵参数:)点阵参数:空间点阵必然可选择空间点阵必然可选择3个不相平行的单位矢量个不相平行的单位矢量a,b,c。点阵参数指三个矢量。点阵参数指三个矢量a,b,c的长度及两两之间的夹角。的长度及两两之间的夹角。(2)元胞:)元胞:不在同一直线上的矢量不在同一直线上的矢量a、b去连接与原点相邻的点阵去连接与原点相邻的点阵点形成的平行四边形,当该平行四边形中只含有一个点阵点时,它点形成的平行四边形,当该平行四边形中只含有一个点阵
4、点时,它就是该平面点阵的最小周期,称为元胞。就是该平面点阵的最小周期,称为元胞。(3)晶胞)晶胞:晶体结构的基本重复单元称为晶胞晶体结构的基本重复单元称为晶胞. NaCl 三维周期排列的三维周期排列的结构及其点阵结构及其点阵(0, 0, 0) (1/2, 1/2, 0) (1/2, 0, 1/2) (0, 1/2, 1/2) abc原子在晶胞中的位置坐标原子在晶胞中的位置坐标Cl- NaCl 三维周期排列的三维周期排列的结构及其点阵结构及其点阵原子在晶胞中的位置原子在晶胞中的位置(1/2,1/20,1/2) ( 0, 1/2, 0) (1/2, 0, 0) (0, 0, 1/2) Na+ 若晶
5、体有完全相同的一种原子组成,则结构基元就只有一个若晶体有完全相同的一种原子组成,则结构基元就只有一个原子,点阵点的位置即是这种原子的位置,由这种原子构成的点阵原子,点阵点的位置即是这种原子的位置,由这种原子构成的点阵即是布拉菲点阵即是布拉菲点阵。布拉菲点阵的特点:布拉菲点阵的特点:每个结点周围的情况都是一样的。每个结点周围的情况都是一样的。如果晶体是由如果晶体是由完全相同的一种原子组成完全相同的一种原子组成,则这种原子所围成的网,则这种原子所围成的网格也就是布拉菲点阵或布拉菲格子,和结点组成的网格完全相同。格也就是布拉菲点阵或布拉菲格子,和结点组成的网格完全相同。(3)布拉菲点阵)布拉菲点阵复
6、式格子的特点复式格子的特点 复式格子是由复式格子是由若干相同若干相同的的布拉菲格子布拉菲格子相互位移套构而成。相互位移套构而成。 (4)复式点阵(格子)复式点阵(格子) 若晶体的基元中包括两种或两种以上的原子,则基元中每种若晶体的基元中包括两种或两种以上的原子,则基元中每种原子可分别构成彼此完全相同的点阵,但它们之间存在相对位移原子可分别构成彼此完全相同的点阵,但它们之间存在相对位移,形成复式点阵。,形成复式点阵。基元结结点点复式格子的特点复式格子的特点点阵类型:(点阵类型:(1)直线点阵)直线点阵以直线连接各个阵点形成的点阵称为直线点阵以直线连接各个阵点形成的点阵称为直线点阵. .结构基元结
7、构基元点阵点阵点阵参数:相邻点阵点的距离点阵参数:相邻点阵点的距离实例实例 最简单的情况是等径圆球密置层最简单的情况是等径圆球密置层. . 每个球抽取为一个点每个球抽取为一个点. . 这些这些点即构成平面点阵点即构成平面点阵. .ab(2)二维平面点阵二维平面点阵( a )NaCl实例实例( b )Cu结构结构点阵点阵晶格晶格ab(c)石墨石墨实例实例结构结构点阵点阵晶格晶格(3)三维三维空间点阵空间点阵简单立方晶格 (a) 简单立方晶格在三维空间延伸 (b)(a)Po 实例实例结构结构点阵点阵晶格晶格结构结构点阵点阵晶格晶格( b )CsCl 实例实例结构结构点阵点阵晶格晶格( c ) Na
8、实例实例结构结构点阵点阵晶格晶格( d )Cu实例实例点阵与晶体关系图点阵与晶体关系图晶体(点阵结构)点阵晶胞正当单位并置切分并置切分把结构单元抽象为几何点把结构单元放回到几何点把结构单元抽象为几何点把结构单元放回到几何点空间点阵几何要素空间点阵几何要素(点线面)点线面)1 结点(结点(node):点阵点阵中中的点。的点。 结点间距:结点间距:相邻结点相邻结点间间的距离。的距离。2 行列行列(row) :结点:结点在直线上在直线上的排列。的排列。 特点特点:平行的行列平行的行列间距相等。间距相等。空间点阵几何要素空间点阵几何要素(点线面)点线面) 面网:面网:由结点在平面上分布构成的平面。由结
9、点在平面上分布构成的平面。 特点:特点:任意两个相交行列便可以构成一个面网。任意两个相交行列便可以构成一个面网。面网密度:面网密度:面网上单位面积内的结点数目。面网上单位面积内的结点数目。面网间距:面网间距:两个相邻面网间的垂直距离,平行面网间距相等。两个相邻面网间的垂直距离,平行面网间距相等。3 面网(面网(net)平行六面体平行六面体:结点在三维空间的分布构成空间格子。:结点在三维空间的分布构成空间格子。特点:特点:任意三个相交且不在同一个平面的行列构成一个空间点阵。任意三个相交且不在同一个平面的行列构成一个空间点阵。根据基矢的不同选择可以得到不同的平行六面体。根据基矢的不同选择可以得到不
10、同的平行六面体。4 平行六面体(平行六面体(parallelepiped)计算由基矢构成的平行六面体点阵点数量时计算由基矢构成的平行六面体点阵点数量时必须考虑:必须考虑:(1)在平行六面体顶角上的点阵点时由)在平行六面体顶角上的点阵点时由8个个相邻平行六面体所共有的;相邻平行六面体所共有的;(2)位于平行六面体棱上的点阵点是由)位于平行六面体棱上的点阵点是由4个个相邻平行六面体所共有的;相邻平行六面体所共有的;(3)位于平行六面体面上的点阵点时)位于平行六面体面上的点阵点时2个相个相邻平行六面体所共有的;邻平行六面体所共有的;(4)位于平行六面体内部的点阵点完全属)位于平行六面体内部的点阵点完
11、全属于该平行六面体。于该平行六面体。l 坐标系体的构成;坐标系体的构成; 原点和三个不共面的基矢原点和三个不共面的基矢a、b、和、和c。2.1.2 2.1.2 三维空间点阵中直线点阵与平面点阵的表达三维空间点阵中直线点阵与平面点阵的表达 定义:定义:表示晶面、晶列(棱)等在晶体上方位的简单的数字符号。表示晶面、晶列(棱)等在晶体上方位的简单的数字符号。 结晶符号结晶符号 l 定义:定义:用简单数字符号来表达晶棱或者其他直线(如坐标轴)用简单数字符号来表达晶棱或者其他直线(如坐标轴)在晶体上的方向的结晶学符号。也称在晶体上的方向的结晶学符号。也称Miller指数。指数。l 三轴定向通式为三轴定向
12、通式为uvw,四轴定向通式为四轴定向通式为uvtw,l 晶晶向向符号的确定步骤:符号的确定步骤: 选定坐标系,以晶轴选定坐标系,以晶轴x x、y y、z z为坐标轴,轴单位分别是为坐标轴,轴单位分别是a a、b b和和c c; 通过原点作一直线,使其平行于待标定晶向通过原点作一直线,使其平行于待标定晶向ABAB; 在直线上任取一点在直线上任取一点P P,求出求出P P点在坐标轴上的坐标点在坐标轴上的坐标x xa a、y yb b、z zc c; x xa a/a:y/a:yb b/b:z/b:zc c/c/c= =u:v:wu:v:w应为整数比,去掉比号,以方括号括之,应为整数比,去掉比号,以
13、方括号括之,写成写成 uvwuvw 即晶向即晶向ABAB的晶向符号。的晶向符号。(1)直线点阵或晶列的表达)直线点阵或晶列的表达晶向符号晶向符号(晶棱符号晶棱符号)u在立方晶系中,晶向指数与晶面指数相同时,则晶面与晶向垂直。在立方晶系中,晶向指数与晶面指数相同时,则晶面与晶向垂直。u不同晶面与晶向具有不同的原子密度,因而晶体在不同方向上表不同晶面与晶向具有不同的原子密度,因而晶体在不同方向上表现出不同的性质。现出不同的性质。ABCO111晶向垂直于(晶向垂直于(111)面)面OA晶向晶向:120OB晶向晶向:103OC晶向晶向:123xyz 取截距系数的倒数比,并化简。即:取截距系数的倒数比,
14、并化简。即: 1/ 1/p:1/q:1/r=p:1/q:1/r=h:k:lh:k:l (h:k:lh:k:l应为简单整数比)应为简单整数比) 去掉比例符号,以小括号括之,去掉比例符号,以小括号括之, 写成(写成(hklhkl), ,即为待标定晶面的晶面指数。即为待标定晶面的晶面指数。晶面符号晶面符号 表示晶面在空间中方位的符号,又称米勒符号。三轴定向通式为表示晶面在空间中方位的符号,又称米勒符号。三轴定向通式为(hkl),四轴定向通式为四轴定向通式为(hkil)。确定晶面符号的步骤:确定晶面符号的步骤: 选定坐标系;选定坐标系; 求出待标晶面在求出待标晶面在x x、y y、z z轴上的截距轴上
15、的截距papa、qbqb、rcrc, ,则截距系数分则截距系数分别为别为p p、q q和和r r;(2)平面点阵或晶面的表达)平面点阵或晶面的表达yxz2:3:331:21:21晶面符号晶面符号 (332)l 晶面在晶轴上的截距系数愈大其晶面符号中与该轴相应的米氏晶面在晶轴上的截距系数愈大其晶面符号中与该轴相应的米氏指数愈小。当晶面平行于某坐标轴时,其晶面符号中的米氏指指数愈小。当晶面平行于某坐标轴时,其晶面符号中的米氏指数为数为0 0。(010)(001)(001)(010)(100)(100)立方体各晶面的晶面符号立方体各晶面的晶面符号xyz341000(0001)010)1(10)1(0
16、六方柱后面三个晶面的晶面符号六方柱后面三个晶面的晶面符号:100)1(x yzu晶面符号:晶面符号:1:)1(:0:111:)11(:1:11)1110(1100)(0110)(1010)2.2.1 2.2.1 对称性的基本概念对称性的基本概念 对称就是物体相同部分有规律的重复。对称就是物体相同部分有规律的重复。l 对称不仅针对几何形态,还有更深和更广的含义,它包含了自然对称不仅针对几何形态,还有更深和更广的含义,它包含了自然科学、社会科学、文学艺术等各领域的对称性,如战争中的科学、社会科学、文学艺术等各领域的对称性,如战争中的非对称非对称战略战略。2.2 点阵宏观对称性与类型点阵宏观对称性与
17、类型晶体对称的特点晶体对称的特点1 1)由于晶体内部都具有格子构造,通过平移,可使相同质点重)由于晶体内部都具有格子构造,通过平移,可使相同质点重复,因此所有的晶体结构都是对称的。复,因此所有的晶体结构都是对称的。2 2)晶体的对称受格子构造规律的限制,它遵循)晶体的对称受格子构造规律的限制,它遵循“晶体对称定晶体对称定律律” ” 。3 3)晶体的对称不仅体现在外形上,同时也体现在物理性质上。)晶体的对称不仅体现在外形上,同时也体现在物理性质上。 由以上可见由以上可见:格子构造使得所有晶体都是对称的,格子构造格子构造使得所有晶体都是对称的,格子构造也使得并不是所有对称都能在晶体中出现的。为什么
18、?也使得并不是所有对称都能在晶体中出现的。为什么?晶体的宏观对称要素和对称操作晶体的宏观对称要素和对称操作 对称操作:对称操作:使对称图形中相同部分重复的操作。使对称图形中相同部分重复的操作。对称要素:对称要素:在进行对称操作时所应用的辅助几何要素(点、线、面)。在进行对称操作时所应用的辅助几何要素(点、线、面)。 操作类型操作类型对称操作对称操作假想的辅助几何要素假想的辅助几何要素对称要素对称要素 简单简单反伸(倒反)反伸(倒反)点点对称中心对称中心反映反映面面对称面对称面旋转旋转线线对称轴对称轴 复杂复杂旋转旋转+反伸反伸线和线上的定点线和线上的定点旋转反伸轴旋转反伸轴旋转旋转+反映反映线
19、和垂直于线的平面线和垂直于线的平面旋转反映轴旋转反映轴晶体的宏观对称操作与对称要素晶体的宏观对称操作与对称要素1 1、对称中心对称中心i i(inversioninversion):):一个假想的几何点,在通过该一个假想的几何点,在通过该点的任意直线的两端可以找到与其等距离的点。点的任意直线的两端可以找到与其等距离的点。对应的对称操作对应的对称操作:对此点的对此点的反伸(倒反)。反伸(倒反)。C 一个晶体中可以有对称中心,也可以没有对称中心;如果有对一个晶体中可以有对称中心,也可以没有对称中心;如果有对称中心,那么只能有一个,且位于晶体的几何中心。称中心,那么只能有一个,且位于晶体的几何中心。
20、 该切面不是矩形体的对称面该切面不是矩形体的对称面该切面是对称面该切面是对称面2 、对称面、对称面m(mirror plane):):一个假想的平面,它能将晶体一个假想的平面,它能将晶体分成互成镜像反分成互成镜像反 映的两个相同部分映的两个相同部分。 对应的对称操作:对应的对称操作:对此面的反映。对此面的反映。B2B1B4B3B2B1B4B3A2A1A4A3A2A1A4A3A2A1A4A3A2A1A4A33 、旋转对称(、旋转对称(n):):通过晶体中心的一条假想的直线,绕这通过晶体中心的一条假想的直线,绕这 条条直线旋转一定的角度后,能使图形相同的部分重复出现。直线旋转一定的角度后,能使图形
21、相同的部分重复出现。 对应的对称操作:对应的对称操作:绕对称轴的旋转。绕对称轴的旋转。 轴次(轴次(n):):旋转一周旋转一周重复的次数重复的次数基转角(基转角( ):):重复时重复时所旋转的最小角度所旋转的最小角度 n与与 之间的关系:之间的关系:/360n 23464 、旋转反伸对称(、旋转反伸对称( ):):通过晶体中心的一条假想的直线,绕通过晶体中心的一条假想的直线,绕这这 条直线旋转一定的角度后再反伸,能使图形相同的部分重复出条直线旋转一定的角度后再反伸,能使图形相同的部分重复出现。现。 对应的对称操作:对应的对称操作:绕对称轴的旋转加反伸。绕对称轴的旋转加反伸。 n 1= i 2=
22、 m324(3个)个) 立方体立方体 六方柱六方柱(4个)个)(6个)个)6 3= 3i 4 6= 3m值得指出的是,除值得指出的是,除4 外,外,其余各种旋转反伸轴都可其余各种旋转反伸轴都可以用其它简单的对称要素以用其它简单的对称要素或它们的组合来代替,其或它们的组合来代替,其间关系如下:间关系如下: 2.2.2 2.2.2 点阵结构的点对称性与点群点阵结构的点对称性与点群 (1 1)点对称特点:)点对称特点:由于晶体是具有格子构造的固体物质,这种质点格子状的分布特点决定了晶体的对称轴只有n = 1,2,3,4,6这五种,不可能出现n = 5, n 6的情况。为什么?为什么?1 1、直观形象
23、的理解:垂直五次及高于六次的对称轴的平面结构不能直观形象的理解:垂直五次及高于六次的对称轴的平面结构不能构成面网,且不能毫无间隙地铺满整个空间构成面网,且不能毫无间隙地铺满整个空间, 即不能成为晶体结构。即不能成为晶体结构。补充补充 2 2、数学的证明方法为:、数学的证明方法为:t = = mtmtt= 2tsin(= 2tsin( -90-90)+ t = -2tcos )+ t = -2tcos + t + t所以,所以,mtmt = -2tcos = -2tcos + t + t 2cos 2cos = 1- m = 1- m coscos = (1 - m)/2 = (1 - m)/2
24、 -2 -2 1 - m 1 - m 2 2 m = -1,0,1,2,3 m = -1,0,1,2,3相应的相应的 0 0 或或2 2 , /3, /3, /2 /2, 2 2 /3, /3, ,相应的轴次为,相应的轴次为1 1,6 6,4 4,3 3,2 2。(但是,在准晶体中可以有(但是,在准晶体中可以有5 5、8 8、1010、1212次轴)次轴)tttt晶系晶系第一位第一位第二位第二位第三位第三位点群点群(共(共32个)个)可能对称元素可能对称元素方向方向可能对称元素可能对称元素方向方向可能对称元素可能对称元素方向方向三斜三斜1, 1任意任意无无无无1, 1单斜单斜2,m,2/mY无
25、无无无2,m,2/m正交正交2,mX2,mY2,mZ222,mm2,mmm四方四方4, 4,4/mZ无,无, 2,mX无,无, 2,m底对角底对角线线4, 4,4/m,422,4mm, 42m, 4/mmm三方三方3, 3Z无,无, 2,mX无无3, 3, 32,3m, 3m六方六方6, 6, 6/mZ无,无, 2,mX无,无, 2,m底对角底对角线线6, 6, 6/m,622, 6mm, 62m, 6/mmm立方立方2,m,4, 4X3, 3体对体对角线角线无,无, 2,m面对角面对角线线23,m3,432, 43m, m 3m晶体学点群的对称元素方向及国际符号晶体学点群的对称元素方向及国际
26、符号(2)点群:)点群:晶体可能存在的对称类型晶体可能存在的对称类型。 通过宏观对称要素在一点上组合运用而得到。只能有通过宏观对称要素在一点上组合运用而得到。只能有32种种对称类型,称对称类型,称32种点群种点群晶族和晶系晶族和晶系在晶体的对称型中,根据有无高次轴和高次轴多少,把在晶体的对称型中,根据有无高次轴和高次轴多少,把3232个对称个对称型划分出三个晶族;又根据对称特点划分为型划分出三个晶族;又根据对称特点划分为7 7个晶系。个晶系。晶体高级晶族(高次轴多于一个)中级晶族(高次轴只有一个)六方晶系 四方晶系 三方晶系 低级晶族(无高次轴)斜方晶系 单斜晶系 三斜晶系 立方晶系晶体的分类
27、晶体的分类n2晶体学点群的对称元素方向及国际符号晶体学点群的对称元素方向及国际符号晶系晶系第一位第一位第二位第二位第三位第三位点群点群可能对称元可能对称元素素方向方向可能对称元可能对称元素素方向方向可能对称元可能对称元素素方向方向三斜三斜1, 1任意任意无无无无1, 1单斜单斜2,m,2/mY无无无无2,m,2/m正交正交2,mX2,mY2,mZ222,mm2,mmm四方四方4, 4,4/mZ无,无, 2,mX无,无, 2,m底对角底对角线线4, 4,4/m,422,4mm, 42m, 4/mmm三方三方3, 3Z无,无, 2,mX无无3, 3, 32,3m, 3m六方六方6, 6, 6/mZ
28、无,无, 2,mX无,无, 2,m底对角底对角线线6, 6, 6/m,622, 6mm, 62m, 6/mmm立方立方2,m,4, 4X3, 3体对体对角线角线无,无, 2,m面对角面对角线线23,m3,432, 43m, m 3m 7大晶系晶格的关系大晶系晶格的关系a立立方方aaaaa三三方方三三斜斜abc正正交交abcabc单单斜斜aaac六六方方aac四四方方14 种布拉菲点阵种布拉菲点阵简单三斜简单三斜( (P) ) 090,cba简单单斜简单单斜( (P) )底心单斜底心单斜(C)1 1)三斜晶系:)三斜晶系: 2 2)单斜晶系:)单斜晶系: ,cba3 3)三方晶系:)三方晶系:三
29、方三方( (R) )0012090 cba4 4)正交晶系:)正交晶系:090 ,cba简单正交简单正交( (P) )底心正交底心正交( (C) )体心正交体心正交( (I) )面心正交面心正交( (F) )5 5)四方晶系)四方晶系090 cba体心四方体心四方( (I) )简单四方简单四方( (P) )6.6.六角晶系:六角晶系:0012090 cba六角六角( (H) )7 7)立方晶系:)立方晶系:090 cba简立方简立方( (12) )体心立方体心立方( (13) )面心立方面心立方( (14) )2.2.3 晶体结构对称性与物性的关系晶体结构对称性与物性的关系 晶体的物理性质往往
30、与方向有关,这也就意味着晶体结构晶体的物理性质往往与方向有关,这也就意味着晶体结构的对称性对于物理性质有着很大的影响。实际上,早就有的对称性对于物理性质有着很大的影响。实际上,早就有NeumannNeumann原理指出:晶体的任何物理性质必定具有它所属的点原理指出:晶体的任何物理性质必定具有它所属的点群的一切对称性。因此,表征晶体物理性质的参量群的一切对称性。因此,表征晶体物理性质的参量物质常物质常数也必将与晶体的对称性有关。数也必将与晶体的对称性有关。 1)矢量(一阶张量)物质常数:)矢量(一阶张量)物质常数: 矢量具有三个分量,即为一阶张量。例如,铁电晶体之类矢量具有三个分量,即为一阶张量
31、。例如,铁电晶体之类的强电介质中的自发极化矢量就是一种矢量物质常数。晶体中的强电介质中的自发极化矢量就是一种矢量物质常数。晶体中的这种矢量物质常数的存在与否就将要受到晶格对称性的限制。的这种矢量物质常数的存在与否就将要受到晶格对称性的限制。 (2)二阶张量物质常数:)二阶张量物质常数: 由两个矢量物理量所决定的常数是二阶张量,它含有由两个矢量物理量所决定的常数是二阶张量,它含有9个个分量。例如,介电常数、极化率、电导率、磁化率、热导率、扩分量。例如,介电常数、极化率、电导率、磁化率、热导率、扩散系数等,都是二阶张量常数。这种物质常数的分量数目即决定散系数等,都是二阶张量常数。这种物质常数的分量
32、数目即决定于晶体的对称性。于晶体的对称性。以介电常数以介电常数为例:为例: 电位移矢量电位移矢量D与电场强度矢量与电场强度矢量E之间的关系为:之间的关系为: D = E 当通过施行晶体的对称操作之后,这种关系不会改变,从当通过施行晶体的对称操作之后,这种关系不会改变,从而可以证明:在具有四面体对称性和立方对称性的晶体中,介电而可以证明:在具有四面体对称性和立方对称性的晶体中,介电常数等二阶张量物质常数必将是一个对角张量,即有:常数等二阶张量物质常数必将是一个对角张量,即有: D =oENewman原理:原理: 晶体的任一物理性质所拥有的对称要素必须包含晶体所属晶体的任一物理性质所拥有的对称要素
33、必须包含晶体所属点群的对称要素。点群的对称要素。两层含义:两层含义:第一层含义包括以下两点:第一层含义包括以下两点:(1)晶体的物理性质可以而且经常具有比晶体结构所属点群更高)晶体的物理性质可以而且经常具有比晶体结构所属点群更高的对称性。的对称性。(2)晶体物理性质的对称性不能低于晶体结构所属点群的对称性。)晶体物理性质的对称性不能低于晶体结构所属点群的对称性。第二层含义:第二层含义: 晶体某些物理性能在对称要素取向方面的关系,即物性张晶体某些物理性能在对称要素取向方面的关系,即物性张量的对称性等于或高于晶体点群的对称性。量的对称性等于或高于晶体点群的对称性。2.3.12.3.1点阵的微观对称
34、要素点阵的微观对称要素 宏观对称的主要特征:宏观对称的主要特征: -有限图形的对称。有限图形的对称。 -对称要素的组合在空间相交于一点(没有平移操作)。对称要素的组合在空间相交于一点(没有平移操作)。 微观对称的主要特征:微观对称的主要特征: -无限图形的对称。无限图形的对称。 -对称要素的组合呈空间分布(有平移操作)。对称要素的组合呈空间分布(有平移操作)。 晶体内部构造中除其外形上可能出现的对称要素外,还晶体内部构造中除其外形上可能出现的对称要素外,还 出现特有的、与平移有关的微观对称要素:出现特有的、与平移有关的微观对称要素: 平移轴平移轴 滑移面滑移面( (象移面象移面) ) 螺旋轴螺
35、旋轴 2.3 2.3 点阵结构的微观对称性点阵结构的微观对称性- -空间群空间群平移轴平移轴:为一直线方向,图形沿此直线移动一定距离,可为一直线方向,图形沿此直线移动一定距离,可 使相同部分重复。使图形复原的最小平移距离,使相同部分重复。使图形复原的最小平移距离, 称平移轴的移距。称平移轴的移距。 说明说明:- 晶体构造中,任一行列方向都是一个平移轴,行列的结晶体构造中,任一行列方向都是一个平移轴,行列的结 点间距即为平移轴的移距,因此任何一个空间格子均有点间距即为平移轴的移距,因此任何一个空间格子均有 无穷多的平移轴。无穷多的平移轴。滑移面滑移面( (象移面象移面) ):一假想的平面,当图形对此平面反映后,一假想的平面,当图形对此平面反映后,在平行此平面的某一方向上移动一定距离,可使图形的相同部分在平行此平面的某一方向上移动一定距离,
温馨提示
- 1. 本站所有资源如无特殊说明,都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
- 2. 本站的文档不包含任何第三方提供的附件图纸等,如果需要附件,请联系上传者。文件的所有权益归上传用户所有。
- 3. 本站RAR压缩包中若带图纸,网页内容里面会有图纸预览,若没有图纸预览就没有图纸。
- 4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
- 5. 人人文库网仅提供信息存储空间,仅对用户上传内容的表现方式做保护处理,对用户上传分享的文档内容本身不做任何修改或编辑,并不能对任何下载内容负责。
- 6. 下载文件中如有侵权或不适当内容,请与我们联系,我们立即纠正。
- 7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。
最新文档
- 2025年大学《纺织工程-机织工程》考试备考试题及答案解析
- 物理试卷+答案湖北省十堰市八校教联体2025-2026学年高二9月联考(9.25-9.26)
- 灯具厂客服部售后响应工作方案
- 珠宝公司团队建设管控方案
- 《规范仪容仪表不带手机入校》演讲稿
- 家具公司财务预算管理办法
- 规范汉字书写培训
- 我国进城务工人员随迁子女异地高考政策的多维价值剖析与展望
- 我国资产证券化发展:历程、现状、挑战与机遇的深度剖析
- 智能仓储物流信息追溯系统在化妆品分销行业的创新应用可行性报告2025
- 供应室护士长年底工作总结
- 英国汽车工业市场分析现状供需格局投资前景未来规划研究报告
- 血液净化中心护士长2025年度述职报告
- 人格特质课件
- 八上物理光学试卷及答案
- 2026年杨凌职业技术学院单招职业技能测试题库及参考答案详解
- 2025年中国医美童颜针产业发展研究报告
- 眼科医疗风险防范培训
- 2025至2030老年手机行业产业运行态势及投资规划深度研究报告
- 违禁物品X射线图像与识别课件
- 2025年新疆中考道德与法治试卷(含答案)

评论
0/150
提交评论