第4章-建筑力学及结构-第2版资源

1、1第四章第四章 平面一般力系的简化及平衡方程平面一般力系的简化及平衡方程 41 平面平面一般力系的简化一般力系的简化 42 平面一般力系的平衡方程及其应用平面一般力系的平衡方程及其应用 43 物体系的平衡问题物体系的平衡问题 2力系力系 空间力系空间力系 平面力系平面力系 平面一般力系平面一般力系 ：各力的作用线都处于同一平面内，它们既不完全汇交于一点，相互间也不全部平行。 平面汇交力系：平面汇交力系：各力作用线全部汇交于一点。 平面平行力系：平面平行力系：各力作用线全部平行。 空间一般力系空间一般力系 空间汇交力系空间汇交力系 空间力偶系空间力偶系 3 4-1 4-1 平面一般力系的简化平面

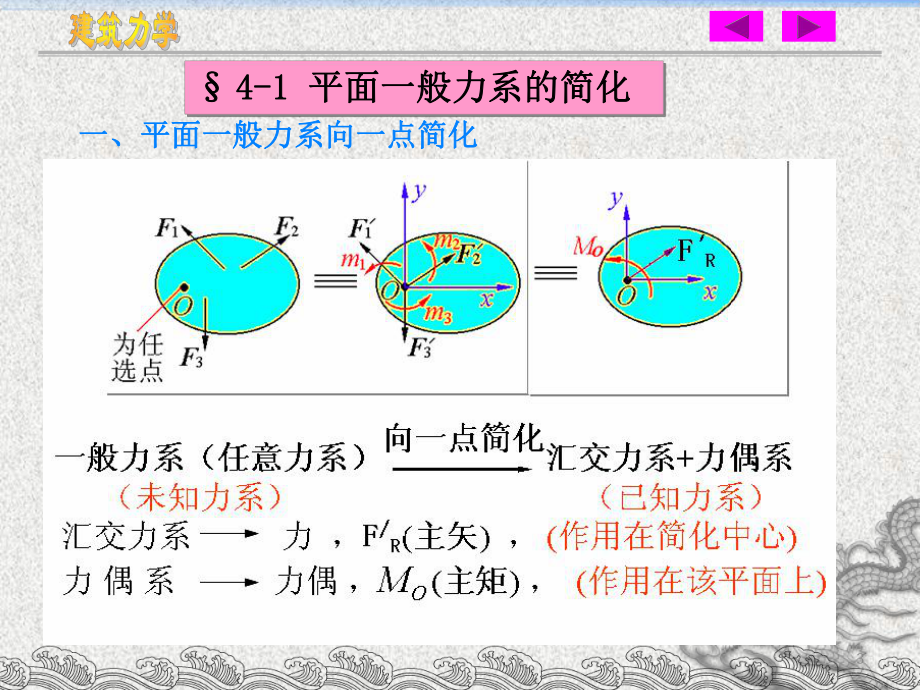
2、一般力系的简化 一、平面一般力系向一点简化一、平面一般力系向一点简化 4 大小大小： 主矢主矢 方向方向： 简化中心简化中心 (与简化中心位置无关) 因主矢等于各力的矢量和RFiRFFFFF321主矢)()()( 21321iOOOOFmFmFmmmmM主矩222/2/)()(yxRyRxRFFFFFxyRxRyFFFF11tgtg（移动效应移动效应）5 大小大小： 主矩主矩MO 方向方向： 方向规定 + 简化中心简化中心： (与简化中心有关) （因主矩等于各力对简化中心取矩的代数和）)(iOOFmM（转动效应转动效应） 力系的主矩一般与简化中心的位置有关。因而，对于主矩，必须指明简化中心的位

3、置，符号M0的下标表示简化中心为O点。 6简化结果： 主矢 ，主矩 MO ，下面分别讨论。RF二、平面一般力系的简化结果讨论二、平面一般力系的简化结果讨论 1 1、平面一般力系简化为一个力偶的情形、平面一般力系简化为一个力偶的情形若 ， ，表明作用于简化中心O的力F F1 1 、F F2 2 、F Fn n相互平衡，因而相互抵消。但是，附加的力偶系并不平衡，可合成为一个合力偶，即为原力系的合力偶，力偶矩等于因为力偶对于平面内任意一点的矩都相同，因此当力系合成为一个力偶时，主矩与简化中心的位置无关。 0RF)(00FmM00M7 （1） ,表明附加力偶系为一平衡力系，亦可撤去，那么一个作用在简化

4、中心O点的力与原力系等效。显然， 就是这个力系的合力，合力的作用线通过简化中心O。合力矢等于力系的主矢，即 （此时 与简化中心有关，换个简化中心，主矩不为零）2 2、平面一般力系简化为一个合力的情形、平面一般力系简化为一个合力的情形0, 0oRMFRFFFFRR（2 2） ,则原力系与作用线过简化中心的一个力和一个同平面的力偶等效，原力系可以继续简化为一原力系可以继续简化为一个合力。个合力。如下图所示0, 00MFR8合力 的作用线应在作用线应在O点哪一侧，须根据力 对O点的矩的转向与 的转向一致原则来确定。 RFRF0M9)(1niiOOFmM)()(主矩ORROMdFFm)()(1niiO

5、ROFmFM 合力矩定理合力矩定理：由于主矩 而合力对O点的矩 合力矩定理 由于简化中心是任意选取的，故此式有普遍意义。 即：平面一般力系的合力对作用面内任一点之矩等于力系平面一般力系的合力对作用面内任一点之矩等于力系 中各力对于同一点之矩的代数和。中各力对于同一点之矩的代数和。R103 3、平面一般力系平衡的情形、平面一般力系平衡的情形若 ， 时，这表明原力系与两个平衡力系等效，即原力系既不能使物体有移动效应，又不能使物体产生转动效应，所以物体平衡，故原力系为平衡力系。0RF00M总结平面一般力系的最后简化结果，当 时，原力系要么平衡，要么是一个力偶；当 时，不论主矩是否为零，原力系合成结果

6、都是一个力。平面一般力系的最后简化结果与简化中心的位置无关，因为最后简化结果为：要么是平衡、要么是一个力偶、要么是一个力，三者必居其一。这三种结果与简化中心的位置都无关 0RF0RF11例例重力坝受力如图所示，设W1=450kN，W2=200kN，FP1=300kN，FP2=70kN，求力系的合力的大小和方向，及合力与基线OA的交点到点O的距离x.12解：解： 以O为坐标原点，建立坐标系Oxy，将力系向O点简化，主矢 在X、Y轴上的投影为：RF)7 .1697 . 2arctanarctan(95.232)7 .16cos70300(cos0021CBABkNkNFFFFPPxRx其中13kN

7、kNFWWFFPyRy670)7 .16sin70200450(sin0221kNFFFRyRxR33.709)670()95.232()()(2222083.709 .232670arctanarctanRxRyFF14顺）(2355)2009 . 34505 . 13003(9 . 35 . 13)(21100mkNmkNWWFFmMP在哪个象限由 与 的正负来判定。因为 为正， 为负，故 在第四象限内，与X轴夹角为70.830。 （如图）FRFRxFRyFRxFRyFRF15 因为 ，所以原力系合成结果是一个合力。合力大小和方向与主矢相同，因为M0为负值，合力对O点的矩也应该为负值，故合

8、力的作用线必在O点的右侧，如图4-4所示。合力的作用线与基线的交点到点O 的距离x，可根据合力矩定理求得。即0, 00MFRmmFMxxFFmFmFmMRyRyRyRxR5 . 3)6702355(0)()()(00000解得16 4-2 4-2 平面一般力系的平衡平面一般力系的平衡方程方程及其应用及其应用平面一般力系平衡的必要和充分条件：力系的主矢和力平面一般力系平衡的必要和充分条件：力系的主矢和力系对于任一点的矩都等于零，即系对于任一点的矩都等于零，即1.平衡方程的基本形式平衡方程的基本形式0, 00MFR由此平衡条件可导出不同形式的平衡方程。)()()(22FmMFFFooyxR0)(0

9、0FmFFoyx17由此可得结论，平面一般力系平衡的解析条件是：所有各力在两个任选的坐标轴上的投影的代数和都等于零；力系中所有各力对任一点的力矩的代数和等于零。 需要指出的是，上述平衡方程是相互独立的，用来求解平面一般力系的平衡问题时，能且最多只能求解三个未知量。为了避免求解联立方程，应使所选的坐标轴尽量垂直于未知力，所选矩心尽量位于两个未知力的交点（可在研究对象之外）上。此外，列平衡方程时，既可先列投影方程，也可先列力矩方程。总之，应尽量使每一方程式中只含一个未知量，以便简化计算。180, 0RAxFxF由022; 0)(aPmaaqaFFmRBA0yF0PqaFFRBRAy例例 已知：P=

10、20kN, m=16kNm, q=20kN/m, a=0.8m 求：A、B的支反力。解：研究AB梁解得：)kN(122028 . 01628 . 02022PamqaFRB)kN(24128 . 02020RBRAyFqaPF19例例如图所示一钢筋混凝土刚架的计算简图，其左侧面受到一水平推力P=5KN的作用。刚架顶上有均布荷载，荷载集度为q=22KN/m，刚架自重不计，尺寸如图所示，试求A、B处的支座反力。 解：研究钢架由0 xF0RBxPFF0yF03qFFRByRA0)(FmB023333qFFRAP解得：kNFRBx5kNFRA28kNFRBy3820QPCBAC整理得2.平衡方程的二矩

11、式平衡方程的二矩式0)(0)(0FmFmFBAx（A与B两点的连线不垂直于x轴） 3.平衡方程的三矩式平衡方程的三矩式0)(0)(0)(FmFmFmCBA（A、B、C三点不共线） 21应用平面一般力系的平衡方程求解平衡问题的解题步骤如下：（1）确定研究对象根据题意分析已知量和未知量，未知量要用已知量来表示，所以研究对象上一定要有已知量，选取适当的研究对象。（2）画受力图 在研究对象上画出它受到的所有主动力和约束反力。约束反力根据约束类型来画。当约束反力的指向未定时，可以先假设其指向。如果计算结果为正，则表示假设指向正确；如果计算结果为负，则表示实际的指向与假设的相反。（3）列平衡方程选取适当的

12、平衡方程形式、投影轴和矩心。尽量避免解联立方程，应用投影方程时，投影轴尽可能选取与较多的未知力的作用线垂直；应用力矩方程时，矩心往往取在两个未知力的交点。计算力矩时，要善于运用合力矩定理，以便使计算简单。（4）求解：解平衡方程，求解未知量。（5）校核22例例如图所示拱形桁架的一端A为铰支座，另一端B为滚轴支座，其支承面与水平面成倾角300。桁架自重G=100KN,风压力的合力Q=20KN,其方向水平向左，试求A、B 支座反力。 230)(FmA060sin204100RBPFFG0)(FmB010420GFFPRAy0 xF060cos0PRBRAxFFF解得：kNFRB4 .62kNFRAy

13、46kNFRAx2 .11解：1、选桁架为研究对象，画出其受力图 2、列平衡方程选A、B两点为矩心，用二矩式 24平面汇交力系、平面平行力系和平面力偶系，皆可看作平面一般力系的特殊力系，它们的平衡方程皆可由平面一般力系的平衡方程导出。 平面汇交力系的平衡方程平面汇交力系的平衡方程00yxFF2）平面汇交力系平衡的必要与充分的几何条件是：力多边形自行封闭力多边形自行封闭1）平面汇交力系平衡的必要与充分的解析条件是：各力在两个坐标轴各力在两个坐标轴上投影的代数和分别等于零上投影的代数和分别等于零 利用几何法求解平面汇交力系的平衡问题时，画出自行封闭的力多边形 ，然后按比例尺从力多边形中直接量出未知

14、力的大小即可。 25例例 求当F力达到多大时，球离开地面？已知P、R、h解解：1）研究块,受力如图，由力三角形：cosFFN)2(1)(cos22hRhRRhRR)2(hRhRFFN解得：262）再研究球，受力如图：作力三角形sinNFPRhRsin又NNFFRhRhRhRFFPN)2(sin)2()(hRhhRFPhRhRhPF)2(时球方能离开地面当hRhRhPF)2(27平面平行力系平面平行力系:各力的作用线在同一平面内且相互平行的力系。2、平面平行力系的平衡方程、平面平行力系的平衡方程平面平行力系平衡方程的一般形式：0)(0FmFoy平面平行力系平衡方程的二矩式：0)(0)(FmFmB

15、A（A、B两点连线不与诸力平行） 各力在x轴上的投影恒等于零，即 所以只有两个独立方程，只能求解两个独立的未知量。 0 xF28例例 塔式起重机如图所示，机架重G=700KN，作用线通过塔架中心。最大起重量FW1=200KN，最大悬臂长为12m，轨道A、B的间距为4m，平衡块重FW2，到机身中心线距离为6m。试问：1、保证起重机在满载和空载都不致翻倒，求平衡块的重量FW2应为多少？2、当平衡块重FW2=180KN时，求满载时轨道A、B给起重机轮子的反力。29解解：1）画起重机受力图，如图这些力组成平面平行力系2、求起重机在满载和空载时都不致翻倒的平衡块重FW2的大小 当满载时，为使起重机不绕B

16、点翻倒，这些力必须满足平衡方程MB（F）=0在临界情况下，FRA=0，限制条件FRA0,才能保证起重机不绕B点翻倒。30 0Bm0)22()212(2)26(12RAWWFFGF限制条件：0RAF解得：kNGFFWW75821012 当空载时，此时FW1=0,为使起重机不绕A点翻倒，则必须满足平衡方程mA（F）=0,在临界情况下，FRB=0，限制条件FRB0,才能保证起重机不绕A点翻倒。0)(FmA0)22(2)26(2RBWFGF限制条件：0RBF解得：kNGFW3502231由于起重机实际工作时不允许处于极限状态，要使起重机不会翻倒，平衡块重量满足关系：kNFkNW350752(3)、当F

17、W2=180kN时，求满载（FW1=200kN）情况下，轨道A、B给起重机轮子的反力FRA、FRB。0)(FmA04)212(2)26(12RBWWFFGF 0yF012RBRAWWFFFGF解得：kNFRB870kNFRA210323 3、平面力偶系的平衡方程、平面力偶系的平衡方程 由于平面力偶系合成的结果为一合力偶，M=m，而力偶在任一轴上投影的代数和均为零。即平面一般力系的平衡方程的基本形式的两个投影方程均变成恒等式，故平面力偶系的平衡方程为： 0m即平面力偶系平衡的充要条件是：力偶系中各力偶矩的代数和为零。独立平衡方程数目是一个，能且只能求解出一个未知数 一个未知力偶或一对未知力（力偶

18、臂已知时）。 33 例例 梁AB的支座和受力情况如图所示。已知m=10kNm，不计梁重，试求两支座反力。 解解：1）选梁AB为研究对象,画分离体受力图 2）列平衡方程，求解未知量 0m045cos40mFRA解得：kNmFFRBRA5 . 345cos40根据力偶与力偶平衡的概念，A支座反力与B支座反力组成一个力偶与m平衡。 34 4-3 4-3 物体系的平衡问题物体系的平衡问题 物体系统（物系物系）：由若干个物体通过约束所组成的系统。物系平衡的特点：物系平衡的特点： 当物体系平衡时，组成该系统的每一个物体都处于平衡状态。 每个单体可列3个平衡方程，整个系统可列3n个方程（设物系中有n个物体）

19、在求解静定的物体系的平衡问题时，可以选每个物体为研究对象，列出全部平衡方程，然后求解；也可以先取整个系统为研究对象，列出平衡方程，求出部分未知量，再从系统中选取某些物体作为研究对象，列出另外的平衡方程，直至求出所有的未知量为止。 35 为了使求解过程尽可能简便，并且避免出现反复。解决物系的平衡问题时，应当首先从有已知力作用的，而未知力数目少于或等于独立平衡方程数的物体开始着手分析。把有已知力作用，未知数少于或等于独立平衡方程数的条件称为可解条件。对于符合可解条件的分离体先行求解，将求得物体系的内力，通过作用与反作用关系，转移到其他物体作为已知力，逐步扩大已知量的数目直至最终求出所有未知量。 有

20、时还可能出现这样的情况，就整个物系而言是静定的，而物系的所有分离体无一符合可解条件。此时必存在有的分离体上虽有四个未知力，但存在三个未知力汇交于同一点或互相平行的情况，取汇交点为矩心或取平行力的垂线为投影轴即可解出部分未知力和其余未知力之间的关系，再以其他分离体为研究对象，逐个把所有未知力求出。把分离体有已知力作用，虽有n3个未知力，但有（n-1）个汇交或平行的条件，称为部分可解条件。对于这类没有符合可解条件的分离体的问题，应先从符合部分可解条件的分离体着手解起。36例例 已知：连续梁上，P=10kN, Q=50kN, CE 铅垂, 不计梁重 求：A ,B和D点的反力（看出未知数多于三个，不能

21、先整 体求出，要拆开） 0Fm由0512PQFRG)kN(50210550RGF解解：研究起重机370610123, 0QPFFmRDRBA 再研究整体 再研究梁CD0cm016RGRDFFkNFRD33. 86500yF0PQFFFRDRBRAykNFkNFRBRAy10033.4838例例 如图所示为钢结构拱架。拱架由两个相同的刚架AC和BC用铰链C连接，拱脚A、B用铰链固结于地基，吊车梁支承在刚架的突出部分D、E上。设两刚架各重为FW=60KN；吊车梁重为G=20KN，其作用线通过点C；荷载重为FP=10KN；风力F=10KN，尺寸如图所示。D、E两点在FW的作用线上，求铰链A和B的约束

22、反力。解：1）先研究吊车梁画受力图0)(FmD0248PREFGF解得：kNFRE5 .122）研究整体画受力图0)(FmA052104612FFFFGFWWPRBy39400yF02WPRByRAyFGFFF 0 xF0RBxRAxFFF解得：kNFRBy5 .77kNFRAy5 .723）研究右半刚架画受力图0)(FmC044106REWRBxRByFFFF解得：kNFRBx5 .17kNFRAx5 . 741习题课习题课3平衡; 0, 0ORMF合力矩定理合力矩定理)()(1iniOROFmFm; 0, 0; 0, 0ORORMFMF或1合力（主矢）; 0, 0ORMF2合力偶（主矩） 一、平面一般力系的合成结果一、平面一般力系的合成结果本章小结：本章小结：42一矩式一矩式 二矩式二矩式 三矩式三矩式二、二、平面一般力系的平衡方程平面一般力系的平衡方程0)(00FmFFoyx0)(0)(0FmFmFBAx0)(0)(0)(FmFmFmCBA轴不xAB不共线、CBA0 xF平面平行力系的平衡方程平面平行力系的平衡方程一矩式一矩式0)(0FmFoy二矩式