信息论与编码(第二版)曹雪虹(最全版本)答案

1、信息论与编码(第二版)曹雪虹答案第二章一i个马尔可夫信源有3个符号ui,U2,U3 ,转移概率为：p ui|ui1/2,p U21 ui1/2,p u3|u10 , p u1|u21/3 , p u2|u20 , p u3|u22/3, p u1 |u31/3 ,p u2| u32/3 ,p u3|u3 0,画出状态图并求出各符号稳态概率。解：状态图如下状态转移矩阵为：1/2 1/ 20p 1/302/31/3 2/30设状态U1,U2, U3稳定后的概率分别为 W1, W2、W3WP WW1 W2111W1-W2 -W3 W1102521323W1得2W1-W33W2计算可得W2912W22

2、5W363W325W1 W2 W31W3p(0|01) p(10|01) 0.5p(0|10)p(00 |10) 0.5p(1|01) p(11|01) 0.5由符号集0, 1组成的二阶马尔可夫链，其转移概率为：p(0|00)二, p(0|11)二, p(1|00)=,p(1|11)= p(0|01) = , p(0|10) =p(1|01) 二 , p(1|10)=。画出状态图，并计算各状态的稳态概率。解：p(0|00) p(00100) 0.8p(0|11)p(10|11) 0.2p(1| 00)p(01| 00) 0.2p(1|11)p(11|11) 0.8p(1|10)p(01|10)

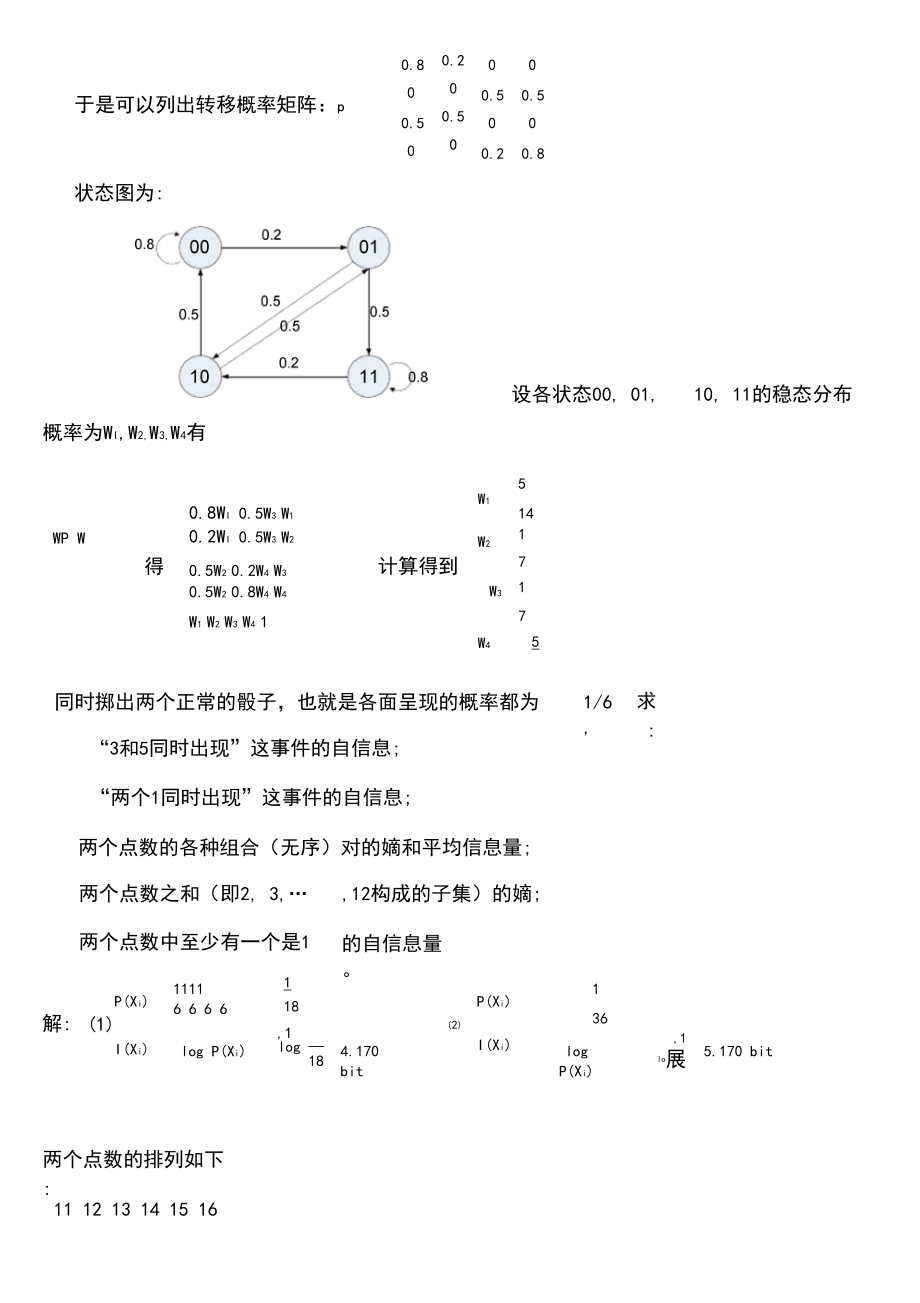
3、0.5于是可以列出转移概率矩阵：p0.800.500.200.5000.500.200.500.8状态图为:设各状态00, 01,10, 11的稳态分布概率为Wl,W2,W3,W4有WP W0.8Wi 0.5W3 W1W15140.2Wi 0.5W3 W2W210.5W2 0.2W4 W3计算得到7175140.5W2 0.8W4 W4W1 W2 W3 W4 1W3W4得同时掷出两个正常的骰子，也就是各面呈现的概率都为1/6,求:“3和5同时出现”这事件的自信息;“两个1同时出现”这事件的自信息;两个点数的各种组合（无序）对的嫡和平均信息量;两个点数之和（即2, 3,12构成的子集）的嫡;两个

4、点数中至少有一个是1的自信息量。解:P(Xi)(1)I(Xi)11116 6 6 6log P(Xi)118,1log 184.170 bitP(Xi)I(Xi)136log P(Xi),1lo展5.170 bit两个点数的排列如下:11 12 13 14 15 1621 22 23 24 25 26313233343536414243444546515253545556616263646566共有21种组合:其中11, 22, 33, 44, 55, 66的概率是二6136其他15个组合的概率是2晨118H(X)布10gB 4.337 bit/symbolP(X)H(X)P(Xi)I(Xi)

5、2-4234 5 61111536 18 12 9 36p(xjog p(x。85362 Log 1 2 Log 工 363618183.274bit /symbol11log P(Xi)113611log 1.710 bit36(2) -Log = Q.D14-LogICiO10 11211118121361 .1一|1。51511log 2 log - 2 log log 1212993636 66+-LolOOO = OjOtSl11p(Xi)log p(Xi)6 log 15i3636(4)参考上面的两个点数的排列，可以得出两个点数求和的概率分布如下:居住某地区的女孩子有25%是大学生

6、，在女大学生中有75%是身高160厘米以上的，而女孩子中身高160厘米以上的占总数的一半。假如我们得知“身高 160厘米以上的某女孩是大学生”的消息，问获得多少信息量解：设随机变量X代表女孩子学历X X1 (是大学生)X2 (不是大学生)P(X)设随机变量Y代表女孩子身高Y yi (身高 >160cm)y2 (身高 <160cm)P(Y)已知：在女大学生中有75%是身高160厘米以上的即：p(y1/x1) 0.75 bit求：身高160厘米以上的某女孩是大学生的信息量即：I (x1/y1)logp(x1/y1)log p(x1)p(y1 /x1)log 0.25 0.75 1.41

7、5 bitP(y1)0.5掷两颗骰子，当其向上的面的小圆点之和是3时，该消息包含的信息量是多少当小圆点之和是7时，该消息所包含的信息量又是多少解：1)因圆点之和为3的概率p(x) p(1,2) p(2,1) 18该消息自信息量 I (x) log p(x) log18 4.170bit2)因圆点之和为7的概率1p(x) p(1,6) p(6,1) p(2,5)p(5,2)p(3,4)p(4,3)6该消息自信息量 I (x) log p(x) log6 2.585bit设有一离散无记忆信源，其概率空间为X ：佼°:w：3P 3/81/41/41/8(1)求每个符号的自信息量(2)信源发

8、出一消息符号序列为202 120 130 213 001 203 210 110 321010 021 032 011 223 210,求该序列的自信息量和平均每个符号携带的信息量解：I(x1) log 2 log 2 8 1.415bit P(x1)3同理可以求得 1(x2) 2bit, I(x3) 2bit,I(x3)3bit因为信源无记忆，所以此消息序列的信息量就等于该序列中各个符号的信息量之和就有：I 141(x1)131(x2)121(x3)61(x4)87.81bit平均每个符号携带的信息量为87回1.95bit/符号 45试问四进制、八进制脉冲所含信息量是二进制脉冲的多少倍解：四

9、进制脉冲可以表示4个不同的消息，例如：0,1,2, 3八进制脉冲可以表示8个不同的消息，例如：0, 1,2, 3, 4, 5, 6, 7二进制脉冲可以表示2个不同的消息，例如：0,1假设每个消息的发出都是等概率的，则：四进制脉冲的 平均信息量H(XJ logn log 4 2 bit/symbol八进制脉冲 的平均信 息量H(X2) log n log 8 3 bit / symbol二进制脉冲的平均信息量 H (X0) logn log 2 1 bit/symbol所以：四进制、八进制脉冲所含信息量分别是二进制脉冲信息量的2倍和3倍。2-9“用三个脉冲用一个脉冲4134(1) I(尸Log(

10、4) 2 I(-)= Log -0.415(2) H= - Log(4) -Log -0.811344312m口IC2-10 /山+ 呵/0918(2) P(黑/黑尸五P(白/黑尸-一 1 T f 14A . 10 T fl4AH(Y/黑尸石LogJ不L阿元j三"幻(3) p(黑/白尸np(白/白尸iH(Y/白尸 /叫了尸不叫5人口网(4)P(黑尸石P(白尸三 H(Y)= m Log(3i) * : Lag！ ( 1 = 0,918有一个可以旋转的圆盘，盘面上被均匀的分成38份，用1,，38的数字标示，其中有两份涂绿色，18份涂红色，18份涂黑色，圆盘停转后，盘面上的指针指向某一数字

11、和颜 色。(1)如果仅对颜色感兴趣，则计算平均不确定度(2)如果仅对颜色和数字感兴趣，则计算平均不确定度(3)如果颜色已知时，则计算条件嫡解：令X表示指针指向某一数字，则 X=1,2,.,38Y表示指针指向某一种颜色，则 Y=l绿色，红色，黑色Y是X的函数，由题意可知p(xiyj) p(xi)，一312381838.一(1) H (Y)p(yj)log - -log 2 -log - 1.24b让/ 付尸j 1p(yj) 3823818(2) H(X,Y) H (X) log 238 5.25bit/符号(3) H(X|Y) H(X,Y) H(Y) H(X) H(Y) 5.25 1.24 4.

12、01bit/ 符号两个实验 X 和Y,X=xiX2X3,Y=yiy2y3,l联合概率 rxyrj 为r 11r12r137/241/240r21r22r231/241/ 41/24r31r32r3301/247/24(1)如果有人告诉你X和Y的实验结果，你得到的平均信息量是多少(2)如果有人告诉你Y的实验结果，你得到的平均信息量是多少(3)在已知Y实验结果的情况下，告诉你 X的实验结果，你得到的平均信息量是多少X17241/240X21/241/41/24X301/24724H (X,Y)p(xi,yj)10g 2Z|og24 247X概率分布H (Y) 3XX1X2X3P8/248248/2

13、4H(X |Y)=符号Yy1y2y3P8/248248/241-log 23 1.58bit/符号H (X,Y) H (Y) 2.3 1.581p(xi, yj)1 , 八 1 ,4 24 log 224 4 log 24=符号Y概率分布是有两个二元随机变量X和Y,它们的联合概率为yxX1=0X2=1y1=01/838y2=1381/8并定义另一随机变量Z = XY （一般乘积），试计算:(1) H(X) H(Y), H(Z), H(XZ), H(YZ) H(XYZ)(2) H(X/Y), H(Y/X), H(X/Z), H(Z/X), H(Y/Z), H(Z/Y), H(X/YZ), H(Y

14、/XZ) H(Z/XY); I(X;Y), I(X;Z), I(Y;Z), I(X;Y/Z), I(Y;Z/X) I(X;Z/Y)。解：13P(Xi)P(X2)P(Xi yi) p(xi y2)8 8p(X2 yi) P(X2y2)H(X)p(Xi) log p(Xi) 1 bit/symbol131p(y1) P(X1 y1) p(X2y1)- -8 82311p(y2)p(xy2)p(X2y2)-882H (Y) p(yj)log p(yj) 1 bit / symbolZ = XY的概率分布如下:ZP(Z)H(Z)Zi0 z2 17188(、7.7 1.1p(Zk)8log8 810g8

15、0.544 bit / symbolp(X1) p(XZ1)p(X1Z2)p(XZ2)0p(X1Z1)p(X1)0.5p(z1)p(X1Z1)p(X24)pH,)p(Z1) p(X1Z1) 78p(Z2)p(X1Z2) p(X2Z2)0.51pQ)p%)-8H (XZ)p(XiZ。10g p(XiZk)i k1i13|3111log loglog 一2288881.406 bit/symbolp(y1)p(y1Z1)p(yZ2) 0p(yZ1) p(y1) p(Z1) p(y1Z1)p(y2。)p(Z1)p(Z2) p(y1Z2)p(y2Z2) p(Z2)p(yZ2)0.5p( 丫2乙)p(y

16、Z1) 7 0.5 8p(y2Z2)18og1 310g 3 1122 88 881.406 bit/symbolH(YZ)p(yjZk)10g p(yjZk)j kp(xyiZ2) 0p(x1y2Z2)0P(X2y1Z2)0p(xyiZi) p(Xi yiZ2)p(xyi)p(xyiZi) p(xyi) 1/8p(xy2z1) p(xi yiZi)p(xZi)11 3p(xy2Zi)p(xizi) p(xiyizi) 2 8 8p(x2yzi) p(x2y/2) pdv)，、，、3p(x2yzi)p(x2 yi) 8P(x2y2。)0p(x2y2。) P(x2y2Z2) p(x2y2) ip

17、(x2y2Z2)p(x2y2) 8H (XYZ)p(xiyjZk)log2 p(xiyjZk)i j ki.8ii bit / symboli. i 3,3 3,3 i, ilog log log log 888888881.811 bit/symbolH(XY)p(xyj)log2 P(xyj)1,13,33,31,1log log loglog oooooooo88888888H(X/Y) H(XY)H(Y/X) H(XY)H(X/Z) H(XZ)H(Z/X) H(XZ)H(Y) 1.811 1 0.811 bit/symbolH(X) 1.811 1 0.811 bit/symbol H

18、(Z) 1.406 0.544 0.862 bit/symbol H(X) 1.406 1 0.406 bit/symbolH(Y/Z)H(YZ) H(Z) 1.406 0.544 0.862 bit/symbolH(Z/Y)H(YZ) H(Y) 1.406 1 0.406 bit/symbol0.405 bit / symbol0.405 bit / symbol 0 bit / symbolH(X/YZ) H (XYZ) H(Y/XZ) H (XYZ) H (Z / XY) H (XYZ)H(YZ) 1.811 1.406H(XZ) 1.811 1.406H(XY) 1.811 1.811

19、I(X;Y) H(X) H (X/Y) 1 0.811 0.189 bit/symbolI(X;Z) H(X) H (X/Z) 1 0.862 0.138 bit/symbolI(Y;Z) H(Y) H(Y/Z) 1 0.862 0.138 bit/symbolI(X;Y/Z)I(Y;Z/X)I(X;Z/Y)H(X/Z)H(Y/X)H (X /Y)H (X /YZ) H(Y/XZ) H(X/YZ)0.862 0.405 0.457 bit/symbol0.862 0.405 0.457 bit/symbol0.811 0.405 0.406 bit/symbol2-14FM)=(21P(ij)

20、=P(i/j尸16 Jp(刈=I +1616173p(yi) =1-3芯1616(2)方法1:729 .联丫户p(yO)西叩)+论1)吸川二木侬+ -0236 = 0311 1616方法2:2-15P(j/i)=Lt+ Log s Q i03111-3 EE 1 - B J-(1 - e)PW-P(blal)= j戌明1Log=Log=L 口 e)J(a1;b2)= Leg黑白传真机的消息元只有黑色和白色两种，即X=黑，白, 一般气象图上，黑色的出现概率P（黑）=,白色出现的概率P（白）=。（1）假设黑白消息视为前后无关，求信源嫡H（X）,并画出该信源的香农线图（2）实际上各个元素之间是有关联

21、的，其转移概率为：P（白|白户，P（黑|白）=,P（白|黑）=,P（黑|黑）=,求这个一阶马尔可夫信源的信源嫡，并画出该信源的香农线图。（3）比较两种信源嫡的大小，并说明原因。解：（1） H（X） 0.3log 210 0.7log 210 0.8813bit/符号 37P（黑|白尸P（M）P（白|白）=P（白）P（黑|黑）=P（黑）P(白|黑)=P(白)（2）根据题意，此一阶马尔可夫链是平稳的（P（白）=不随时间变化，P（M）=不随时间变化）H (X) H(X2|X1)p(xi,yj)10g 21p(x,yj)1 0.9143 0.7log 20.08570.914310.8 0.3log2

22、 0.80.71og 210.085710.2 0.3log2 =符号每帧电视图像可以认为是由3 105个像素组成的，所有像素均是独立变化，且每像素又取128个不同的亮度电平，并设亮度电平是等概出现，问每帧图像含有多少信息量若有一个广播员，在约10000个汉字中选出1000个汉字来口述此电视图像，试问广播员描述此图像所广播的信息量是多少（假设汉字字汇是等概率分布，并彼此无依赖）若要恰当的描述此图像，广播员在口述中至少需要多少汉字解：1）H (X) 10g2 n log2 128 7 bit / symbol H(XN) NH(X) 3 105 7 2.1 106 bit/symbolH(X)

23、log2 n log210000 13.288 bit/symbol 2)H(XN) NH(X) 1000 13.288 13288 bit/symbol3)NH(XN)H(X)2.1 10613.288158037给定语音信号样值X的概率密度为p2 ex，求Hc（X）,并证明它小于同样方差的正态变量的连续嫡Hc(X)px(x)log px(x)dx1Px(x)log 2dxPx(x)(x)log edxlog1 logelog 1 log e1 e20 12lxl(x)dxx)dxlog 1 e x( x)dx o 2log1 2log2xedxlog 210g 2logelogeE(X)

24、0,D(X)1H (X,) -log2(1x)e,2e log 2-221e 2 log4 e22 . e 2、e e log logH(X)连续随机变量X和Y的联合概率密度为：p(x,y)12 r0，求 H(X), H(Y), H(XYZ)其他和 I(X;Y)。(提不：0210g 2 sin xdx y log2 2 )解:p(x)22r xp(xy)dyI xr2 x21Tdy rHc(X)rr p(x) log p(x)dxp(x)logp(x)log2 r22 r-2y dxr2dxrr p(x)log . r22 .x dx其中:log2 r22 rlog log 2 rr22,r

25、p( x) log V rx dxlog r 11210g 2 ep(x) log r2 x2dx r12 log 2 ebit / symbolr2Alog r2x2dxr r4 r 22节 .r x r2 0log . r2 x2dx0r sin log r sin2d(r cos )_2 sinlog r sin d4 2sin20log r sin4 2sin20log rd222sinolog sin d4 Tlog r 2cos224 210cos2 .-log sin d22log r 02 cos2 d 一 02 log sin d2 万 八，.02 cos 2 log sin

26、 d- logr 02dlog1 logr 02dsin22一(log2 2)2222 cos 20log sin dlog02 cos2log sin dlog210g 2 e其中:cos2log sin d02 log sin dsin 2sin 2 log sin2 sin 2 d log sin122 2 sin cos 0cossin10g 2 ed2 .-log 2 e522 cos02 log 2 e110g 2 e2d0110g2e02 cos2 d1 .2 log 2 e1 .2 log 2 elog 2 esin 2r2p(y) ry21T p(xy)dxr2 y21222

27、 dxryrO 222 y2(rr y r)p(y) P(x)Hc(Y)Hc(X) 10g2Hc(XY)p(xy)logR1r - log2e bit/symbolp(xy)dxdylogp(xy)log1 .dxdy rlog 22 rR2rp(xy)dxdyIc(X;Y)Hc(X)210g 2 r log 2bit/symbolHc(Y) Hc(XY)210g2 e log rlog 2e bit/symbol某一无记忆信源的符号集为0,1,已知P(0)= 1/4, P(1)= 34(1)求符号的平均嫡；(2)有100个符号构成的序列，求某一特定序列(例如有 m个“0”和(100 -m)个

28、"1”)的自信息量的表达式;(3)计算(2)中序列的嫡。解：H(X)1.13,3p(xi )log p(xi) log log 0.811 bit / symbol44 44P(Xi) I (Xi)m100m100 m1331004443100 mlog p(xi)log100-41.5 1.585m bit4(3) H (X100) 100H(X) 100 0.81181.1 bit / symbol2-26口仙尸11P(i)= 51H(IJ尸P(ij尸3883111110 13 15 10J_ J_ J_ J_<36 12 36 364-Lo 炭颍 + 2- - -Logi

29、nj + 2Logl 5 + 3L 口或 2可 + Lo£l m=3.415有一个一阶平稳马尔可夫链X1,X2,L ,Xr,L ,各Xr取值于集合Aa1,a2,a3 ,已知起始概率P(X)为pi 1/2, p2 p3 1/4,转移概率如下图所示V12311/21/41/42Z301/33Z31/30求(X1, X 2, X 3)的联合嫡和平均符号嫡(2)求这个链的极限平均符号嫡求H 0,Hi,H 2和它们说对应的冗余度解：(1)H (X1,X2,X3) H(X1) H (X2|X1) H(X3|X2，X1)H (X1) H(X2|X1) H (X3|X2)111111H (X1)-l

30、og-log-log -1.5bit/符号224444X1, X2的联合概率分布为P(X1iX2j)12311/41/81/821/601/1231/61/120P(X2j)P(4X2j) iX2的概率那么12314245/245/24分布为111131131H (X21 Xi)log 4 log4 log 4 log log3 log log348862126212书号X2X3的联合概率分布为P(X2iX3j)1231力2474874825/3605/1235/363120那么H (X3|X2)7.-7,1 .5,35,八 5,35,八log 210g 4 log 4 log log3 lo

31、g log324488362 72362 72书号H (X1,X2,X3) 1.5 1.209 1.26 3.969bit/符号所以平均符号嫡H3(X1,X2,X3) 言9 1.323bit/符号(2)设ai,a2,a3稳定后的概率分布分别为 W1,W2,W3,转移概率距阵为P122323上WP W /i由Wi 1得到1224-W1-W2W31W123371W1V3W2计算得到W23_4314W1W2 W31W3314又满足不可约性和非周期性LVH (X)34WiH (X |Wi)Hi 171 1 1(2,4,4)3H 142 13,3,0)1.25bit /符号H0log3 1.58bit/

32、符号Hi1.5bit / 符号H21.251 1.580.21 11.251 0.6171.51.5 1.209舛口 1.355bit / 付节21.2512 1 0.0781.3552/31/41/42/3a2 1- a3 1/32-30(1)求平稳概率P(j/i)=H(S/s1)= -Log - + - Lug=0513331H(S/s2)= 0信源嫡为：H(S)=W1 H (S/s1)4W2-051S + 1-0 = Q.6SS442-311413P(j/i)=13 312解方程组rWPW2rwrmi町得到W1= -，W2= I1,W3= 4W1 + W2 + WJ = 1H(X2Z a

33、)= L 口忒今=1.583H»(X)=WE(X2咐+WzHK/bHW3H州化户-Lo3) + - LO0：3) + -Log(2) = 1439?34-一阶马尔可夫信源的状态图如图 213所示，信源X的符号集为(0, 1, 2)(1)求信源平稳后的概率分布P(0),P(1),P(2)(2)求此信源的嫡(3)近似认为此信源为无记忆时，符号的概率分布为平稳分布。求近似信源的嫡H(X)并与H进行比较1-p解:根据香农线图，列出转移概率距阵1 p p/2 p/2p/21 pp/2p/2p/2令状态0,1,2平稳后的概率分布分别为W1,W2,W3WP W3W 1i 1得到(1 p)W1 W2

34、pW1 (1 p)W2W1 W2 W3 1W32-W32W1W2计算得到131313由齐次遍历可得1.2Plog-1 P Puv(X)存在极大值uvuv1p pH (X)WiH (X |Wi) 3 H (1 p,p,-) (1 P)logi32 2H(X,) log 3 1.58bit/符号由最大嫡定理可知 或者也可以通过下面的方法得出存在极大值lvH (X)Plog(1 P)1),P 210g 2 P710g七P2(1 P)12(1 P)1所以2(1 P)0,当 p=2/3时12(1 P)uv0<p<23 时 H (X)Plog2(1 P)uvZ3<p<1 时 H (

35、X)Plog2(1 P)所以当uvuvP=23时H (X)存在极大值，且H (X) max1.58bit/符号uv(X) H(X,)0 -p) W1 + p = W12-33ri -P op i -t>L 0 P解方程组:p-WL + (1 - p)踞=W3P(0)=P(1)=P(2)=-)=H(X/1 )= H (X/2)= -1 - p) Log(l - p) -p Lo gfp)闵二二*H(X口 -+ 二“H凶】H *H(X/2)= p)-Log(l - p) p Log(p) 当p=0或p=1时信源嫡为0练习题：有一离散无记忆信源，具输出为X 0,1,2，相应的概率为p0 1/4

36、,pi 1/4,p2 1/2,设计两个独立的实验去观察它，其结果分别为Y1 0,1 ,丫2 0,1 ,已知条件概率：P(y1 |x)01012101/2111/2求I(X;Y1)和I(X;Y2),并判断哪一个实求I(X;Y1Y2),并计算做丫1和*两个实P(y2|x)01010110验好些201验比做0101/40101/421/41/42和Y2中的一个实验可多得多少关于 X的信息(3)求I (X;Y1|Y2)和I(X;Y2|Y1),并解释它们的含义解：(1)由题意可知P(y1=0)=p(y1=1)=1/2p(y2=1)=p(y2=1)=#21111I(X;Y1) H (Y1) H(Y1|X)

37、 log 2 log log 一42 42书号111I(X;Y2) H(Y2) H (Y2| X) log 2 Tog1 Tog1 Tog1 1bit /符号I (X ;Y1) 442所以第二个实验比第一个实验好(2)因为 Yi 和 丫2 相互独立，所以 p(y1y2|x) p(y1 |x) p(y2| x)1 . logi4i , , i -logi - 210g 244由此可见，做两个实验比单独做Yi可多得1bit的关于X的信息量，比单独做Y2多得的关于X的信息量(3)I(X;Yi|Y2) H(X|Yi) H(X|Yi,Y2)H(X,Y2)H(X) H(X) I(X;Yi,Y2)H (X)

38、 I(X;Y2) H (X) I(X;Yi,Y2)I (X;Yi,Y2) I (X;Y2)=W号表示在已做Y2的情况下，再做Yi而多得到的关于X的信息量同理可得I(X;Y2|Yi) I(X;Yi,Y2)I(X;Yi)=符号表示在已做Yi的情况下，再做Y2而多得到的关于X的信息量欢迎下载!第三章设二元对称信道的传递矩阵为31323(1)若 P(0) = 34, P(1) = 1/4,求 H(X), H(X/Y), H(Y/X和 I(X;Y);(2)求该信道的信道容量及其达到信道容量时的输入概率分布; 次：1)H(X)P(Xi)/3 ,3(4 log24110g 2 4)0.811 bit / s

39、ymbolH(Y/X)p(Xi)p(yj /Xi)log p(yj /为)p(y1)p(y2)H(Y)(30.918p(xiYi)p(XiY2)I(X;Y)H (X /Y)I(X;Y)lg3 331,111, 1lg lg4 3343 31 2. 2 .“lg-) 10g 2104 3 3bit/symbolp(x2y1) p(x)p(y1 / Xi)pdy?) p(x1)p(y2/x1)p(yj)(0.5833 log2 0.5833H(X)H(X)H(X)H (X /Y) H (Y)H (Y) H(Y/X)H (X /Y)0.811pM)p(y1 /X2)p(X2)p(Y2/x2)0.41

40、67H(Y/X)0.811 0.9800.749 0.0623434log2 0.4167)2313141410.583332 0.416730.980 bit / symbol0.918 0.749 bit/symbol bit/symbol2)C maxI (X;Y)1122log2 m Hmi log2 2 (-lg- -lg) log 210 0.082 bit / symbol 其取佳输入分 3 3 33布为p(xi)123-2某信源发送端有2个符县Xji=1, 2; p(Xi) a,每秒发出一个符号。接受端有 3种符号yi, j=1, 2, 3,转移概率矩阵为P1/ 2 1/2 0

41、O1/ 2 1/4 1/4(1)(2)(3)解:计算接受端的平均不确定度；计算由于噪声产生的不确定度 H(Y|X)计算信道容量。1/2 1/2 0P1/2 1/4 1/4联合率p(Xi, yj)X、YYiY2YbXia/2a/20X2(1 a)/2(1 a)/4(1 a)/4则Y的概率分布为Yy1y2y31/2(1 a)/4(1 a)/41(1) H(Y) 210g21 a ,4log41 a1 + a710g110g 21log 23 log 21 -1og 411 -1og16110g 41162a1a log141410g410g取2为底3H(Y) (2 410g2 H(Y|X)11a2

42、a.210ga log 2 "I ' log 23 al c 10g2取2为底3 aH (Y | X)bit 2c max I (X; Y) p(x),a1 ,1(ln 2 ln 24 1a1 1n2211n 2211n 22=01 a1 a1 2a41 a2a2(111n 43512aa410gaa1 alog 2 )bit41a1a.11a.1log - log 22222 max H (Y) H (Y | X) maxP(Xi)p(x)a, 1 a、 ln ) a 4 1a1 ln4Slog144Slog441og 2 - 10g2411 a2初旨取e为底a2)1 a1

43、1n 4a4(a41 a21一)a3 510g21一1og 2 - 10g1041 410g2511 253163 ,八 1 .51og 2 1og 102415_ 1og 24-1og 一2041og 21031log 54在有扰离散信道上传输符号1,在传输过程中每100个符号发生一个错误，已知P(0)=P(1)=/12,信源每秒内发出1000个符号，求此信道的信道容量解:由题意可知该二元信道的转移概率矩阵为:为一个BSC信道0.99 0.01 P0.01 0.99所以由BSC言道的信道容量计算公式得到:C logs H(P)log2Pi log 0.92bit/signPi920bit /

44、sec八 1八八Ct -C 1000C t求图中信道的信道容量及其最佳的输入概率分布.并求当e=0和1/2时的信道容量C的大小。XY1b- 00100解：信道矩阵P=0 1 e e ，此信道为非奇异矩阵，又尸S,可利用方程组求解 0e1 e33? P(bj|a)bj=? P(bj |a)log P(bj|a)(i=1,2,3)j= 1j= 1b1 = 0+ b M(借 e + s2角 1-bd e(1- e)log(1 - e) + elog e e log e+ (1- e)log(1 - e)b2 = b3 = (1- e)log(1 - e)+ elog e所以C=log? 2bj =log20+2X2(1-e)l0g(1-e)+eloge=log1+21-H(e)=log1+2(1- e)(1-e) eeP(b1)= 2b1-C = 2- CPM)= 2b2-C1_11+2(1- e)(1-e)ee 1+ 21- H (1- e)eee(1- e) e1+ 2(1- e)( )eP(b3)= 2b3-C= P(b2)3而 P(bj)= ? P(ai)P(bj 0)(j=1,2,3)?P(bJ= P(aJ得?P(b2)= P(a2)(1- e)+ P(