心理统计学-回归分析

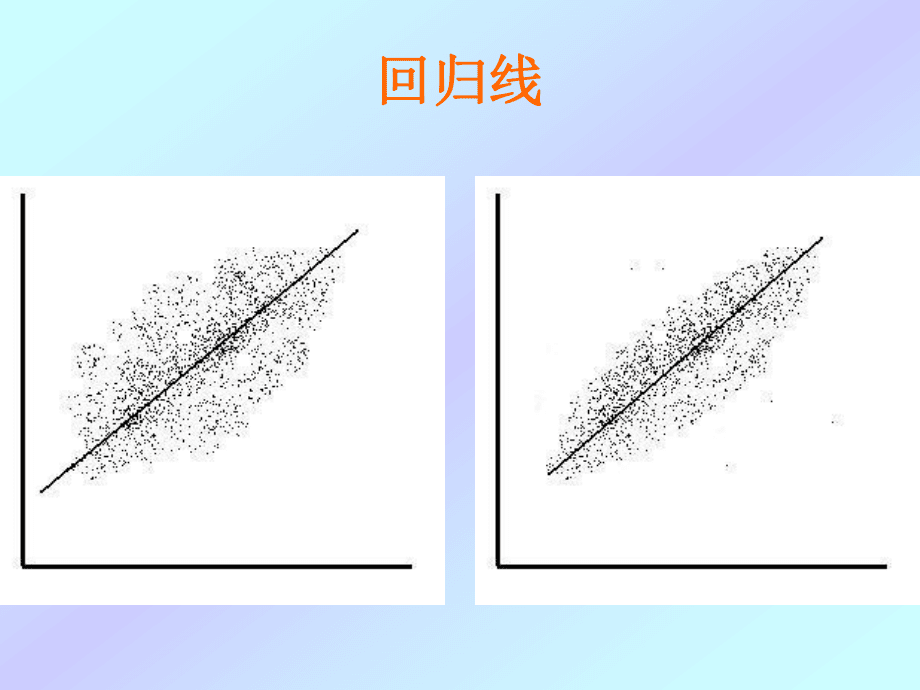
1、回归分析回归分析 相关系数双向关系相关系数双向关系 回归方程单向关系回归方程单向关系 一元线性回归一元线性回归 一元线性回归方程的检验一元线性回归方程的检验 一元线性回归方程的应用一元线性回归方程的应用 多元线性回归简介多元线性回归简介一元线性回归一元线性回归 一元线性回归是指只有一个自变量的线一元线性回归是指只有一个自变量的线性回归性回归(linear regression)。 回归线回归线(regression line) 一条最能代表散点图上分布趋势的直线，这一条最能代表散点图上分布趋势的直线，这条最优拟合线即称为回归线。条最优拟合线即称为回归线。 常用的拟合这条回归线的原则，就是使各点

2、常用的拟合这条回归线的原则，就是使各点与该线纵向距离的平方和为最小。与该线纵向距离的平方和为最小。 回归线回归线回归线回归线回归线回归线回归线回归线回归方程回归方程 确定回归线的方程称回归方程。确定回归线的方程称回归方程。bXaYXbaYYXYXYbaXXYXY回归方程的建立回归方程的建立 用最小二乘方法求回归系数用最小二乘方法求回归系数(regression coefficient)nXXnYXYXXXYYXXbniiniiniininiiiiniiiniiYX/)(/ )( )()()( )(2112111121与相关系数与相关系数 r 比较比较YXniiiSnSYYXXr1)(回归方程的

3、建立回归方程的建立 求截距求截距(intercept)XbYaYXYX由由Y估计估计XnYYnYXYXYYYYXXbniiniiniininiiiiniiiniiXY/)(/ )( )()()( )(2112111121YbXaXYXY语文成绩与智商语文成绩与智商 序号序号X Y X2 Y2 XY 1234567891011 7871688575737265706674 136135120140130128122118119108120 60845041462472255625532951844225490043565476 1849618225144001960016900163841488

4、413924141611166414400 1060895858160119009750934487847670833071288880 总和总和7971376 58069 173038 100139计算计算368. 111/7975806911/1376797100139/)(/ )( )(22112111nXXnYXYXbniiniiniininiiiiYX96.2545.72368. 109.125XbYaYXYXXY368. 196.25一元线性回归方程的检验一元线性回归方程的检验 三种等效的方法：三种等效的方法： 对回归方程进行方差分析对回归方程进行方差分析 对两个变量的相关系数进行

5、与总体零相关的对两个变量的相关系数进行与总体零相关的显著性检验；显著性检验； 对回归系数进行显著性检验。对回归系数进行显著性检验。测定系数测定系数 回归平方和回归平方和(regression sum of squares, explained ) 残差平方和残差平方和(residual sum of squares, error , unexplained )niiiniiniiYYYYYY121212)()()(测定系数测定系数 测定系数测定系数(coefficient of determination)指指回归平方和在总平方和中所占比例，这回归平方和在总平方和中所占比例，这个比例越大，意味

6、着误差平方和所占比个比例越大，意味着误差平方和所占比例越小，预测效果就越好。测定系数同例越小，预测效果就越好。测定系数同时等于相关系数的平方。时等于相关系数的平方。niiniiYYYYr12122)()(例题例题企业企业12345678910产量产量(X)40424855657988100 120 140费用费用(Y)150140160170150162 185 165 190 185XY3978. 07909.1346524.01000.25543577.1666)()(12122niiniiYYYYr对回归方程的方差分析对回归方程的方差分析方差来源方差来源平方和平方和自由度自由度均方差均方

7、差F 值值回归回归SSR1MSRMSR/MSE残差残差SSEn - 2MSE总差异总差异SSTn - 1) 2, 1 (221212) 2/()1 () 2/()()(nniniFnrrFnYYYYF或方差分析方差分析 F 0.05,1,8 = 5.32 F 0.01,1,8 = 11.3方差来源方差来源平方和平方和自由度自由度均方差均方差F 值值回归回归1666.357711666.357715.0166残差残差887.74238110.9678总差异总差异2554.10009对回归系数进行显著性检验对回归系数进行显著性检验 估计误差的标准差估计误差的标准差 由于与由于与 X 各点相对应的诸

8、各点相对应的诸 YX 值之平均数和值之平均数和标准差均为未知，故估计误差的标准差只能标准差均为未知，故估计误差的标准差只能从样本加以估计。其无偏估计量为：从样本加以估计。其无偏估计量为：212nYYSniiiYX对回归系数进行显著性检验对回归系数进行显著性检验 在回归线上，当与所有自变量在回归线上，当与所有自变量X相对应的相对应的各组因变量各组因变量Y的残值都呈正态分布，并且的残值都呈正态分布，并且残值方差为齐性时，可以用以下公式进残值方差为齐性时，可以用以下公式进行显著性检验。行显著性检验。 公式公式)2/()()()()(012121212nYYXXbSXXbXXSbSbtniiiniiY

9、XYXniiYXniiYXYXbYXYX一元线性回归方程的应用一元线性回归方程的应用 用样本回归方程推算因变量的回归值用样本回归方程推算因变量的回归值 点估计：点估计：语文成绩为语文成绩为8080分的学生的智商是多少分的学生的智商是多少？ 区间估计：区间估计：体重为体重为2020千克的男童的简单反应时千克的男童的简单反应时95%95%的置信区间的置信区间 =（5501.9693.67）=（550183.6）或或（366.4，733.6） 00XbaYYXYXYXnStY2, 2/4 .13580368. 196.25368. 196.2500XY一元线性回归方程的应用一元线性回归方程的应用 对

10、因变量真值的预测对因变量真值的预测 回归方程是由样本数据列出的，由于抽样误回归方程是由样本数据列出的，由于抽样误差的影响，其回归值并不是因变量的真值。差的影响，其回归值并不是因变量的真值。要预测其真值还需考虑到各样本回归方程之要预测其真值还需考虑到各样本回归方程之间的变异。间的变异。对因变量真值的预测对因变量真值的预测二元线性回归方程二元线性回归方程 二元线性回归方程是指一个因变量二元线性回归方程是指一个因变量Y与两与两个自变量个自变量X1与与X2之间建立的线性回归方之间建立的线性回归方程。程。 二元线性回归方程也用最小二乘法来确二元线性回归方程也用最小二乘法来确定回归系数。定回归系数。221

11、1XbXbaY 式中各个式中各个L都是相应的离差平方和或离差都是相应的离差平方和或离差乘积和乘积和二元线性回归方程的偏回归系数二元线性回归方程的偏回归系数21222111222211LLLLLLLbYY21222112111122LLLLLLLbYY例题例题序号序号数学成绩数学成绩Y学习能力学习能力X1逻辑学逻辑学X212345678910836774487266905471658868766074578662634575476057796367587069答案答案21413. 0606. 0214. 1XXY二元线性标准回归方程二元线性标准回归方程 为了比较两个自变量在估计预测因变量为了比较

12、两个自变量在估计预测因变量时所起作用的大小，需要将三个变量分时所起作用的大小，需要将三个变量分别转换成标准分数，然后比较由标准分别转换成标准分数，然后比较由标准分数所建立的标准回归方程中的两个标准数所建立的标准回归方程中的两个标准回归系数，以此判断两个自变量作用的回归系数，以此判断两个自变量作用的大小。大小。2121316.0655.0*2*1XXXXYZZZbZbZ二元线性回归的检验二元线性回归的检验 二元线性回归的检验二元线性回归的检验 检验回归方程的显著性检验回归方程的显著性 检验两个偏回归系数的显著性检验两个偏回归系数的显著性二元线性回归的检验二元线性回归的检验 二元线性回归方程的显著

13、性检验方法：二元线性回归方程的显著性检验方法： 方差分析方差分析 复相关系数复相关系数(multiple correlation coefficient)显著性检验。显著性检验。 复相关系数表示两个自变量组合起来与因变量之复相关系数表示两个自变量组合起来与因变量之间的相关程度。可通过对二元测定系数开平方根间的相关程度。可通过对二元测定系数开平方根得到，然后通过查表进行显著性检验。得到，然后通过查表进行显著性检验。niiniiYYYYYR1212122)()(二元线性回归的检验二元线性回归的检验 偏回归系数偏回归系数(partial regression coefficient)的显著性检验的显

14、著性检验)1 (0)1 (021222221211121rLMSEbtrLMSEbtbb3)(12nYYMSEniii多元线性回归方程多元线性回归方程pYpppppYppYppLLbLbLbLLbLbLbLLbLbLb.22112222221111122111ppXbXbXbYa.2211多元线性回归方程中自变量的选择多元线性回归方程中自变量的选择 穷举法穷举法 对所有可能的回归方程逐一检验，选择一个显著性对所有可能的回归方程逐一检验，选择一个显著性程度最强的方程。程度最强的方程。 逐步回归逐步回归(step-wise regression) 逐步回归的原理是按每个自变量对因变量的作用，逐步回归的原理是按每个自变量对因变量的作用，从大到小逐个地引入回归方程从大到小逐个地引入回归方程 每引入一个自变量要对回归方程中的每一个自变量每引入一个自变量要对回归方程中的每一个自变量都进