高中数学导数及其应用章末复习课 苏教版选修22

1、【创新设计】2016-2017学年高中数学 第一章 导数及其应用章末复习课 苏教版选修2-2题型一用导数求曲线的切线方程利用导数求切线方程时关键是找到切点，若切点未知需设出常见的类型有两种，一类是求“在某点处的切线方程”，则此点一定为切点，易求斜率进而写出直线方程即可得；另一类是求“过某点的切线方程”，这种类型中的点不一定是切点，可先设切点为Q(x1，y1)，由f(x1)和y1f(x1)求出x1，y1的值，转化为第一种类型例1已知函数f(x)xaln x(aR)(1)当a2时，求曲线yf(x)在点A(1，f(1)处的切线方程；(2)求函数f(x)的极值解函数f(x)的定义域为(0，)，f(x)

2、1.(1)当a2时，f(x)x2ln x，f(x)1(x>0)，因而f(1)1，f(1)1，所以曲线yf(x)在点A(1，f(1)处的切线方程为y1(x1)，即xy20.(2)由f(x)1，x>0知：当a0时，f(x)>0，函数f(x)为(0，)上的增函数，函数f(x)无极值；当a>0时，由f(x)0，解得xa.又当x(0，a)时，f(x)<0，当x(a，)时，f(x)>0，从而函数f(x)在xa处取得极小值，且极小值为f(a)aaln a，无极大值综上，当a0时，函数f(x)无极值；当a>0时，函数f(x)在xa处取得极小值aaln a，无极大值跟踪

3、训练 1已知函数f(x)ax22ln(2x)(aR)，设曲线yf(x)在点(1，f(1)处的切线为l，若l与圆C：x2y2相切，求a的值解依题意有：f(1)a，f(x)2ax(x<2)，l的方程为2(a1)xy2a0，l与圆相切，a，a的值为.题型二用导数求函数的单调区间求解函数yf(x)单调区间的步骤：(1)确定函数yf(x)的定义域；(2)求导数yf(x)；(3)解不等式f(x)>0，解集在定义域内的部分为增区间；(4)解不等式f(x)<0，解集在定义域内的部分为减区间特别要注意定义域，写单调区间时，区间之间用“和”或“，”隔开，绝对不能用“”连结例2求下列函数的单调区间

4、：(1)f(x)(x3)ex，x(0，)；(2)f(x)x(xa)2.解(1)f(x)(x3)ex(x3)(ex)(x2)ex，令f(x)>0，解得x>2，又x(0，)，函数的单调增区间为(2，)，函数的单调减区间为(0,2)(2)函数f(x)x(xa)2x32ax2a2x的定义域为R，由f(x)3x24axa20，得x1，x2a.当a>0时，x1<x2.函数f(x)的单调递增区间为(，)和(a，)，单调递减区间为(，a)当a<0时，x1>x2，函数f(x)的单调递增区间为(，a)和(，)，单调递减区间为(a，)当a0时，f(x)3x20，函数f(x)的单调

5、递增区间为(，)，即f(x)在R上是单调递增的综上，a>0时，函数f(x)的单调递增区间为(，)和(a，)，单调递减区间为(，a)；a<0时，函数f(x)的单调递增区间为(，a)和(，)，单调递减区间为(a，)；a0时，函数f(x)的单调递增区间是(，)跟踪训练 2求下列函数的单调区间：(1)f(x)sin x，x0,2；(2)yxlnx.解(1)函数的定义域是0,2，f(x)cos x，令cos x>0，解得2k<x<2k(kZ)，当x0,2时，0<x<，或<x<2，令cos x<0，解得<x<，因此，f(x)的单调递增

6、区间是(0，)和(，2)，单调递减区间是(，)(2)函数的定义域是(0，)，f(x)ln x1，令ln x1>0得x>e1，因此，f(x)的单调递增区间是(e1，)，单调递减区间是(0，e1)题型三数形结合思想在导数中的应用1应用导数求函数极值的一般步骤：(1)确定函数f(x)的定义域；(2)解方程f(x)0的根；(3)检验f(x)0的根的两侧f(x)的符号若左正右负，则f(x)在此根处取得极大值；若左负右正，则f(x)在此根处取得极小值；否则，此根不是f(x)的极值点2求函数f(x)在闭区间a，b上的最大值、最小值的方法与步骤：(1)求f(x)在(a，b)内的极值；(2)将(1)

7、求得的极植与f(a)、f(b)相比较，其中最大的一个值为最大值，最小的一个值为最小值；特别地，当f(x)在(a，b)上单调时，其最小值、最大值在区间端点处取得；当f(x)在(a，b)内只有一个极值点时，若在这一个点处f(x)有极大(小)值，则可以断定f(x)在该点处f(x)有极大(小)值，则可以断定f(x)在该点处取得最大(小)值，这里(a，b)也可以是(，)例 3设<a<1，函数f(x)x3ax2b(1x1)的最大值为1，最小值为，求常数a，b.解令f(x)3x23ax0，得x10，x2a.f(0)b，f(a)b，f(1)1ab，f(1)1ab.因为<a<1，所以1a

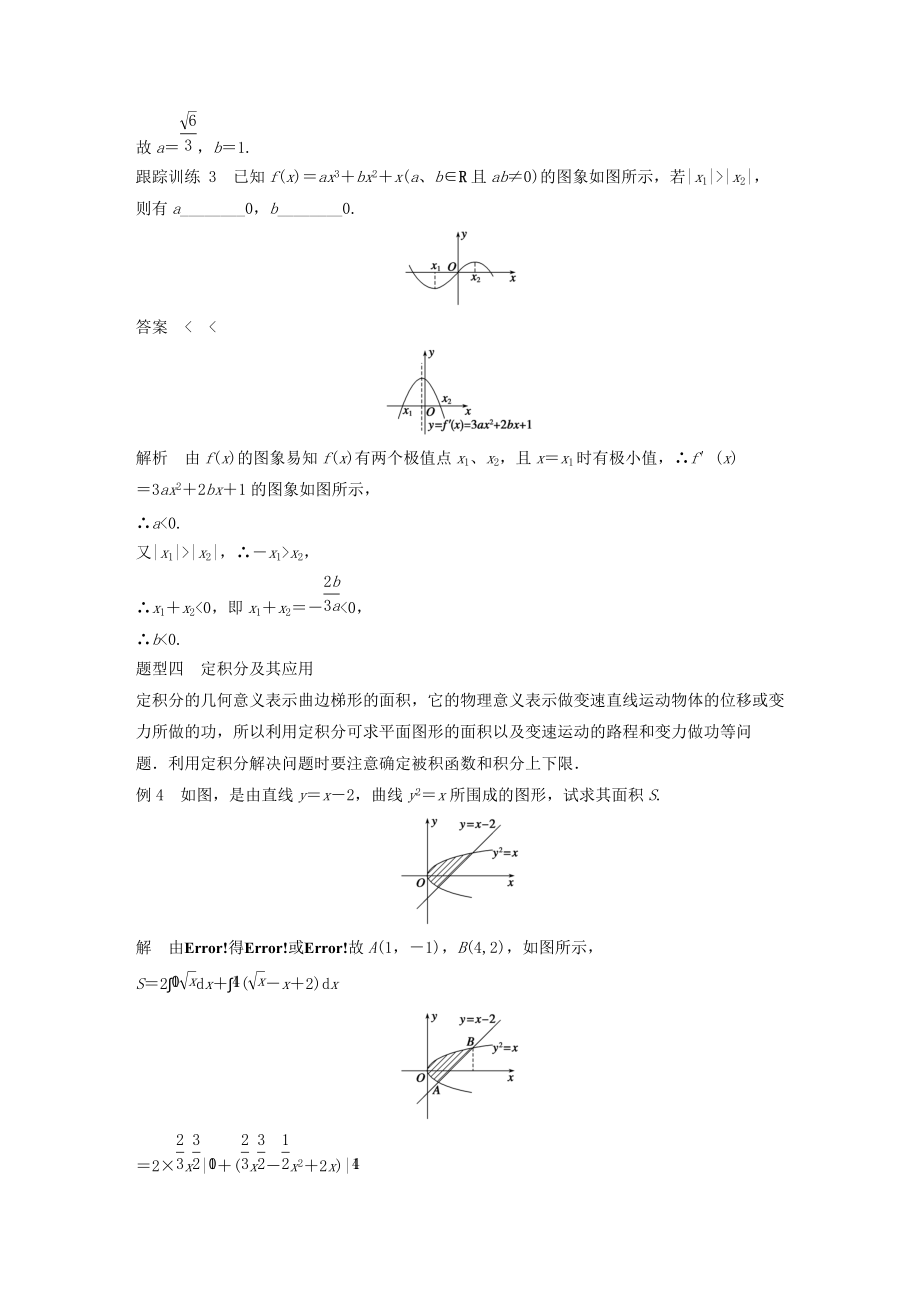
8、<0，故最大值为f(0)b1，所以f(x)的最小值为f(1)1aba，所以a，所以a.故a，b1.跟踪训练 3已知f(x)ax3bx2x(a、bR且ab0)的图象如图所示，若|x1|>|x2|，则有a_0，b_0.答案<<解析由f(x)的图象易知f(x)有两个极值点x1、x2，且xx1时有极小值，f(x)3ax22bx1的图象如图所示，a<0.又|x1|>|x2|，x1>x2，x1x2<0，即x1x2<0，b<0.题型四定积分及其应用定积分的几何意义表示曲边梯形的面积，它的物理意义表示做变速直线运动物体的位移或变力所做的功，所以利用定

9、积分可求平面图形的面积以及变速运动的路程和变力做功等问题利用定积分解决问题时要注意确定被积函数和积分上下限例4如图，是由直线yx2，曲线y2x所围成的图形，试求其面积S.解由得或故A(1，1)，B(4,2)，如图所示，S2dx(x2)dx2×x|(xx22x)|2×(×4×422×4)(2).跟踪训练 4在区间0,1上给定曲线yx2，如图所示，试在此区间内确定点t的值，使图中的阴影部分的面积S1与S2之和最小解面积S1等于边长为t与t2的矩形的面积去掉曲线yx2与x轴、直线xt围成的面积，即S1t·t2x2dxt3.面积S2等于曲线yx2与x轴，xt，x1围成的面积去掉矩形面积，矩形边长分别为t2，(1t)，即S2x2dxt2(1t)t3t2.所以阴影部分面积S为SS1S2t3t2(0t1)，由S(t)4t22t4t(t)0，得t0，或t.由于当0<t<时，S(t)<0；当<t<1时，S(t)>0，所以S(t)在0<t<上单调递减，在<t<1上单调递增所以当t时，S最小，即图中阴影部分的面积S1与S2之和最小呈重点、现规律1求函数中参数的取值范围问题，可以有两种类型：一是已知函数单调性(或极值)，求参数范围；二是已知函数最值(或恒成立)等性质，求参数范