上海中考数学初三相似三角形讲义2

1、第一课时相似三角形第一部分：概念梳理2015/8/53 / 111、相似形2、在四条线段中，如果其中两条线段的比等于另外两条线段的比，那么这四条线段叫做成 比例线段，简称比例线段.3、比例的性质：等比性质、合比性质4、黄金分割、重心5、三角形一边的平行线的性质定理6、三角形一边的平行线的判定定理7、相似三角形的判定预备定理：8、相似三角形的判定定理9、相似三角形的性质定理 10、向量的概念 11、向量的线性运算 12、向量的线性组合和分解第二部分：基础小测验（自己分配时间，也可以课下测验）（时间：20-30分钟，总分：100分，每题5分） 选择题1、东海大桥全长 32.5千米，如果东海大桥在某

2、张地图上的长为6.5厘米，那么该地图上距离与实际距离的比为（）.A. 1: 5000000; B. 1: 500000; C. 1: 50000; D. 1: 5000.2、根据你对相似的理解，下列命题中，不正确的是（）.（A）两个全等三角形一定相似；（B）两个等边三角形一定相似；（C）两个直角三角形一定相似；（D）两个正方形一定相似.a c3、如果一 一（其中b 0,d 0）,那么下列式子中不正确 的是（）b d. a b c d c a c cb d ' b d d4、下列四个命题中，真命题的个数为 ()(1)平行于三角形一边的直线截其他两边所在的直线，截得的三角形与原三角形相似；

3、(2)如果一个三角形的三条边与另一个三角形的三条边对应成比例，那么这两个三角形相似；(3)如果一个三角形的两边与其中一条边上的中线与另一个三角形的两边及其中一条边上的中线对应成比例，那么这两个三角形相似；(4)如果一个三角形的两边及第三边上的高与另一个三角形的两边及第三边上的高对应成比例，那么这两个三角形相似 .(A) 1 个；(B) 2 个；(C) 3 个； (D) 4 个.5.如图5,在 ABC中，点 D、E分别在边 AB、AC上,DE/BC, AD ： BD = 1 ： 2,那么Sa dbe : Sa cbe 等于()(C) 1 ： 4;(D) 1 ： 6.(A) 1 ： 2;(B) 1

4、 ： 3;6.已知非零向量m, n和单位向量e ,则下列等式中正确的是(A. me mB.C. en nD.7.如图, (A) (C)已知AC:CD:AB AE EF/ CD / EF , BD: DF 2: 5; (B) AB: CD 2: 5； (D) CE: EA2: 5, 2:5;5: 7.那么下列结论正确的是(8.如图,ABC 中,卜列结论正确的是(AB)AC3,BC 2,点D在月AC上，且BD BC ,那么(A) AD 2; (B)AD4CD ； 3(D) CD - 39、如图，梯形 ABCD的对角线 AC、BD相交于O, G是BD的中点.若 AD = 3, BC = 9 ,则 G

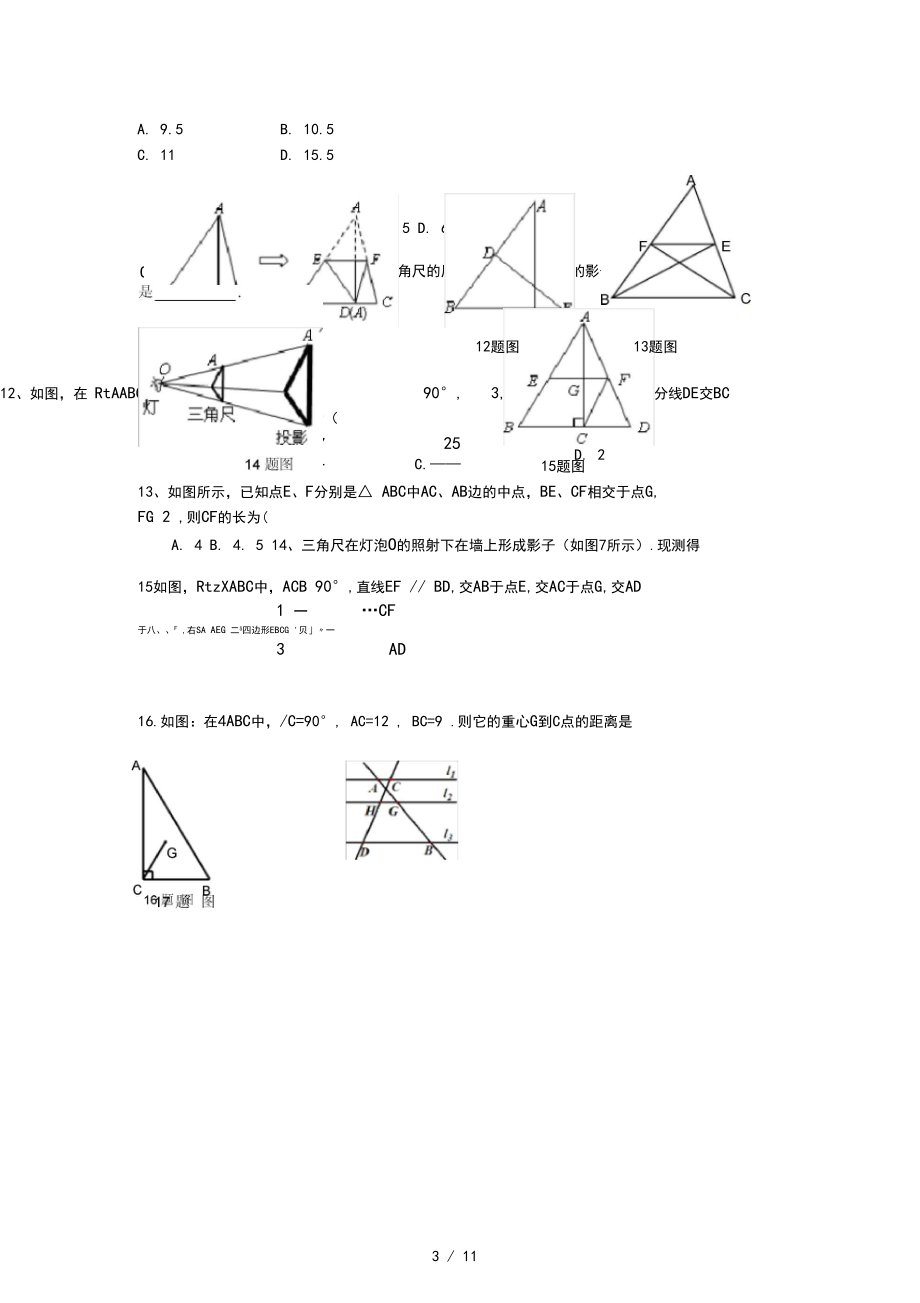
5、O : BG =().A. 1 : 2B. 1 : 3C. 2 : 3D. 11:2010、若ABCsDEF, AABC与ADEF的相似比为1 : 2,则ABC与4DEF的周长比为 ( )A.1：4 B.1：2 C, 2 ： 1D.1：V211、在AABC中，AB=12, AC=10, BC=9, AD是BC边上的高.将AABC按如图所示的方式折叠，使点A与点D重合，折痕为EF,则4DEF的周长为A. 9.5C. 1112题图13题图12、如图，在 RtAABC 中， ACB90°, BC3, AC的延长线于点E ,则CE的长为（7B.一625C.64, AB的垂直平分线DE交BCD

6、. 2B. 10.5D. 15.5)C. 5 D. 6OA 20cm, OA 50cm ,这个三角尺的周长与它在墙上形成的影子的周长的比15题图13、如图所示，已知点E、F分别是 ABC中AC、AB边的中点，BE、CF相交于点G,FG 2 ,则CF的长为(A. 4 B. 4. 5 14、三角尺在灯泡O的照射下在墙上形成影子（如图7所示）.现测得15如图，RtzXABC中，ACB 90°,直线EF / BD,交AB于点E,交AC于点G,交AD1 一CF于八、F ,右SA aeg 二S四边形EBCG '贝一3AD16.如图：在4ABC中，/C=90°, AC=12 ,

7、BC=9 .则它的重心G到C点的距离是 17.如图，直线 11/12/13,已知 AG = 0.6cm, BG = 1.2cm, CD = 1.5cm, CH =cmAB5 / 11第21题18.如图，已知在平行四边形ABCD中，点 E、F分别在线段 BD、AB上，EF /AD ,DE : EB=2 : 3, EF=9,那么 BC 的长为.19 如图，已知 AD/ EF/ BC,且 AE=2EB, AD=8 cm, AD = 8 cm, BC= 14 cm,点B', F, C为顶点的三角形与4ABC相似，若是.BFC20题图【请呗忘记总结回顾】AB=b,BC=a 那么 BF贝U S 梯

8、形 Ao EFD : S 梯形 BCFE =.20将三角形按照如图所示白方式折叠，使点 B落在边AC上，记为点B；折痕为EF.若以第三部分：综合题分析1、如图，在DE / BA.ABC中，点I如果CE=24,D、E分别在 BC、AC上，BE平分/ ABC, ，AE=26, AB=45,求 DE 和 CD 的长.17.如图，直线 11/12/13,已知 AG = 0.6cm, BG = 1.2cm, CD = 1.5cm, CH =cm18.如图，已知在平行四边形ABCD中，点 E、F分别在线段 BD、AB上，EF /AD ,DE : EB=2 : 3, EF=9,那么 BC 的长为AB第21题

9、6 / 1119 如图，已知 AD/ EF/ BC,且 AE=2EB, AD=8 cm, AD = 8 cm, BC= 14 cm,则 S梯形Ao EFD : S梯形BCFE =.20将三角形按照如图所示白方式折叠，使点B落在边AC上，记为点B；折痕为EF.若以点B', F, C为顶点的三角形与 4ABC相似，那么BF的长度是 .20题图【请呗忘记总结回顾】第三部分：综合题分析BE 平分/ ABC,1、如图，在 ABC中，点 D、E分别在 BC、AC上,DE / BA. 如果 CE=24, AE=26, AB=45,求 DE 和 CD 的长.2、已知，在4ABC中，点D、E分别在 AB

10、、AC上，且ADDBAEEC '已知S ADE1,S DBC 12 ,求 S ABC3、如图，在4AB中，D是AB的中点，过点 D的直线交边AC于E,交求证：变些CF ECBC的延长线于F,8 / 11，连接BD、BE,已知4、如图，在 ABC 中,AB=AC,D、E分别是 AC 及AC延长线上的点ac2=ad?ae ,求证：(1) AABDAAEB. (2) BC 平分 / DBE.5、已知：AD是RtAABC中/ A的平分线，/ C=90°, EF是AD的垂直平分线交AD于M,N。求证：(1) AMEsNMD(2) ND2=NC NBEF、BC的延长线交于一点6、在 AB

11、C 和 AED 中，AB AD = AC AE ,CAE = BAD，S ADE = 4 S ABC求证：DE = 2 BC.DE7、如图，M为线段AB的中点，AE与BD交于点C, / DME = / A= / B=" 且DM交AC于F, ME交BC于G.(1)写出图中三对相似三角形，并证明其中的一对；(2)连结 FG,如果 “=45°, AB=4&，AF=3,求 FG 的长.4 M E【关键词】直角三角形的有关计算、相似三角形有关的计算和证明【答案】(1)证： AMFsBGM, DMGsDBM, EMFseam (写出两对即可) 以下证明 AMFsBGM. / A

12、FM = / DME +Z E=Z A+Z E=Z BMG , / A= / B AMFA BGM .(2)解：当 a= 45°时，可得 AC，BC且AC=BC. M 为 AB 的中点，AM = BM=2jAF BM又 AMF s* BGM , AM BGAM gBM 2 2 2,2 8一 BG AF33又 AC BC 4服cos45o 4, . CGFG ,CF2 CG2 Ji2 (4)2 58、(本题12分)如图1,在平行四边形(1)求证： D ACB;(2)若点E、F分别为边BC、2分8 4c；4 - - , CF 4 3 1 3 3ABCD 中，AC CD.CD上的两点，且

13、EAFCAD.(如图2)求E C 证：ADF s ACE;求B/ A 证:AE EF .8/1-DFDAA（图（图1）39、如图，已知梯形 ABCD 中，ADBC, AB BC , AB 4 , AD CD 5, cot C -. 4点P在边BC上运动（点P不与点B、点C重合），一束光线从点 A出发，沿AP的方向射 出，经BC反射后，反射光线 PE交射线CD于点E .（1）当PE CE时，求BP的长度;（2）当点E落在线段CD上时，设BP x, DE y ,试求y与x之间的函数关系,并写出其定义域;13 / 11【请别忘记总结回顾】课外作业：1、（本题满分12分，每小题满分各 6分）如图，已知

14、：在 RtAABC 中，/ ACB=90° , AC=BC=4,中点，E、G分别是边 AC、BC上的一点，/EMG = 45° , AC与MG的延长线相交于点 F,(1)在不添加字母和线段的情况下写出图中一定相似的三角形，并证明其中的一对;(2)联结结 EG,当 AE=3时，求EG的长.2、(2009年义乌)如图，在矩形 ABCD, AB=3,AD=1,点P在线段AB上运动，设 AP=X ,现 将纸片折叠，使点 D与点P重合，得折痕EF (点E、F为折痕与矩形边的交点)，再将纸片 还原。(1)当X=0时，折痕EF的长为；当点E与点A重合时，折痕EF的长为 (2)请写出使四边形 EPFD为菱形的x的取值范围，并求出当 X=2时菱形的边长；(3)令EF2 y ,当点E在AQ点F在BC上时，写出y与x的函数关系式。当 y取最大值时，判断 EAP与4PBF是否相似？若相似，求出 X的值；若不相似，请说明理由。温馨提示：用草稿纸折折看，或许对你有所帮助哦!【关键词】相似三角形 【答案】解：(1) 3, 近(2) 1 < x< 3.2时，如图1,连接DE、PF ,Q EF为折痕，DE PE ,令PE为m ,则AE 2 m,在 RtzXADE 中，AD2 AE2 DE2,_221 (2 m) m ,解得5 5一,此时