北师大版本数学九上第二章（一元二次方程）复习教案

1、北师大版九年级(上) 第二章：一元二次方程1. 认识一元二次方程：概念：只含有一个未知数，并且可以化为 (为常数，)的整式方程叫一元二次方程。构成一元二次方程的三个重要条件：、方程必须是整式方程(分母不含未知数的方程)。如：是分式方程，所以不是一元二次方程。、只含有一个未知数。、未知数的最高次数是2次。2. 一元二次方程的一般形式：一般形式： ()，系数中，一定不能为0，、则可以为0，所以以下几种情形都是一元二次方程：、如果，则得，例如：；、如果，则得，例如：；、如果，则得，例如：；、如果，则得，例如：。其中，叫做二次项，叫做二次项系数；叫做一次项，叫做一次项系数；叫做常数项。任何一个一元二次

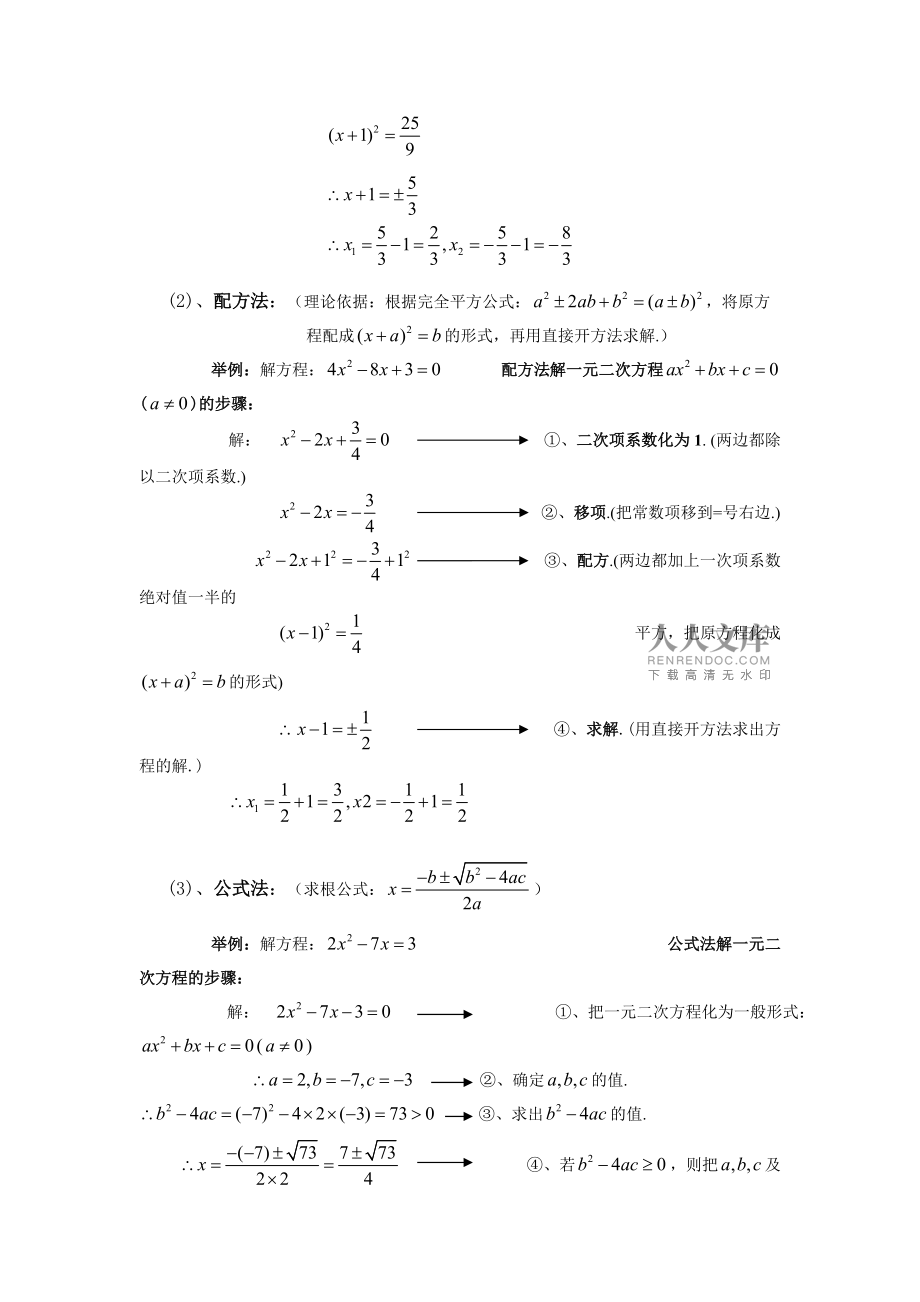
2、方程经过整理(去括号、移项、合并同类项)都可以化为一般形式。 例题：将方程化成一元二次方程的一般形式. 解： 去括号，得： 移项、合并同类项，得： (一般形式的等号右边一定等于0)3. 一元二次方程的解法：(1)、直接开方法：（利用平方根的定义直接开平方求一元二次方程的解） 形式： 举例：解方程： 解：方程两边除以9，得：(2)、配方法：（理论依据：根据完全平方公式：，将原方程配成的形式，再用直接开方法求解.）举例：解方程： 配方法解一元二次方程 ()的步骤： 解： 、二次项系数化为1. (两边都除以二次项系数.) 、移项.(把常数项移到=号右边.) 、配方.(两边都加上一次项系数绝对值一半的

3、 平方，把原方程化成的形式) 、求解.(用直接开方法求出方程的解.)(3)、公式法：（求根公式：） 举例：解方程： 公式法解一元二次方程的步骤：解： 、把一元二次方程化为一般形式：() 、确定的值. 、求出的值. 、若，则把及的值代入求 根公式，求出和，若，则方程无解。(4)、分解因式法：（理论依据：，则或；利用提公因式、运用公式、十字相乘等分解因式方法将原方程化成两个因式相乘等于0的形式。）【1】提公因式分解因式法：举例：、解方程： 、解方程： 解：原方程可变形为： 解：原方程可变形为： 或 或 【2】运用公式分解因式法：举例：、解方程： 、解方程： 解：原方程可变形为： 解：原方程可变形为

4、： 或 或 【3】十字相乘分解因式法(简单、常用、重要的一元二次方程解法)：举例：解方程：十字相乘法：1 -6 交叉相乘：， 1 +1 即等于一次项系数。所以可以分解成 解：原方程可变形为： 或【4】其它常见类型举例：、解方程： 、解方程： （换元法）解：原方程可变形为： 解：令，原方程可化为：，即： 或 或 ，即 ， 或，即 方程无解。 原方程的解为：4. 一元二次方程的应用：、数字问题.、面积问题.(牢记有关面积的公式，熟练计算组合图形的面积、面积的转化.)、平均增长率(或降低率)问题.其基本关系式：，其中是增长(或降低)的基础量，是平均增长(或降低)率，是增长(或降低)的次数（常考的是两

5、年期，即，），是增长(或降低)后的数量(总量)，增长为“+”，降低为“-”.、商品利润问题(重点).基本公式： 1、单件利润=单件进价 2、总利润=单件利润销售量、运动问题、动点问题。例题：将进货单价为40元的商品按50元售出时，能卖出500个，已知这种商品每个涨价1元，其销售量就减少10个。问：为了赚得8000元的利润，售价应定为多少？这时应进货多少个？ 解法一：设售价定为元，依题意可得： 整理得： 解得： 售价应定为60元或80元.当定为60元时，应进货个；当定为80元时，应进货个； 解法二：设上涨元，依题意可得： 整理得： 解得： 售价应定为10+50=60元或30+50=80元.当定为

6、60元时，应进货个；当定为80元时，应进货个；5. 常考题型及其相应的知识点：(1)、利用一元二次方程的一个已知根求系数及求另一个根问题： 例1：关于的一元二次方程有一根为0，则的值为_. 思路分析：有一根为0，说明有，可代入原方程求出. 注意：一元二次方程时刻不要忘记对二次项系数的讨论：解：将代入原方程得： 即： 又因为 即 的值为. 例2：一元二次方程 的一个根为，则另一个根为_. 思路分析：先将已知的一个根代入原方程，解出未知系数，再解出此时一元二次方程的两根. 解：将代入原方程得： 原方程即为： (2)、判别式：，方程根的情况： 判别式与一元二次方程根的情况： 方程有两个不相等的实数根. 方程有两个相等的实数根(或说方程有一个实数根). 方程没有实数根. 例1：关于的一元二次方程有实数根，则的取值范围是_. 思路分析：方程有实数根，但具体不知道有多少个根，所以有. 解： 因为方程有实数根， 即： 例2：方程的根的情况是( ). A、只有一个实数根. B、有两个相等的实数根. C、有两个不相等的实数根. D、没有实数根 思路分析：判别方程根的情况，之需要计算判别式的值与0比较. 解： 方程没有实数根，选择D. (2)、一元二次方程根与系数关系，韦达定理： 如果是一元二次方程 ()的两根，根据韦达定理，则有： 例1：已知一元二次方程的两根，则_，_. 解：