



版权说明:本文档由用户提供并上传,收益归属内容提供方,若内容存在侵权,请进行举报或认领
文档简介
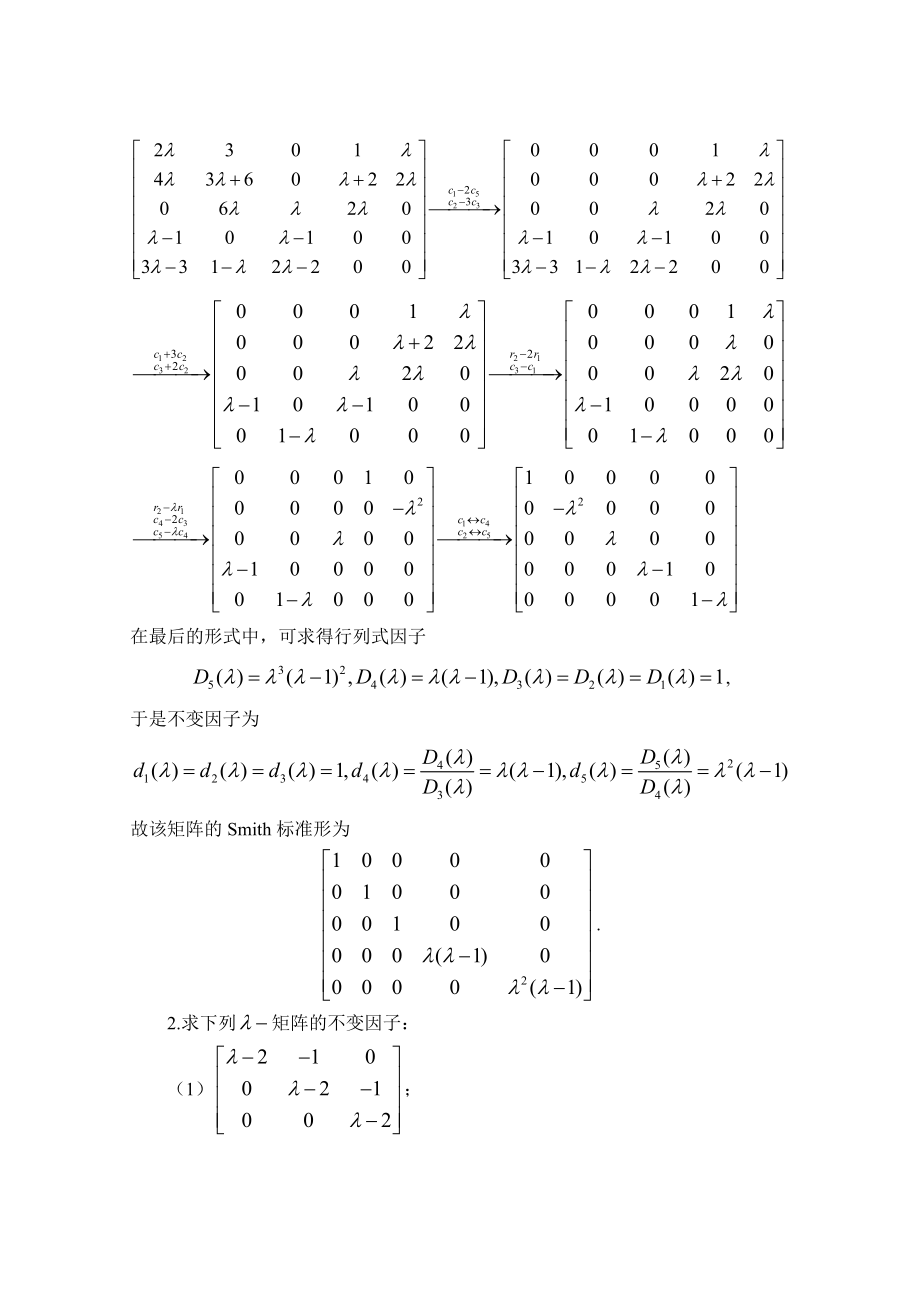
1、习题二1化下列矩阵为Smith标准型:(1);(2);(3);(4).解:(1)对矩阵作初等变换,则该矩阵为Smith标准型为;(2)矩阵的各阶行列式因子为,从而不变因子为故该矩阵的Smith标准型为;(3)对矩阵作初等变换故该矩阵的Smith标准型为;(4)对矩阵作初等变换在最后的形式中,可求得行列式因子,于是不变因子为故该矩阵的Smith标准形为.2.求下列矩阵的不变因子:(1);(2);(3);(4).解:(1)该矩阵的右上角的2阶子式为1,故而,所以该矩阵的不变因子为;(2)当时,由于,故不变因子为,当时,由于,且该矩阵中右上角的3阶子式为且,则,故,所以该矩阵的不变因子为;(3)该矩
2、阵的右上角的3阶子式为,故而,所以该矩阵的不变因子为 ;(4)该矩阵的行列式因子为,所以该矩阵的不变因子为.3求下列矩阵的初等因子:(1);(2).解:(1)该矩阵的行列式因子为,故初等因子为;(2) 该矩阵的行列式因子为,故不变因子为因此,初等因子为.4求下列矩阵的Jordan标准形:(1);(2);(3);(4);(5);(6).解:(1)设该矩阵为,则,故的初等因子为,则的Jordan标准形为;(2)设该矩阵为,则,故的初等因子为,从而的Jordan标准形为;(3)设该矩阵为,则,故的初等因子为从而的Jordan标准形为;(4)设该矩阵为,则,故的初等因子为,从而的Jordan标准形为;
3、(5)设该矩阵为,则,故的初等因子为,从而的Jordan标准形为;(6)设该矩阵为,则,该矩阵的各阶行列式因子为,则不变因子为,故初等因子为,则的Jordan标准形为.5设矩阵,求.解:矩阵的特征多项式为,故的特征值为,.属于特征值的特征向量为,属于的特征向量为.设,则.,故.6.设矩阵,求的Jordan标准形,并求相似变换矩阵,使得.解:(1) 求的Jordan标准形.,故其初等因子为,故的Jordan标准形.(2)求相似变换矩阵.考虑方程组即解之,得.其通解为=,其中为任意常数.考虑方程组,故当时,方程组有解.取,解此方程组,得.则相似变换矩阵.7.设矩阵,试计算.解: 矩阵的特征多项式为,由于,其中.且,故=.8.证明:任意可逆矩阵的逆矩阵可以表示为的多项式.证明:设矩阵的特征多项式为,则,即,因为可逆,故,则9.设矩阵,试计算.解: 矩阵的特征多项式为,则,而,故.10.已知3阶矩阵的三个特征值为1,1,2,试将表示为的二次式.解: 矩阵的特征多项式为,则设,由得解之,得,因此.11.求下列矩阵的最小多项式:(1);(2);(3)阶单位阵;(4)阶方阵,其元素均为1;(5).解:(1) 设,则,故该矩阵的最小多项式为.(2) 设,则,故该矩阵有三个不同的特征值,因此其最小多项式为(3) 阶
温馨提示
- 1. 本站所有资源如无特殊说明,都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
- 2. 本站的文档不包含任何第三方提供的附件图纸等,如果需要附件,请联系上传者。文件的所有权益归上传用户所有。
- 3. 本站RAR压缩包中若带图纸,网页内容里面会有图纸预览,若没有图纸预览就没有图纸。
- 4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
- 5. 人人文库网仅提供信息存储空间,仅对用户上传内容的表现方式做保护处理,对用户上传分享的文档内容本身不做任何修改或编辑,并不能对任何下载内容负责。
- 6. 下载文件中如有侵权或不适当内容,请与我们联系,我们立即纠正。
- 7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。

评论
0/150
提交评论