勾股定理 (3)

1、【学习课题】 八年级上册第章第1课时 勾股定理 【学习目标】1、经历用数格子的办法探索勾股定理的过程，进一步发展学生的合情推理意识，主动探究的习惯，进一步体会数学与现实生活的紧密联系。 【学习重点】了解勾股定理的由来并能用它解决一些简单问题理【学习难点】探索勾股定理ABCABC图1-1图1-2【学习过程】一、学习准备：1、我们知道，任意三角形的三条边必须满足定理：三角形的两边之和大于第三边。对于等腰三角形和等边三角形的边，除满足三边关系定理外，它们还分别存在着两边相等和三边相等的特殊关系。2、对于直角三角形的边，除满足三边关系定理外，它们之间还存在着一种很特殊的关系，这就是我们这一节要研究的问

2、题：勾股定理。二、解读教材：3、（1）观察图1-1, 正方形A中含有 个小方格，即A的面积是 个单位面积,正方形B的面积是 个单位面积, 正方形C的面积是 个单位面积.观察图1-2 A的面积是 个单位面积,正方形B的面积是 个单位面积, 正方形C的面积是 个单位面积.4、你是怎样求11中正方形C的面积的？（1）将正方形C分割成四个相同的直角三角形， = 。（2）在正方形C外部拚四成四个相同的直角三角形构成个边长为6的大正方形。= 。5、探索勾股定理（1）A、B、C间的面积之间有什么关系的？ 即：两条直角边上的正方形面积之和 斜边上的正方形的面积。（2）、由此我们得到：勾股定理（gou-guth

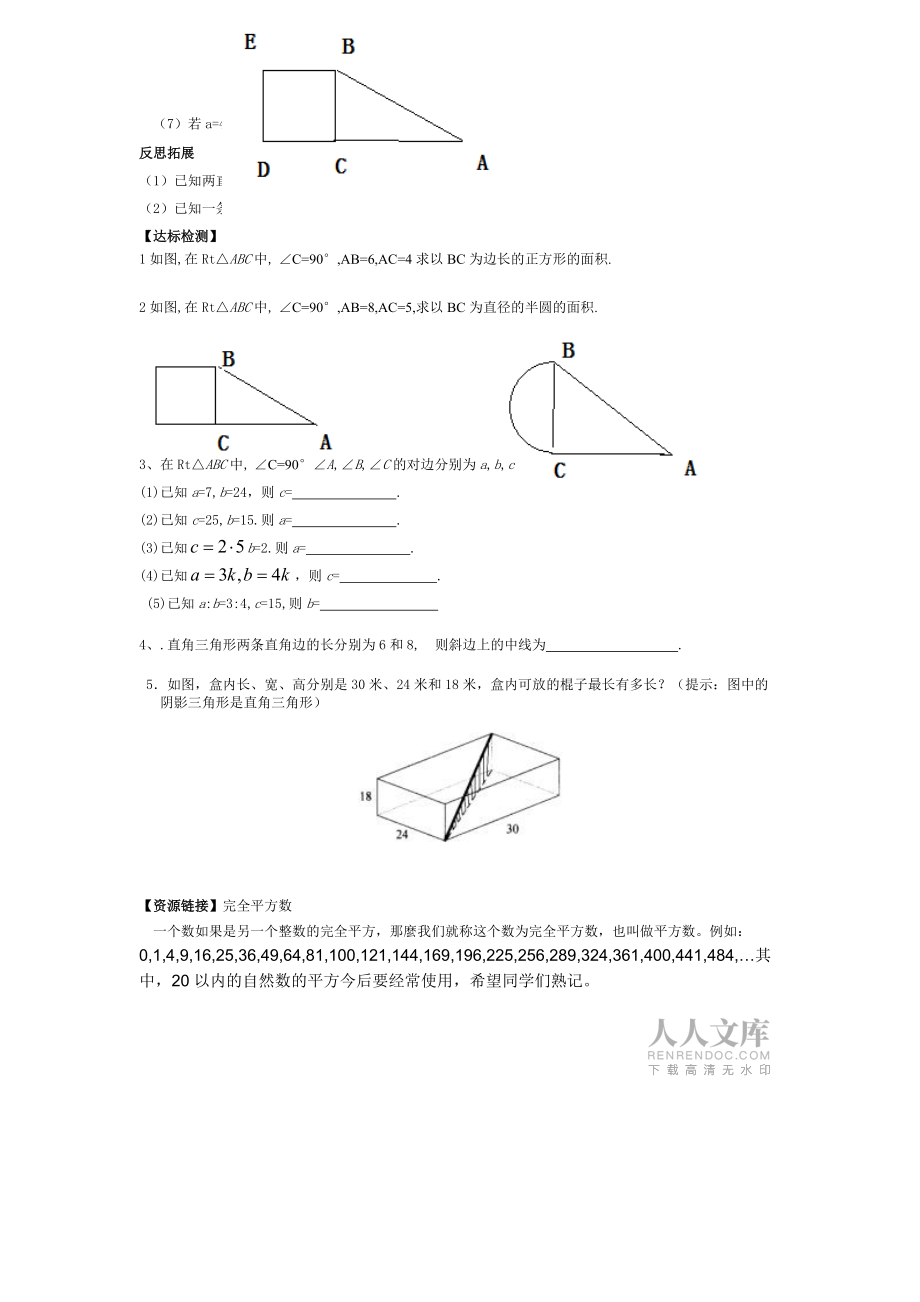
3、eorem)：直角三角形两直角边的 等于斜边的 。如图，如果直角三角形两直角边分别为a、b,斜边为c，那么 。cab即时练习1、如图，正方形A的面积是_2、已知在RtABC中，C=90°。（1）若a=3，b=4，则c=_；（2）若a=6，b=10，则c=_；（3）若a=5，b=12，则c=_。（4）若a=8，b=15，则c=_。（5）若a=1，b=1，则c=_。（6）若a=1，b=2，则c=_。（7）若a=4，b=9，则c=_。反思拓展（1）已知两直角边长，怎样求斜边长？（2）已知一条直角边长和斜边长，怎样求另一直角长？【达标检测】1如图,在RtABC中, C=90°,AB

4、=6,AC=4求以BC为边长的正方形的面积.2如图,在RtABC中, C=90°,AB=8,AC=5,求以BC为直径的半圆的面积.3、在RtABC中, C=90°A,B,C的对边分别为a,b,c(1)已知a=7,b=24，则c= .(2)已知c=25,b=15.则a= . (3)已知b=2.则a= . (4)已知，则c= . (5)已知a:b=3:4,c=15,则b= 4、.直角三角形两条直角边的长分别为6和8, 则斜边上的中线为 . 5如图，盒内长、宽、高分别是30米、24米和18米，盒内可放的棍子最长有多长？（提示：图中的阴影三角形是直角三角形）【资源链接】完全平方数一

5、个数如果是另一个整数的完全平方，那麼我们就称这个数为完全平方数，也叫做平方数。例如：0,1,4,9,16,25,36,49,64,81,100,121,144,169,196,225,256,289,324,361,400,441,484,其中，20以内的自然数的平方今后要经常使用，希望同学们熟记。【学习课题】 第2课时 拼图法验证勾股定理 【学习目标】1、经历运用拼图的方法说明勾股定理是正确的过程，在数学活动发展学生的探究意识和合作交流的习惯；2、经历用不同拼图方法验证勾股定理的过程，体验解决同一问题方法的多样性，进一步体会勾股定理的文化价值。【学习重点】能熟练应用拼图法证明勾股定理【学习难

6、点】如何拼图验证勾股定理cab【学习过程】学习准备： 1、学前准备：剪刀，四个全等的直角三角形，直尺。2、勾股定理（gou-gutheorem)：直角三角形两直角边的 等于斜边的 。3、如图，如果直角三角形两直角边分别为a、b,斜边为c，那么 。解读教材：1、阅读教材2、导入课题：利用拼图来验证勾股定理我们已经通过数格子的方法发现了直角三角形三边的关系，几个实例不具有普遍的意义，还需要加以论证，下面就是今天所要研究的内容，下边请大家画四个全等的直角三角形，并把它剪下来，（设直角三角形的两条直角边分别为a，b，斜边为c），用这四个直角三角形拼一拼、摆一摆，看看能否得到一个含有以斜边c为边长的正方

7、形，并与同学交流。3、你能否就你拼出的图说明a2+b2=c2？交流讨论：4、交流讨论：如左图：大正方形的面积可以表示为 ；也可以表示为 。 c2= 4×ab +(b-a)2 =2ab+b2-2ab+a2 =a2+b2a2+b2= c2如右图：大正方形的面积可以表示为 ；也可以表示为 。 (a+b)2 = c2+4×ab a2+2ab+b2 = c2 +2aba2+b2= c2这就可以从理论上验证了勾股定理的正确性。拼图法证明：以下是几种用拼图法证明勾股定理的方法，请你以小组合作的形式加以说明。图（2）图（1）方法一：图1中，甲的面积 (大正方形面积) ( 4个直角三角形面积

8、)。图2中，乙和丙的面积和(大正方形面积)( 4个直角三角形面积)。因为图1和图2的面积相等，所以甲的面积乙的面积丙的面积 c2 a2 b2   方法二：“青朱出入图”（兴趣题） 方法三：自己试试看.方法四： 方法五：【资源链接】常用勾股数的求解方法：满足的三个正整数，称为勾股数。我们已经知道以n2-1、2n、n2+1(n>1)为边长的三角形是直角三角形，当n分别取2、时就得到勾股数：（）、；（）、；（）、；（）、；（）、；（）、。其中（）、（）分别除以为、；、。它们与（）、（）、（）、（）会经常使用。【学习课题】 第3课时 勾股定理应用【学习目标】会用勾股

9、定理解决与直角三角形有关的计算问题.【学习重点】正确使用勾股定理并能正确快速运算.【学习难点】适当添加辅助线构建直角三角形，选择恰当未知数列方程。【候课朗读】在直角三角形中,(1)两条直角边的平方和等于斜边的平方;(2) 30°角所对直角边等于斜边的一半.【学习过程】一、学习准备：1、填空：在，= ， ，则= 。（1） 。（2） 。（4） 。二、解读教材：2、特殊直角三角形问题例1已知在RtABC中，C=90°，A=30°，AB=10。求BC，AC的长。解：由C=90°，A=30°，得BC= = 。由勾股定理得= = , ,= .即时练习：已知

10、在RtABC中，C=90°，A=45°，则BC=_，AC=_。DABC三、挖掘教材3、利用勾股定理求三角形的高例2 在. 分析：（1）图中有三个直角三角形，其中含CD的直角三角形都只有一条边长，不可以直接求CD的长；注意面积定理:由勾股定理可以求AB的长，从而求出CD。（2）在与中都缺少一个应用勾股定理的条件，可以设AD=，则BD=10，从两个不同的直角三角形用勾股定理表达出列出关于的方程，从而求CD。解:即时练习：，求（学生要画出草图）4、勾股定理在折叠中的应用例4 如图，已知长方形ABCD中AB=8 cm,BC=10 cm,在边CD上取一点E，将ADE折叠使点D恰好落在

11、BC边上的点F，求CE的长.分析：（在图中）标：AB= ，AD= ，（在图中）联：AF= ，BF= ，FC= 。设：CE= ，联：DE= ，EF= 。在中，由勾股定理列出方程求解:5、反思拓展：本节课数形结合与方程思想在勾股定理应用中得到了充分体现，希望同学们注意。【达标检测】1、在 中， ，若 ，则 2、三角形三个内角的比为1：2：3，它的最大边长为a，那么它的最小边是_3、 一轮船以16海里/小时的速度离A港向东北方向航行，另一艘轮船同时以12海里/小时的速度离A港向西北方向航行，2小时后，两船相距多少海里？（学生画出草图）4、在平静的湖面上，有一支红莲，高出水面1尺红莲被风一吹，花朵刚好

12、与水面平齐，已知红莲移动的水平距离是2尺问这里水深是多少？5、如图，受台风麦莎影响，一棵树在离地面4米处断裂，树的顶部落在离树跟底部3米处，这棵树折断前有多高？ 4米3米【学习课题】 第4课时 能得到直角三角形吗 【学习目标】1、了解勾股数的概念，熟悉常见的勾股数。2、掌握直角三角形的判别条件，正确区别勾股定理和判别条件的不同。3、运用判别条件解决简单问题，体会数学与现实生活的联系。【学习重点】判别三角形是直角三角形【学习难点】直角三角形判别条件的应用【候课朗读】 勾股定理【学习过程】学习准备：1、直角三角形中有 个角为直角，其中两个锐角是互为 ，两条直角边的 等于斜边的 。2、在RtABC中

13、，c=90 ,a:b=3:4，C=10，则a= ,b= 。活动探究(一)：每小组拿出直尺、圆规和量角器，分别以下列每组数为三边作三角形，相互交流并判断三角形的形状。（1）a=3cm， b=4cm， c=5cm， ， 是_三角形。（2）a=3cm， b=4cm， c=6cm， ， 是_三角形。（3）a=4cm， b=5cm， c=6cm， ， 是_三角形。（4）a=5cm， b=12cm， c=13cm， ， 是_三角形。解读教材： 1、从活动可知，边长分别是“3、4、5”和“5、12、13”的三角形一定是 三角形。2、如果三角形的三边长为a、b、c，满足，那么这个三角形一定是直角三角形，这是勾

14、股定理的逆定理。3、满足的三个正整数，称为 ，试写出三组勾股数 、 、 。即时练习1、下列各数是勾股数的是（ ）A、0.3、0.4、0.5 B、6、8、10 C、4、5、6 D、3/5、4/5、12、满足下列条件的ABC，不是直角三角形的是（ ）A、A=B-C B、A：B：C=1：1：2 C、a:b:c=1:1:2 D、b2=a2-c2 3、ABC中，如果AC2+BC2=AB2，那么 =90挖掘教材：例1 ：一个零件的形状如图，按规定这个零件中A 与BDC都应为直角，工人师傅量得零件各边尺寸：AD = 4，AB = 3, DC = 12 , BC=13，这个零件符合要求吗？ABCDABCD34

15、51213分析：要检验这个零件是否符合要求，只要判断ADB和DBC 是否为直角三角形，可使用勾股定理的逆定理。解：在ABD中， ABD为直角三角形， A =90°在BDC中，BDC是直角三角形，CDB =90°，因此这个零件符合要求。即时练习下列几组数能否作为直角三角形的三边长？说说你的理由9，12，15；15，36，39； 12，35，36；12，18，22已知ABC中BC=41, AC=40, AB=9, 则此三角形为_三角形, _是最大角. D C F A E B （图2）例2 ：如图2，在正方形ABCD中，E为AB中点，F为AD上一点，且，试判断EFC的形状，并说明理由即时练习1、三边长为n2-1、2n、n2+1（n>1）的三角形是不是直角三角形，为什么？2、如图（3）AD=24、BC=2