法拉第电磁感应定律

1、法拉第电磁感应定律法拉第电磁感应定律iE 4. 的计算的计算Ei （1）由）由B对称性可知对称性可知, 在同一圆周上在同一圆周上Ei的大小的大小 , 方向沿切线方向。方向沿切线方向。取半径为取半径为r 的电场线为积分路径，的电场线为积分路径，方向沿逆时针方向方向沿逆时针方向: :当当rR时时：dd2iBrEt d2iiLEl Er dBSt 例例5. 在半径为在半径为R的圆柱形区域有一均匀磁场的圆柱形区域有一均匀磁场B,且且 =C 0. 求求: （1）任意距中心）任意距中心o为为r处的处的Ei=?ddBtoabr 当当rRddd2BBSrtt dd22iBRErt 26RiEor0 iEd2i

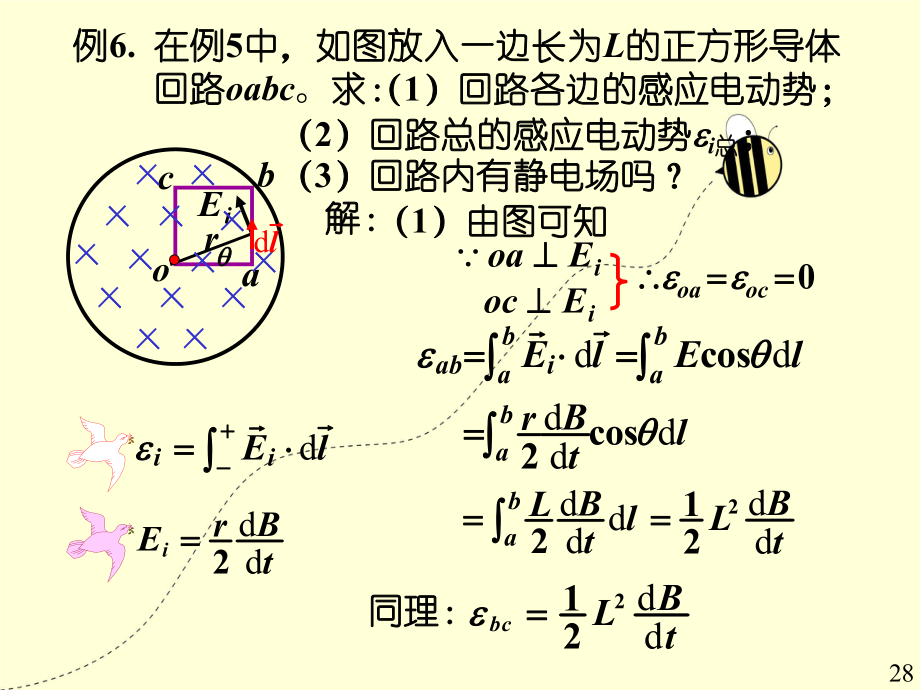
2、iLElEr ddiLSBElSt 2()r ddBt 2R iE例例6. 在例在例5中，如图放入一边长为中，如图放入一边长为L的正方形导体的正方形导体 回路回路oabc。求：求：（1）回路各边的感应电动势；）回路各边的感应电动势；解：解： （1）由图可知）由图可知iEoa iEoc 0 ocoa dbabiaEl dcosbaEl dddcos2baBrlt ddd2baBLlt dd212BLt 同理：同理：dd212bcBLt acbordiiEl dl dd2iBrEt 28 （2）回路总的感应电动势）回路总的感应电动势 i总总； （3）回路内有静电场吗？）回路内有静电场吗？解：解：或

3、或dd()B St ddBSt 29ddit iabbc dd2BLt iEacborl d （3）有静电场！）有静电场！oabc等效电路等效电路 ab= bc会使正电荷在会使正电荷在c点聚集，点聚集，而而a点有负电荷积累从而出现静电场点有负电荷积累从而出现静电场0 ocoa acVV 例例6.求求（2）回路总的感应电动势）回路总的感应电动势 i总总； （3）回路内有静电场吗？）回路内有静电场吗？ 若有若有, c与与a哪点电势高。哪点电势高。（2）总总总总abbc dd22BLt 例例7.在例在例5的磁场中，放有四根导体棒。的磁场中，放有四根导体棒。1）各导体棒中是否有感应电动势）各导体棒中是

4、否有感应电动势 i？ 若有，若有，比较其大小比较其大小。2）3，4连成通路连成通路 Ii=？3）棒中哪端电势高？）棒中哪端电势高？43 o12341）有）有2） Ii= 03）V右右 V左左解：解：312 01 对感应电场对感应电场 Ei补充说明：补充说明：iE 是涡旋场是涡旋场非保守场非保守场, 不能引入势函数，不能引入势函数，但它对在其场中的导体提供电动势：但它对在其场中的导体提供电动势：diiEl 导体不闭合时导体不闭合时使导体内电荷重新分布使导体内电荷重新分布产生产生EeieEEE静电平衡时：静电平衡时：ieEE eE 由于由于 的存在，则出现电势。的存在，则出现电势。则导体内的总电场

5、：则导体内的总电场：0 E 在导体内：在导体内：dd()ieLLElEEl 静电平衡时：静电平衡时：E = 0d()0ieLEEl 即：即：ddeiLLElEl iV V为导线两端电势差，即开路时电源的端电压。为导线两端电势差，即开路时电源的端电压。V 32i 0 （1）涡流）涡流5. 感应电场的应用感应电场的应用。将导体块放置在将导体块放置在Ei中中, 则在导体中将产生环形则在导体中将产生环形电流电流涡流。涡流。高频电磁感应炉高频电磁感应炉。但是涡流还是有害的，会消耗电功率，降低设但是涡流还是有害的，会消耗电功率，降低设备能量利用效率。备能量利用效率。33坩埚坩埚dd2iBrEt（2）物理学

6、中的应用）物理学中的应用电子感应加速器电子感应加速器问题：问题： 在电流在电流I的变化周期里的变化周期里,始终能给电子加速始终能给电子加速35原理原理:用变化磁场激发的感应电场来加速电子。用变化磁场激发的感应电场来加速电子。NS 交流电在前交流电在前1/4周期时周期时, ifmfiEvtI电子受力电子受力：iiEef （切向加速）（切向加速）Bvefm （提供向心力）（提供向心力）电子在管中沿逆时电子在管中沿逆时 针方向加速运动针方向加速运动. .ifmfiEv 管中管中的感应电场是顺时针的的感应电场是顺时针的(俯视图俯视图) 费曼认为，正确的物理学总是由这两个基本费曼认为，正确的物理学总是由

7、这两个基本定律给出：定律给出：FqEqvBBEt Lsl dBvsdtBdtd 212iBR 小结一下：小结一下：Lsl dBvsdtBdtd例例1.1.长直导线通有电流长直导线通有电流I I，在它附近放有一，在它附近放有一 矩形导体回矩形导体回路求路求若若I=kt，且回路又以，且回路又以v向右运动时，求向右运动时，求 i=？Ilab.ln2000vtavtbtkldtdi Lsl dBvsdtBvdlbktvdlaktdrlrkballba222000)(2)(2ln20000000vtbktlvvtaktlvvtavtbrkl四、互感与自感四、互感与自感1.1.互感互感L1L2（1）互感系

8、数）互感系数在在L2中产生感应电动势中产生感应电动势互感电动势互感电动势 1212反之反之: : L2中中i2的变化的变化,也在也在L1中产生互感电动势中产生互感电动势 2121L2中中 1212的变化的变化引起引起 显然显然 12、 21不仅与另一线圈的电流变化不仅与另一线圈的电流变化有关，而且还与它们的相对位置有关。有关，而且还与它们的相对位置有关。36L1中的中的i1变化变化 一导体回路的电流变化，在另一回路中一导体回路的电流变化，在另一回路中产生感应电动势产生感应电动势互感电动势。互感电动势。Mutaul inductance and self-inductance（电路中两种典型的电

9、磁感应）（电路中两种典型的电磁感应）设设L1的电流为的电流为i1, ,11Bi则则121B 121i 1212 1M i 同理同理: :2121 2M i L1L2M互感系数，简称互感。互感系数，简称互感。可证明：可证明：M12= M21=M单位单位: 亨利（亨利（H）两回路的位置有关两回路的位置有关;M与与线圈的几何形状及介质线圈的几何形状及介质 有关。有关。1i即有：即有：在在L2中产生的磁通匝链数为中产生的磁通匝链数为 1212。1i互感电动势：互感电动势：ddddddMiMMittt 当当 M = 常数时常数时ddMiMt dd221iMt dd112iMt 38（2）互感的计算）互感

10、的计算ddMiMt 112iM 221iM dddd121212122112MiiMitit 根据根据或或Mi 根据根据 物理意义：物理意义：单位电流的磁场在单位电流的磁场在另一线圈产生的磁通另一线圈产生的磁通r12解：由互感的定义可知解：由互感的定义可知211221Mii但此处但此处 21很难算出！很难算出！21201Mn ri 圆环中圆环中: 12 12 B B1 1 r2 = 0 ni1 r2 设此螺线管通有电流设此螺线管通有电流i1例例9. 长直螺线管，单位长度上有长直螺线管，单位长度上有n 匝线圈，另一匝线圈，另一 半径为半径为r 的圆环放在螺线管内，环平面与管的圆环放在螺线管内，环

11、平面与管 轴垂直。求它们之间的互感轴垂直。求它们之间的互感M？39则则 B1= 0 ni1例例10、一个横截面积为、一个横截面积为 S=1cm2，总匝数，总匝数N=10000匝匝的螺绕环上套着一个边长为的螺绕环上套着一个边长为 l=3cm的正方形单匝线圈，的正方形单匝线圈，环形螺线管的平均半径为环形螺线管的平均半径为R=10cm，今在正方形线圈中通，今在正方形线圈中通入一个强度为入一个强度为 I=at+I0 的电流，的电流，a=100 A/S，I0=2A，I 的的流向如图，试求环形螺线管的感生电动势的大小，并指流向如图，试求环形螺线管的感生电动势的大小，并指明明a、b两端哪端电势高？两端哪端电

12、势高？abR12解：设线圈解：设线圈2中通入电流中通入电流 i螺线管内部螺线管内部iRNniB 200线圈线圈1中中SB 21 螺绕环的截面螺绕环的截面SiRN 2021RNSiM 2021dtdIRNSdtdIM 2012247101021010000104 )(1024V b点电位高点电位高iI401 原则上可对任一线圈产生磁场计算另一原则上可对任一线圈产生磁场计算另一 线圈的磁通量线圈的磁通量 M = /i。2 互感在电工和无线电技术中应用广泛互感在电工和无线电技术中应用广泛 如如:变压器，互感器变压器，互感器互感往往也是有害的互感往往也是有害的但很多实际问题中但很多实际问题中M 很难算

13、出。很难算出。说明：说明：2.自感自感（1）自感电动势）自感电动势回路自身回路自身i变化变化B变化变化 变化变化B Li L自感系数或自感（电感）自感系数或自感（电感） 自自= Lddt ddddiLLitt 当当L=常量：常量：L L i 取决于回路的大小、取决于回路的大小、 形状、匝数以及形状、匝数以及 。iL ddLiLt i41 L的方向：反抗回路中电流的改变。的方向：反抗回路中电流的改变。电流增加时，自感电动势与原电流方向相反；电流增加时，自感电动势与原电流方向相反；电流减小时，自感电动势与原电流方向相同。电流减小时，自感电动势与原电流方向相同。 L总是阻碍回路总是阻碍回路自身电流的

14、变化自身电流的变化L iL 1ddLit ，回路里回路里 di/dt 0 L直流电路在直流电路在ON、off 开关的瞬间才出现开关的瞬间才出现 L。2LL L“电磁惯性电磁惯性”结论：结论：3 L的定义的定义:Li 42L大大, L大大阻碍电路变化的阻力大；阻碍电路变化的阻力大；L小小, L小小阻碍电路变化的阻力小。阻碍电路变化的阻力小。注意：两个定义式只有在注意：两个定义式只有在L是常量时是一致的是常量时是一致的L=常量常量ddddLiLLitt ddLiLt Li ddLitL 或或：例例11、求细长直螺线管的自感系数、求细长直螺线管的自感系数 （l、S、N） 假定螺线管通入电流假定螺线管

15、通入电流 I，因管中各处的，因管中各处的 B 是均匀的是均匀的NBSN lNISnISN200 真空中真空中体体VnlNSIL2020 介质中介质中r0“L”常数常数 说明：（说明：（1）铁磁质不能用上式计算）铁磁质不能用上式计算 （2）不仅线圈有自感，任何电路都有）不仅线圈有自感，任何电路都有 （2）自感）自感 L的计算的计算例例12. 两根平行输电导线，中心距离为两根平行输电导线，中心距离为d，半径为，半径为a， 求：两导线单位长度上的分布电感（求：两导线单位长度上的分布电感（da）。）。解：解： 如图，设导线中有电流如图，设导线中有电流I。单位长度上的磁通量：单位长度上的磁通量： sdB

16、 adaodrrI 2aadIo ln IL aado ln adoln ad dIIrdr adaodrrdI 2341i1N2N例例13、已知变压器、已知变压器 N1、N2、l、S、r求：求：L1、L2、M解：解：SlNLr 2101SlNLr 2202)(1212SBN SilNNr1210 112iM 2121LLkMLLM SinNr 1102不考虑漏磁，由不考虑漏磁，由 i1激发的磁通量全部穿进副线圈每一匝激发的磁通量全部穿进副线圈每一匝lr SSlNNr210 例例14、环形螺线管总匝数、环形螺线管总匝数 N （如图）（如图）（1）求）求 L= ？解解:设线圈中通入电流设线圈中通入电流 I hdrrNIsdBbas 20abhNIln20 IL （2）若中心一无限长直导线求）若中心一无限长直导线求M设直线中通电流设直线中通电流 I 1112IM （3）若在螺绕环中通以交变）若在螺绕环中通以交变 电流电流 ，求当，求当 时，在长直导线中时，在长直