全等三角形判定定理复习课件讲义.doc

1、全等三角形一、基本知识点知识点 1全等三角形的性质;全等三角形的对应边相等，全等三角形的对应角相等。知识点 2全等三角形的判定方法：一般三角形的判定方法：边角边（ SAS）、角边角（ ASA）、角角边（ AAS）、边边边（ SSS）直角三角形的判定方法：除了以上四种方法之外，还有斜边、直角边（ HL）知识点 3角平分线的性质：角的平分线上的点到角的两边的距离相等。符号语言： OP平分 MON（ 1 2）， PAOM， PB ON， PA PB知识点 4角平分线的判定方法：角的内部到角的两边的距离相等的点在角的平分线上。符号语言： PAOM， PBON， PAPB 1 2（ OP平分 MON）知

2、识点 5证明文字命题的一般步骤：证明文字命题， 第一是要根据题意画出合适的图形；第二要根据题意和图形写出已知和求证；第三是写出证明过程。二、本章应注意的问题1、全等三角形的证明过程：找已知条件，做标记；找隐藏条件，如对顶角、等腰三角形、平行四边形、公共边、公共角等；对照定理，看看还是否需要构造条件。2、全等三角形的证明思路：找夹角（ SAS）已知两边找直角（ HL ）找第三边（ SSS）若边为角的对边，则找任意角（ AAS）找已知角的另一边（SAS）已知一边一角边为角的邻边找已知边的对角（AAS）找夹已知边的另一角（ASA）找两角的夹边（ASA）已知两角找任意一边（AAS）13、全等三角形证明

3、中常见图形：B变形AEEDCGDEFAAD变形BCBC4、全等三角形证明时特殊的辅助线：在本章中，作辅助线的目的就是为了构造全等三角形，有几种特殊的辅助线需要注意：涉及三角形的中线问题时，常采用延长中线一倍的方法，构造出一对全等三角形；涉及角平分线问题时，经过角平分线上一点向两边作垂线，可以得到一对全等三角形；证明两条线段的和等于第三条线段时，用“截长补短”法可以构造一对全等三角形三、全等三角形习题精选1. 五大判定定理记忆与应用1下列命题中正确的是（）A全等三角形的高相等B全等三角形的中线相等C全等三角形的角平分线相等D全等三角形对应角的平分线相等2. 下列说法正确的是（）A. 周长相等的两

4、个三角形全等B.有两边和其中一边的对角对应相等的两个三角形全等C. 面积相等的两个三角形全等D.有两角和其中一角的对边对应相等的两个三角形全等3.如图 , 在 AOB 的两边上， AO=BO , 在 AO 和 BO 上截取 CO=DO , 连结 AD 和BC 交于点 P , 则 AOD BOC 理由是（）A.ASAB.SASC.AASD.SSS4. 如果两个三角形中两条边和其中一边上的高对应相等，那么这两个三角形的第三条边所对的角的关系是（）A.相等B.不相等C.互余或相等D.互补或相等2. 重点图形的识记1. 如图，已知 1=2， 3= 4， EC=AD，求证： AB=BE， BC=DB。D

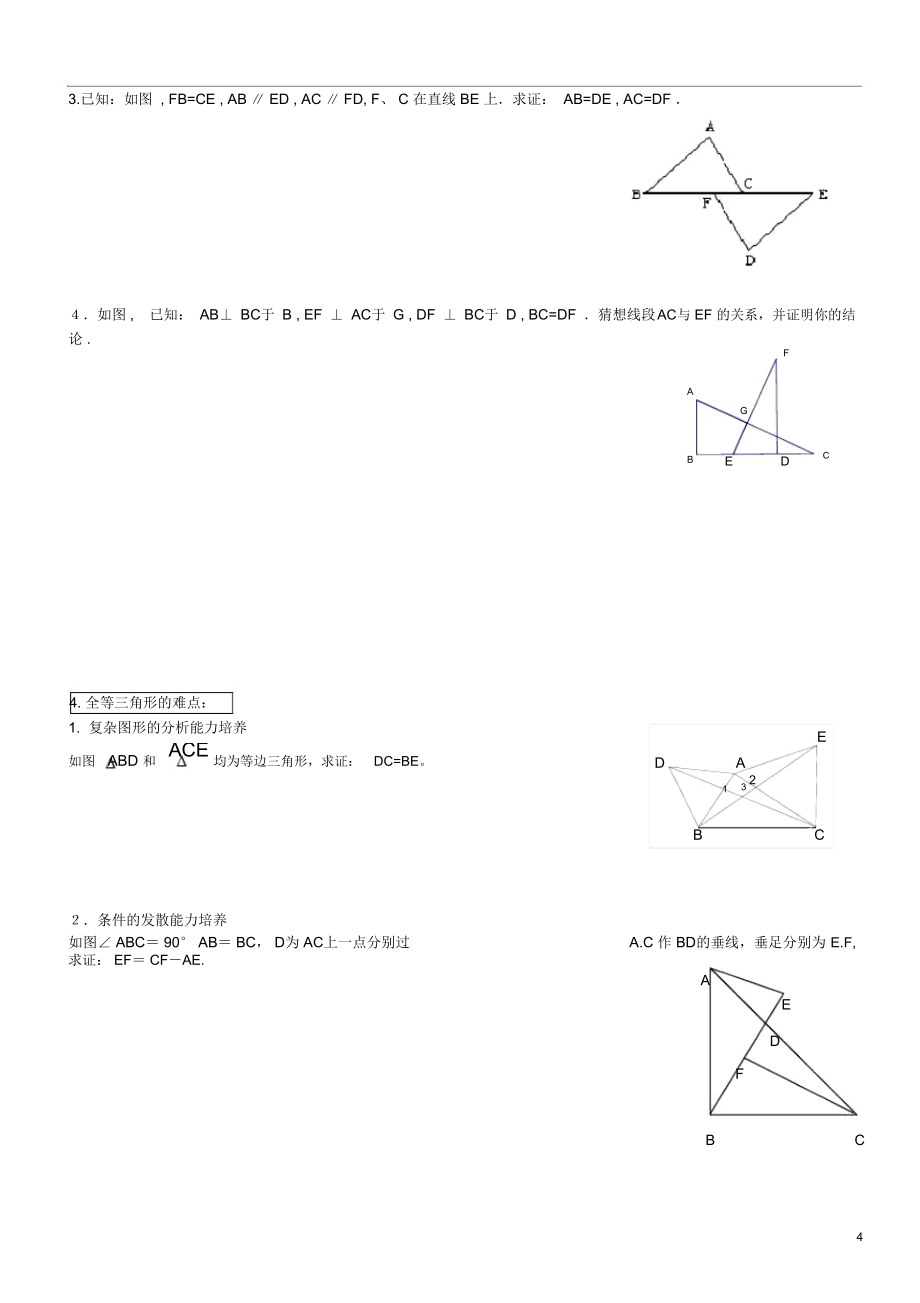
5、E3C42A1B22.如图， 1= 2， C= D， AC、 BD交于 E 点，求证： CE=DEDCEA12B3. 如图： AB=AC， EB=EC，AE的延长线交 BC于 D。求证： BD=DC。3. 重点证明过程的书写1. 如图， AE=AC， AD=AB， EAC= DAB，求证： ED CA2.如图，已知AB=AD， AC平分 DAB，求证：EBCEDC 。AEBDCECDABDACEB33.已知：如图 , FB=CE , AB ED , AC FD, F、 C 在直线 BE 上求证： AB=DE , AC=DF 如图 ,已知： AB BC于 B , EF AC于 G , DF BC

6、于 D , BC=DF 猜想线段AC与 EF 的关系，并证明你的结论 .FAGBEDC4. 全等三角形的难点：1. 复杂图形的分析能力培养E如图 ABD 和 ACE 均为等边三角形，求证： DC=BE。DA13 2BC条件的发散能力培养如图 ABC 90° AB BC， D为 AC上一点分别过A.C 作 BD的垂线，垂足分别为E.F, 求证： EF CFAE.AEDFBC45. 角平分线性质和判定的运用1、如图，在 ABC 中， C 90°，AD 是 BAC 的角平分线，若BC 5 ， BD 3 ，则点 D 到 AB 的距离为_2、如图， 在ABC 中，AD 为 BAC 的

7、平分线， DE AB 于 E，DF AC 于 F，ABC 面积是 28 cm2，AB=20cm ， AC=8cm ，则 DE 的长为 _ cm AEFBCD3、如图所示，在 ABC中， C90°， AC BC， AD 平分 CAB交 BC于 D， DE AB于 E， AB=10 求 BDE的周长4已知：如图，BD=CD ， CF AB 于点 F， BE AC 于点 E求证： AD 平分 BAC 6. 综合运用题1 ABC 中， ACB=90 °， AC=BC ，直线 MN 经过点 C，且 AD MN 于 D， BE MN 于 E(1) 当直线 MN 绕点 C 旋转到图的位置

8、时，求证：DE=AD+BE(2) 当直线 MN 绕点 C 旋转到图的位置时，求证：DE=AD-BE(3) 当直线 MN 绕点 C 旋转到图的位置时，试问：DE、 AD 、BE 有怎样的等量关系?请写出这个等量关系，并加以证明52如图 10，在四边形 ABCD 中， AD BC， E 为 CD 的中点，连结 AE 、BE，BE AE，延长 AE 交 BC 的延长线于点 F.求证：（ 1）FC =AD；（ 2）AB =BC+AD3已知点 E 是 BC 的中点，点 A 在 DE 上，且 BAE= CDE 猜想 AB 与 CD 数量关系，并说明理由 .DABEC64如图，四边形 ABCD 中， AB

9、DC，BE 、CE 分别平分 ABC 、 BCD ，且点 E 在 AD 上。求证： BC=AB+DC 。在四边形ABCD 中，BC>BA ，AD DC ，BD 平分ABC ，求证：AC180ADBC已知： AB=4 ，AC=2 ， D 是 BC 中点， AD 是整数，求ADABCD7赠送以下学习资料8和倍差倍问题学习目标通过和倍、差倍问题的学习，除了掌握这类问题的解决方法以外，其重点要学习画线段图。二、基础知识1. 和倍问题是已知两个数的和及它们之间的倍数关系而求这两个数各是多少的应用题。基本的数量关系： 和÷ ( 倍数 +1)= 较小数 ( 即 1 倍数、标准数 )2. 差倍

10、问题是已知两个数的差及它们之间的倍数关系而求这两个数各是多少的应用题。基本公式：差÷ ( 倍数的差 ) 标准数 ( 一倍数 )例题解析一、和倍问题例 1：某班为“希望工程”捐款，两组少先队员共交废报纸 240 千克，第一组交的废报纸是第二组的 3 倍，问两组各交废报纸多少千克？小结：解答基本的和倍问题，先确定其中一个数作为标准数(1 倍数 ) ，再找出两数的和，及其相对应的倍数关系，这样就可以求出标准数，也就可求出另一个数(较大数)。基本的数量关系： 和÷ ( 倍数 +1)=较小数 ( 即 1 倍数、标准数 )练一练：NBA球星姚明到底有多高？现在已知小明和姚明的身高和是3

11、39 厘米，姚明的身高大约是小明身高的2 倍。你能够算出来吗？例 2：哥哥原有 108 元，弟弟有 60 元，如果现在想把哥哥的钱调整到弟弟的 5 倍，弟弟应给哥哥多少钱？练一练： 妹妹有课外书 20 本，姐姐有课外书 25 本，姐姐给妹妹多少本后，妹妹课外书是姐姐的 2 倍？9例 3：二个同学共做了 23 道题。如果乙同学再多做 1 题，将是甲同学做的 2 倍，二个同学各做了几题？例 4：熊猫水果店运来水果 380 千克，其中苹果比梨的 3 倍还少 40 千克，水果店运来苹果和梨各多少千克 ?练一练：果园里种桃树和梨树共340 棵 , 其中桃树的棵数比梨树的3 倍多 20 棵，梨树种了多少棵

12、？例 5：三捆电线共长 273 米，其中第二根的长度是第一根长度的 2 倍，第三根的长度是第二根长度的 2 倍。三根电线各多少米？练一练： 甲、乙、丙三数的和是78，甲数比乙数的 2 倍多 4，乙数比丙数的 3 倍少 2。求这三个数。例 6：某小学有学生 975 人. 全校男生人数是六年级学生人数的 4 倍少 23 人，全校女生人数是六年级学生人数的 3 倍多 11 人. 问全校有男、女生各多少人？二、差倍问题例 1：某小学参观科普展览，第一天参观的人数比第二天多 200 人。已知第一天参观的人数是第二天的 3 倍，两天参观的各是多少人？练一练： 已知甲、乙两个数的商是4，而这两个数的差是30

13、，那么这两个数中较小的一个是多少？例 2：甲、乙两车间原来人数相等，因工作需要，从甲车间调 24 人到乙车间 . 这时乙车间人数是甲车间的 4 倍. 甲、乙两个车间原来各有多少人例 3：四（1）班与四（ 2）班原有图书的本数一样多。后来，四（ 1）班又买来新书 118 本，四（ 2）班从本班原有书中取出 70 本送给一年级同学。这时，四（ 1）班的图书是四（ 2）班的 3 倍。求两10班原有图书各多少本例 4：有大、小两猴都有一些桃子。小猴比大猴少 13 个，如果小猴再给大猴 6 个，这时小猴的桃子相当于大猴的 1 半，求大、小两猴原来各有多少个？练一练： 有两块布料，第一块 148 米，第二

14、块 100 米，两块布各剪去同样的一段后，剩下的米数第一块是第二块的 3 倍。两块布各剪去多长？例 5：猪、牛、羊跑步，如果，牛为猪跑得 2 倍，羊为牛跑的 4 倍，羊比猪多跑 56，那么三动物共跑了多少路？试一试： 两个自然数相除商是15，余数是 7，并且被除数比除数大735。求这两个数。例 6：某工厂有两堆煤，第一堆比第二堆多 50 吨，两堆煤各用去 75 吨后，剩下的第一堆煤是第二堆煤的 3 倍。求两堆煤原来各有多少吨？试一试： 用中国象棋的车，马，炮分别表示不同的自然数。如果：车÷马 2，炮÷车 4，炮马 56，那么“车马炮”等于多少？11课后作业 ：1. 小华和小瓜分别栽花和种瓜，一共 88 棵，小华栽花的棵数是小瓜种瓜棵数的 3 倍. 小华栽了多少花？小瓜种了多少瓜？2. 学校图书馆买来故事书、 科技书共 1000 本，科技书比故事书的 2 倍多 12 本，求学校买故事书、科技书各多少本 ?3. 果园里有梨树、桃树、核桃树共 526 棵。梨树比桃树的