



版权说明:本文档由用户提供并上传,收益归属内容提供方,若内容存在侵权,请进行举报或认领
文档简介
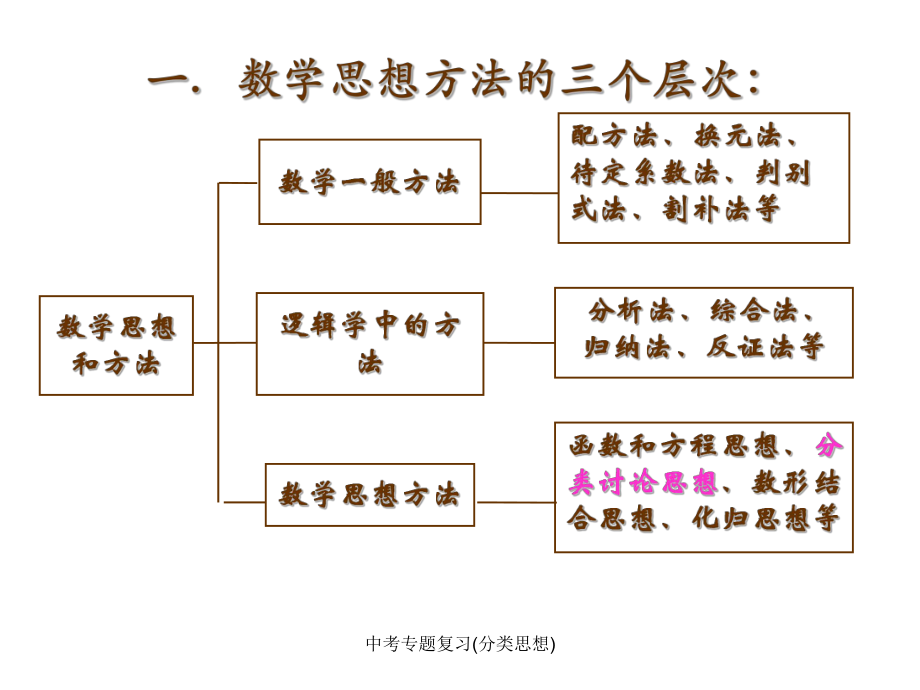
1、中考专题复习(分类思想)中考专题复习(分类思想)中考专题复习(分类思想)分类讨论思想分类讨论思想 分类思想是根据数学本质属性的相同点和不分类思想是根据数学本质属性的相同点和不同点,将数学研究对象分为不同种类的一种同点,将数学研究对象分为不同种类的一种数学思想。分类以比较为基础,比较是分类数学思想。分类以比较为基础,比较是分类的前提,分类是比较的结果。的前提,分类是比较的结果。 分类必须有一定的标准,标准不同分类的结分类必须有一定的标准,标准不同分类的结果也就不同。分类要做到不遗漏,不重复。果也就不同。分类要做到不遗漏,不重复。分类后,对每个类进行研究,使问题在各种分类后,对每个类进行研究,使问
2、题在各种不同的情况下,分别得到各种结论,这就是不同的情况下,分别得到各种结论,这就是讨论。讨论。中考专题复习(分类思想)分类讨论思想分类讨论思想 分类讨论是对问题深入研究的思想方法,用分类讨分类讨论是对问题深入研究的思想方法,用分类讨论的思想,有助于发现解题思路和掌握技能技巧,论的思想,有助于发现解题思路和掌握技能技巧,做到举一反三,触类旁通。做到举一反三,触类旁通。 分类的思想随处可见,既有概念的分类:如实数、分类的思想随处可见,既有概念的分类:如实数、有理数、绝对值、点(直线、圆)与圆的位置关系有理数、绝对值、点(直线、圆)与圆的位置关系和两圆相切等概念的分类;又有解题方法上的分类,和两圆
3、相切等概念的分类;又有解题方法上的分类,如代数式中含有字母系数的方程、不等式;还有几如代数式中含有字母系数的方程、不等式;还有几何中图形位置关系不确定的分类,等腰三角形的顶何中图形位置关系不确定的分类,等腰三角形的顶角顶点不确定、相似三角形的对应关系不确定等。角顶点不确定、相似三角形的对应关系不确定等。中考专题复习(分类思想)一一. .与概念有关的分类与概念有关的分类 1. 一次函数一次函数y=kx+b的自变量的取值范围是的自变量的取值范围是 -3x 6,相应的函数值的取值范围是,相应的函数值的取值范围是 -5y-2 ,则这个函数的解析式,则这个函数的解析式 。3131-5=-3k+b -2=
4、6k+b-5=6k+b-2=-3k+b解析式为解析式为 Y= x-4, 或或 y=- x-32. 函数函数y=ax2-ax+3x+1与与x轴只有一个交点,求轴只有一个交点,求a的值的值与交点坐标。与交点坐标。 当当a=0时时,为一次函数为一次函数y=3x+1,交点为(交点为(- ,0););当当a不为不为0时时,为二次函数为二次函数y=ax2+(3-a)x+1, =a2 -10a+9=0.解得解得a=1或或 a=9,交点为(交点为(-1,0)或()或( ,0)3131中考专题复习(分类思想)二二. .图形位置的分类图形位置的分类中考专题复习(分类思想)如图,线段如图,线段ODOD的一个端点的一
5、个端点O O在直线在直线a a上,以上,以ODOD为一边画等腰三角形,并且使另一个顶点在直线为一边画等腰三角形,并且使另一个顶点在直线a a上,这样的等腰三角形能画多少个上,这样的等腰三角形能画多少个? ?150a中考专题复习(分类思想) 在下图三角形的边上找出一点,使得该点与在下图三角形的边上找出一点,使得该点与三角形的两顶点构成三角形的两顶点构成等腰三角形等腰三角形!B BA AC C50501101102020中考专题复习(分类思想)1、对、对A进行讨论进行讨论2、对、对B进行讨论进行讨论3、对、对C进行讨论进行讨论CABACB20202020CAB5050CAB808020CAB656
6、550CAB3535110(分类讨论)(分类讨论)B BA AC C50501101102020中考专题复习(分类思想)3. 如图,直线如图,直线AB经过圆经过圆O的圆心,与圆的圆心,与圆O交于交于A、B两点,点两点,点C在在O上,且上,且AOC=300,点,点P是直线是直线AB上的一个动点(与点上的一个动点(与点O不重合),直线不重合),直线PC与圆与圆O相交于点相交于点Q,问点,问点P在直线在直线AB的什么的什么位置时,位置时,QP=QO?这样的点?这样的点P有几个?并相应地求出有几个?并相应地求出OCP的的度数。度数。ABCPOQ解:解:OQ=OC,OQ=QP OQC=OCQ,QOP=Q
7、PO 设设OCP=x0 , 则有:则有:(2)如果点)如果点P在线段在线段OB上,显然有上,显然有PQOQ,所以点,所以点P不可能在不可能在线段线段OB上。上。(1)如上图,)如上图, 当点当点P在线段在线段OA上时,上时, OQC=OCP=x, QPO= (1800OQP)= (1800 x)又又QPO=OCP+COP, (1800 x)=x+300, 解得解得x=400, 即即OCP=400212121中考专题复习(分类思想)OQCPBAQPOCBA(3)如图,当点在的延长线上时,)如图,当点在的延长线上时, OQC=OCQ=1800, OPQ= (1800 x)= x. 又又QCO=CP
8、O+COP,1800 x=x+300 解得解得x=1000 即即OCP=10002121(4)如图当在的延长线上时,)如图当在的延长线上时, OQC=OCQ=x,OQC=QPO+QOP, QPO= OQC= x, 又又COA=OCP+CPO, 解方程解方程30=x+ x, 得到得到x=200 即即OCP=200212121中考专题复习(分类思想)6。在。在ABC中,中,C=900,AC=3,BC=4。若以为圆。若以为圆心,为半径的圆与斜边只有一个公共点,则心,为半径的圆与斜边只有一个公共点,则R的值为多少?的值为多少?CBA4。在半径为。在半径为1的圆的圆O中,弦中,弦AB、AC的长的长分别是
9、分别是 、 ,则则BAC的度数是的度数是 。325。ABC是半径为是半径为2cm的圆的的圆的内接三角形,内接三角形,若若BC=2 cm,则角则角A的度数的度数是是 。3CABCACBBACCBACBA中考专题复习(分类思想)7.半径为半径为R的两个等圆外切,则半径为的两个等圆外切,则半径为2R且和这两个圆都相切且和这两个圆都相切的圆有几个?的圆有几个?中考专题复习(分类思想)8、在一张长为在一张长为9 9厘米,宽为厘米,宽为8 8厘米的矩形纸板上,剪下一个腰长厘米的矩形纸板上,剪下一个腰长为为5 5厘米的等腰三角形(要求等腰三角形的一个顶点与矩形的一厘米的等腰三角形(要求等腰三角形的一个顶点与
10、矩形的一个顶点重合,其余两个顶点在矩形的边上),请你计算剪下的个顶点重合,其余两个顶点在矩形的边上),请你计算剪下的等腰三角形的面积?等腰三角形的面积?中考专题复习(分类思想)22521AFAESAEF4352222BEEFBF1021BFAESAEF3452222DEEFDF21521DFAESAEF解:分三种情况计算:解:分三种情况计算:当当AE=AF=5AE=AF=5厘米时(图一)厘米时(图一)当当AE=EF=5AE=EF=5厘米时(图厘米时(图2 2)当当AE=EF=5AE=EF=5厘米时(图厘米时(图3 3) 中考专题复习(分类思想)三.与相似三角形有关的分类9。在矩形。在矩形ABC
11、D中,中,AB=12cm,BC=6cm,点,点P沿沿AB边从点边从点A出发向出发向B以以2cm秒的速度移动秒的速度移动;点点Q沿沿DA边从点边从点D开始向开始向A以以1cm/秒的速度移动。如果秒的速度移动。如果P、Q同时出发,用同时出发,用t秒表示移动的时间(秒表示移动的时间(0 x6)那么:)那么:(1)当)当t为何值时,为何值时,QAP为等腰直角三角形?为等腰直角三角形?(2)求四边形)求四边形QAPC的面积;的面积;提出一个与计算结果有关的结论;提出一个与计算结果有关的结论;(3)当)当t为何值时,以点为何值时,以点Q、A、P为顶点的三角形与为顶点的三角形与ABC相似?相似?QPADCB
12、中考专题复习(分类思想)解:对于任何时刻解:对于任何时刻t,AP=2t,DQ=t,QA=6,当,当=AP时,时,QAP为等腰直为等腰直 角三角形,即角三角形,即6t=2t,解得解得t=2(秒)(秒)(3)根据题意,可分为两种情况来研究)根据题意,可分为两种情况来研究在矩形在矩形ABCD中:中:当当 = 时,时,QAPABC,则,则 = ,解得解得t= =1.2秒。所以当秒。所以当t=1.2秒时,秒时,QAPABC。当当 = 时,时,PAQABC,则,则 = ,解得解得t=3(秒)。所以当(秒)。所以当t=3秒时,秒时,PAQABC。ABQABCAPBCQAABAP126 t62t5666 t1
13、22t(2)在)在QAC中,中,S= QADC= ( 6t)12=36在在APC中,中,S= APBC= QAPC的面积的面积S=(6t)+6t=36(cm2)由计算结果发现:在由计算结果发现:在P、Q两点移动的过程中,两点移动的过程中,四边形四边形QAPC的面积始终保持不变。的面积始终保持不变。21212121QPADCB中考专题复习(分类思想)10。已知二次函数。已知二次函数的图像与轴交于、两点的图像与轴交于、两点(点在点的左边),与轴交于点(点在点的左边),与轴交于点,直线(直线()与轴交于点。)与轴交于点。()求、三点的坐标;()求、三点的坐标;()在直线()在直线()上有一点(点在第
14、一象)上有一点(点在第一象限),使得以、为顶点的三角形与以、为顶限),使得以、为顶点的三角形与以、为顶点的三角形相似,求点的坐标。点的三角形相似,求点的坐标。中考专题复习(分类思想)解解(1)A(1,0),),B(1,0),),C(,(,2) 当当 PDB COB时,时, 有有P(m, 2m2););2m21(2) 当当 PDB BOC时,时, = 有(,)有(,)BOPDCOBDP中考专题复习(分类思想)CBCDC901612,BQP11. 如图所示,在直角梯形如图所示,在直角梯形ABCD中,中,AD/BC,AD=21。动点。动点P从点从点D出发,沿射线出发,沿射线DA的方向以每秒的方向以每
15、秒2个单位长个单位长的速度运动,动点的速度运动,动点Q从点从点C出发,在线段出发,在线段CB上以每秒上以每秒1个单位个单位长的速度向点长的速度向点B运动,点运动,点P,Q分别从点分别从点D,C同时出发,当点同时出发,当点Q运动到点运动到点B时,点时,点P随之停止运动。设运动的时间为(秒)。随之停止运动。设运动的时间为(秒)。(1)设)设BPQ的面积为的面积为S,求,求S与与t之间的函数关系式;之间的函数关系式;(2)当线段)当线段PQ与线段与线段AB相交于点相交于点O,且,且BO=2AO时,求时,求 (3)当)当t为何值时,以为何值时,以B、P、Q三点为顶点的三角形是等三点为顶点的三角形是等腰
16、三角形?腰三角形?的正切值;的正切值;(4)是否存在时刻是否存在时刻t,使得,使得PQBD?若存?若存在,求出在,求出 t的值;若不存在,请说明理由。的值;若不存在,请说明理由。中考专题复习(分类思想)PM BCPMDCQBtStt12161121216966()解:(解:(1)如图)如图1所示,过点所示,过点P作,作,垂足为垂足为M,则四边形,则四边形PDCM为矩形。为矩形。558,16)212( 216212ttttBQtAP,OAPOBQAPBQAOOB12(2)如图)如图2所示,由所示,由 得:得: 2930tan,293012tan,2BQPQPEBQPtPEQEQPEPEQRttPEtQCEDtPDEADQEQ中,在,垂足为作过点图图图图中考专题复习(分类思想)三角形是等腰三角形。三点为顶点的、秒时,以秒或当综合上面的讨论可知:不符合题意,舍去)解得,整理得:得:,由若。无实数根,
温馨提示
- 1. 本站所有资源如无特殊说明,都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
- 2. 本站的文档不包含任何第三方提供的附件图纸等,如果需要附件,请联系上传者。文件的所有权益归上传用户所有。
- 3. 本站RAR压缩包中若带图纸,网页内容里面会有图纸预览,若没有图纸预览就没有图纸。
- 4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
- 5. 人人文库网仅提供信息存储空间,仅对用户上传内容的表现方式做保护处理,对用户上传分享的文档内容本身不做任何修改或编辑,并不能对任何下载内容负责。
- 6. 下载文件中如有侵权或不适当内容,请与我们联系,我们立即纠正。
- 7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。
最新文档
- 环境监测仪器仪表的防爆设计与安全考核试卷
- 种子批发市场渠道融合与多元化发展考核试卷
- 2025年上海人力资源外包合同范本
- 2025写字间租赁合同书范本
- 乡村疾病控制策略试题及答案分析
- 2025机械设备购销合同范本
- 晶体光学慕课试题及答案
- 宋词导读考试题及答案
- 专利审查中的法律问题及其解决方法试题及答案
- 跨学科实践活动5 基于碳中和理念设计低碳行动方案(教学设计)九年级化学上册同步高效课堂(人教版2024)
- 铝合金模板细部节点深化设计指导图册(三维图)
- 2024年深圳技能大赛-鸿蒙移动应用开发(计算机程序设计员)职业技能竞赛初赛理论知识
- 毕业季营销活动方案
- QCT1182-2023汽车空调铝合金板式换热器
- 2024北京八十中初一(下)期中英语 (教师版)
- 海底泥石流预测与防治
- 年产2完整版本.5亿粒胶囊生产车间工艺的设计说明
- 2024届安徽省淮北市高三下学期二模英语模拟试题(有答案)
- 钢结构施工准备-钢结构识图
- 华为培训教程01网络基础
- 管道完整性管理基础知识课件

评论
0/150
提交评论