《应用回归分析》课后习题部分答案-何晓群版

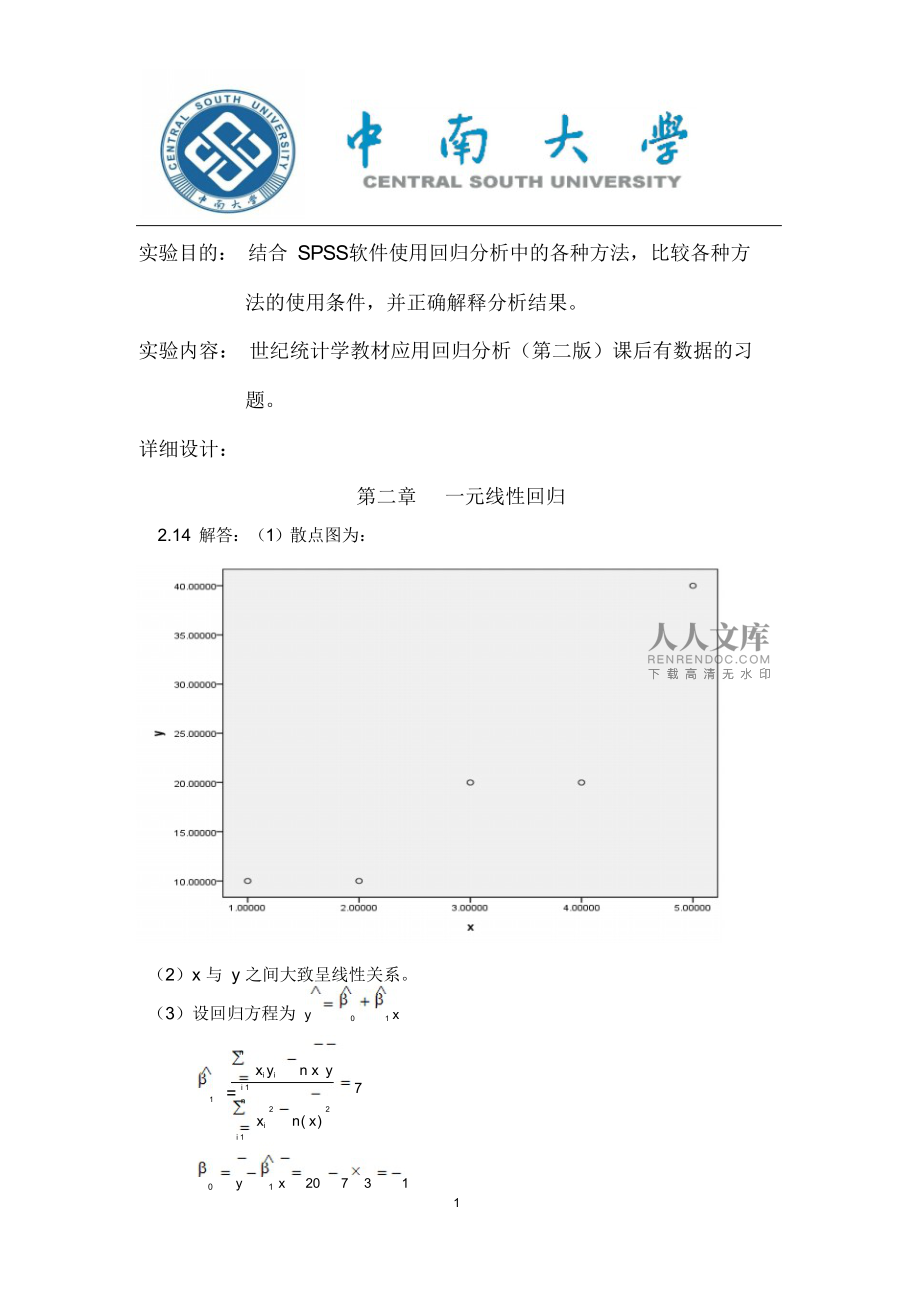
1、回归分析作业设计班级：统计 0802学号： 1303080513姓名：刘 贯 春 指导老师： 胡朝明日期： 2011 年 1 月 2 日实验目的： 结合 spss软件使用回归分析中的各种方法，比较各种方法的使用条件，并正确解释分析结果。实验内容： 世纪统计学教材应用回归分析（第二版）课后有数据的习题。详细设计：第二章一元线性回归2.14 解答：（1）散点图为：（2）x 与 y 之间大致呈线性关系。32（3）设回归方程为 y01 xn= i 1xi yin x y71n22xin( x)i 10y1 x20731可 得 回 归 方 程 为 y17 x2（4）1n-2ni=1( y i2yi )1

2、n-2ni=1( yi(012x )1 （ 10- （ -1+71） ）2=（ 10- （ -1+72 ） ）2（ 20- （ -1+73 ） ）23（ 20- （ -1+74） ）2 （ 40- （ -1+75 ） ）211 6904 93 631 1 0 / 313 3 06 . 13（5） 由于1n (1 ,2)l xxt112(1)lxx/ l xx服从自由度为 n-2 的 t 分布。因而(1)p|l xx|t / 2 (n2)1也即： p(1t / 211lxxt / 2l xx) =111可得 1 的 置 信 度 为 95% 的 置 信 区 间 为 （ 7-2.353即为：（ 2.

3、49 ，11.5）33 ， 7+2.3533333）21( x )20n (0 , ()nlxxt00002221( x)1( x) ()nl xxnlxx服从自由度为 n-2 的 t 分布。因而00p|21( x )nl xxt/ 2 ( n2)1221( x )1( x )即 p(0nlxxt / 200tnl xx/ 2 )1可得 1 的 置 信 度 为 95%的 置 信 区 间 为 （7.77, 5.77 ）（6） x 与 y 的决定系数 r 2n2( y iy )i 1n2( y iy)490 / 6000.817（7） （7）xi 1anov a平方和df均方f显著性组间（组合）9

4、.00024.5009.000.100线性项加权的8.16718.16716.333.056偏差.8331.8331.667.326组内1.0002.500总数10.0004由于 ff(1, 3),拒绝h 0 ,说明回归方程显著， x 与 y 有显著的线性关系。（8） t12/ l xx1lxx2n12其中ein2 i 11nn2 i 1( y i2y i )7131 02 13 . 6 633330t/ 22.353t3.66t/ 2接受原假设 h0 :10, 认为 1 显著不为 0，因变量 y 对自变量 x 的一元线性回归成立。n( xix )( yiy )（9）相关系数ri 1l xyn

5、nll( xix )2( y iy )xxyyi 1i 1=707600.90410600r 小于表中(10)序号1% 的相应值同时大于表中5% 的相应值，x 与 y 有显著的线性关系 .xyey111064221013-33320200442027-75残差图为：540346从图上看，残差是围绕e=0 随机波动，从而模型的基本假定是满足的。（11）当广告费x0 =4.2 万元时，销售收入y028.4 万 元 ，置 信 度 为 95% 的 置 信 区 间近 似 为 y2，即（ 17.1， 39.7）2.15 解答：（1） 散点图为：（2） x 与 y 之间大致呈线性关系。（3） 设回归方程为

6、y01 xnxi yin x y= i 1(2637021717)0.00361n22xin( x )i 1(71043005806440)0y1 x2.850.00367620.1068可 得 回 归 方 程 为 y0.10680.0036x(4)21n-2ni=1( yi2yi )1n-2ni=1( y i(012x)=0.23050.4801(5) 由 于 1n (1 ,2)l xxt11(12)lxx/ l xx服从自由度为 n-2 的 t 分布。因而(1)p|l xx|t / 2 (n2)1也即： p(1t / 211lxxt / 2l xx) =1可得 1 的 置 信 度 为 95

7、%的 置 信 区 间 为（ 0.0036-1.8600.4801/1297860， 0.0036+1.8600.4801/1297860）即为：（ 0.0028， 0.0044）21( x )20n (0 , ()nlxx0000t2221( x)1( x) ()nl xxnlxx服从自由度为 n-2 的 t 分布。因而00p|21( x )nl xxt/ 2 ( n2)1221( x )1( x )即 p(0nlxxt / 200tnl xx/ 2 )1可得 1 的 置 信 度 为 95%的 置 信 区 间 为 （0.3567,0.5703 ）2(6) x 与 y 的决定系数rn2( y i

8、y )i 1n2( y iy)16.8202718.525=0.908i 1(7) (7)xanov a平方和df均方f显著性组间（组合）1231497.5007175928.2145.302.168线性项加权的1168713.03611168713.03635.222.027偏差62784.464610464.077.315.885组内66362.500233181.250总数1297860.0009由于 ff(1, 9),拒绝h 0 ,说明回归方程显著， x 与 y 有显著的线性关系。(8) t12/ l xx1lxx2n12其中ein2 i 11n(n2 i 12yiy i )0 . 0

9、 0 3 61 2 9 7 8 6 08 . 5 4 20 . 0 4 8 0 1t/21.895t8.542t/ 2接受原假设h0 :10, 认为 1 显著不为 0，因变量 y 对自变量 x 的一元线性回归成立。nn(9) 相关系数rn( xii 1x )( yiy )l xy2l xx l yy( x ix )( yiy )i 1i 1=46530.9489129786018.525r 小于表中1% 的相应值同时大于表中5% 的相应值，x 与 y 有显著的线性关系 .(10) (10)序号xyey18253 53.07680.4232221510.88080.11923107043.958

10、80.0412455022.0868-0.0868548011.8348-0.8348692033.4188-0.4188713504.54.9688-0.466883251.51.27680.2232967032.51880.481210121554.48080.5192从图上看，残差是围绕e=0 随机波动，从而模型的基本假定是满足的。(11) 新 保 单 x 01000时 ， 需 要 加 班 的 时 间 为 y 03.7 小 时 。（ 12）y0的 置 信 概 率为 1-的 置 信 区 间 精 确 为 y 0t / 2 (n2)1h00,即为（ 2.7，4.7） 近似置信区间为：y 02，

11、即（ 2.74，4.66）（13） ）可得置信水平为 1-的 置 信 区 间 为 y 02.16 (1)散点图为：t / 2 ( n2)h00，即为（3.33，4.07）.可以用直线回归描述 y 与 x 之间的关系 .(2)回归方程为 : y(3)12112.6293.314 x从图上可看出，检验误差项服从正态分布。第三章 多元线性回归3.11 解：（1）用 spss算出 y，x1， x2,x3 相关系数矩阵：相关性yx1x2x3pearson 相关性y1.000.556.731.724x1.5561.000.113.398x2.731.1131.000.547x3.724.398.5471.

12、000y.048.008.009x1.048.378.127x2.008.378.051x3.009.127.051.ny10101010x110101010x210101010x310101010所以 r=模型非标准化系数标准系数系数ab 的 95.0%置信区间相关性共线性统计量b标准误差试用版tsig.下限上限零阶偏部分容差vif1( 常量)-348.2176.459-1.974.096-780.083.5008060x13.7541.933.3851.942.100-.9778.485.556.621.350.8251.211x27.1012.880.5352.465.049.05314

13、.149.731.709.444.6871.455x312.44710.569.2771.178.284-13.4138.310.724.433.212.5861.7085a. 因变量 : y(2)所以三元线性回归方程为y?348.283 .754 x17 .101 x 212 .447 x 3模型标准 估计的模型汇总更改统计量rr 方调整 r 方误差r 方更改f 更改df1df2sig. f更改1.898 a.806.70823.44188.8068.28336.015a. 预测变量 : ( 常量 ), x3, x1, x2。（3）由于决定系数 r方=0.708r=0.898较大所以认为拟合

14、度较高（4）anovab模型平方和df均方fsig.1回归13655.37034551.7908.283.015残差3297.1306549.522总计16952.5009aa. 预测变量 : (常量 ), x3, x1, x2。b. 因变量 : y因为 f=8.283p=0.0150.05所以认为回归方程在整体上拟合的好（5）模型非标准化系数标准系数系数ab 的 95.0%置信区间相关性共线性统计量b标准误差试用版tsig.下限上限零阶偏部分容差vif1(-348.280176.459-1.974.096-780.06083.500常量)x13.7541.933.3851.942.100-.

15、9778.485.556.621.350.8251.211x27.1012.880.5352.465.049.05314.149.731.709.444.6871.455x312.44710.569.2771.178.284-13.41538.310.724.433.212.5861.708a.因变量 : y（6） ）可以看到 p 值最大的是 x3 为 0.284 ，所以 x3 的回归系数没有通过显著检验，应去除。去除 x3 后作 f 检验，得：anovab模型平方和df均方fsig.1回归12893.19926446.60011.117.007 a残差4059.3017579.900总计16

16、952.5009a. 预测变量 : (常量 ), x2, x1。b. 因变量 : y由表知通过 f 检验继续做回归系数检验模型非标准化系数b标准 误差标准系数试用版系数tasig.b 的 95.0%下限置信区间上限相关性零阶偏部分共线性统计量容差vif1( 常量 )-459.624153.058-3.003.020-821.547-97.700x14.6761.816.4792.575.037.3818.970.556.697.476.9871.013x28.9712.468.6763.634.0083.13414.808.731.808.672.9871.013a.因变量: y此时，我们发现

17、 x1，x2 的显著性大大提高。（ 7） x1:(-0.997,8.485)x2:(0.053,14.149)x3:(-13.415,38.310)(8) y?*(9)*0 .385 x1*0 .535 x 2*0 .277 x 3极小值a残差统计量极大值均值标准 偏差n预测值175.4748292.5545231.500038.9520610标准 预测值-1.4381.567.0001.00010预测值的标准误差10.46620.19114.5263.12710调整的预测值188.3515318.1067240.183549.8391410残差-25.1975933.22549.000001

18、9.1402210标准 残差-1.0751.417.000.81610student化 残差-2.1161.754-.1231.18810已删除的残差-97.6152350.88274-8.6834843.4322010student化 已删除的残差-3.8322.294-.2551.65810mahal。 距离.8945.7772.7001.55510cook 的距离.0003.216.486.97610居中杠杆值.099.642.300.17310a.因变量 : y所以置信区间为（ 175.4748 ，292.5545 ）（ 10）由于 x3 的回归系数显著性检验未通过，所以居民非商品支出

19、对货运总量影响不大，但是回归方程整体对数据拟合较好3.12 解：在固定第二产业增加值，考虑第三产业增加值影响的情况下，第一产业每增加一个单位， gdp就增加 0.607 个单位。在固定第一产业增加值，考虑第三产业增加值影响的情况下，第二产业每增加一个单位， gdp就增加 1.709 个单位。4.9解：第四章 违背基本假设的情况a系数模型非标准化系数标准系数b标准误差试用版tsig.1( 常量)-.831.442-1.882.065x.004.000.83911.030.000a.因变量 : y由 spss计算得： y? =-0.831+0.004x残差散点图为：（2） ）由残差散点图可知存在异

20、方差性再用等级相关系数分析：相关系数xt*spearman 的 rhox相关系数1.000.318sig.（双侧）.021n5353t相关系数.318 *1.000sig. （双侧）.021.n5353*.在置信度（双测）为0.05时，相关性是显著的。p=0.021 所以方差与自变量的相关性是显著的。（ 3）模型描述因变量y自变量1x权重源x幂值1.500模型: mod_1.m=1.5 时可以建立最优权函数，此时得到：anova平方和df均方fsig.回归.0061.00698.604.000残差.00351.000总计.00952系数未标准化系数标准化系数b标准误试用版标准误tsig.（常数

21、）-.683.298-2.296.026系数未标准化系数b标准误标准化系数试用版标准误tsig.（常数）-.683.298-2.296.026x.004.000.812.0829.930.000所以： y?-0.683+0.004x（ 4）a系数模型非标准化系数标准系数b标准误差试用版tsig.1( 常量).582.1304.481.000xa.因变量 : yy.001.000.8059.699.000模型rr方调整 r 方标准估计的误差durbin-watson1.999 a.998.998.09744.6634.13解：(1)系数a模型非标准化系数标准系数b标准 误差试用版tsig.1(

22、常量)-1.435.242-5.930.000x.176.002.999107.928.000a.因变量 : yy? =-1.435+0.176x(2)模型汇总ba. 预测变量 : (常量 ), x 。b. 因变量 : ydw=0.663 查 dw分布表知： d l =0.95所以 dwd l残差图为：, 故误差项存在正相关。et 随 t 的变化逐次变化并不频繁的改变符号，说明误差项存在正相关。（ 3） ? =1-0.5*dw=0.6685 计算得：yx7.3944.907.6545.806.8440.698.0048.507.7946.858.2649.457.9648.478.2850.0

23、47.9048.038.4951.177.8847.268.7752.338.9352.699.3254.959.2955.549.4856.779.3855.839.6758.009.9059.22模型汇总模型rr 方调整 r 方b标准 估计的误差durbin-watsona1.996.993.993.073951.344a. 预测变量 : (常量 ), xx。b. 因变量 : yy模型非标准化系数b标准a系数误差标准系数试用版tsig.1( 常量)-.303.180-1.684.110xx.173.004.99649.011.000a.因变量 : yy得回归方程 y? =-0.303+0.

24、173x即： y?t =-0.303+0.6685 y t 1 +0.173（ x t 0.6685 x t 1 ）（ 4）b模型汇总模型rr方调整 r 方标准估计的误差durbin-watson1.978 a.957.955.074491.480a. 预测变量 : (常量 ), x3。b. 因变量 : y3a系数模型非标准化系数标准系数b标 准 误差试用版tsig.1( 常量).033.0261.273.220x3.161.008.97819.528.000a. 因变量 : y31( 常量)-574.062349.271-1.644.107x1191.09873.309.3452.607.0

25、12x22.045.911.2972.246.029 y t =0.033+0.161 x t即： y?t =0.033+ y t 1 +0.161 （ x t - x t 1 ）（ 5）差分法的 dw值最大为 1.48 消除相关性最彻底，但是迭代法的0.07395 ，拟合的较好。? 值最小为4.14 解：（ 1）模型汇总b模型标准rr 方调整 r 方估计的误差durbin-watson1.541a.293.264329.69302.745a.b.预测变量 : (常量 ), x2, x1因变量 : y。系数a模型非标准化系数标准系数b标准 误差试用版tsig.a.因变量 : y回归方程为： y

26、? =-574.062+191.098x1+2.045x2dw=0.745dl 所以误差项存在正相关残差图为：（ 2） ? =1-0.5*dw=0.6275模型汇总模型rr 方调整 r 方b标准 估计的误差durbin-watsona1.688.474.452257.670641.716a. 预测变量 : (常量 ), x22, x12。b. 因变量 : y2a系数模型非标准化系数标准系数b标准误差试用版tsig.1( 常量)-179.66890.337-1.989.052x12211.77047.778.5224.432.000x22a.因变量 : y21.434.628.2692.283.

27、027此时得方程： y?t =-179.668+211.77x1 +1.434x2 所以回归方程为：y?t179.6680 .6275y t 1211.77 ( x1t0 .6275x1t1? )1 .434( x 2 t0 .6275x 2 t 1 )（3） ）模型汇总模型rr 方调整 r 方b标准 估计的误差durbin-watsona1.715.511.490283.791022.042a. 预测变量 : (常量 ), x23, x13。b. 因变量 : y3a系数模型非标准化系数标准系数b标准误差试用版tsig.1( 常量)7.69839.754.194.847x13209.89144

28、.143.5444.755.000x231.399.583.2742.400.020a.因变量 : y3)此时得方程：y?t7 .698209.891x11.399x 2所以回归方程为：y?t7. 698209.891 ( x tx t 11 .399( x 2 tx 2 t 15.9 后退法：输出结果第五章 自变量选择与逐步回归系数 a模型非标准化系数标准系数b标 准 误差试用版tsig.1(常量)1438.1202252.472.638.533农业 x1-.626.168-1.098-3.720.002工业 x2-.328.207-1.352-1.587.135建筑业 x3-.383.55

29、5-.251-.691.501人口 x4-.004.025-.014-.161.875最终消费x5.672.1303.7105.178.000受灾面积x6-.006.008-.015-.695.4992(常量)1079.754299.7593.602.003农业 x1-.642.130-1.126-4.925.000工业 x2-.303.131-1.249-2.314.035建筑业 x3-.402.525-.263-.765.456最终消费x5.658.0953.6366.905.000受灾面积x6-.006.007-.017-.849.4093(常量)1083.150295.8163.662

30、.002农业 x1-.624.127-1.095-4.931.000工业 x2-.373.093-1.535-3.998.001最终消费x5.657.0943.6276.981.000受灾面积 x6-.005.007-.015-.758.4604(常量)874.604106.8698.184.000农业 x1-.611.124-1.073-4.936.000工业 x2-.353.088-1.454-3.994.001最终消费x5.637.0893.5167.142.000a. 因变量 : 财政收入 yanovae模型平方和df均方fsig.1回归1.365e862.274e7602.127a.

31、000残差528793.3191437770.951总计1.370e8202回归1.365e852.729e7772.734.000b残差529767.8521535317.857总计1.370e8203回归1.364e843.411e7991.468.000c残差550440.1031634402.506总计1.370e8204回归1.364e834.547e71355.753d.000残差570180.9311733540.055总计1.370e820a. 预测变量 : (常量), 受灾面积 x6, 建筑业 x3, 人口 x4, 农业 x1, 最终消费 x5, 工业 x2。b. 预测变量

32、: (常量 ), 受灾面积 x6, 建筑业 x3, 农业 x1, 最终消费 x5, 工业 x2。c. 预测变量 : (常量), 受灾面积 x6, 农业 x1, 最终消费 x5, 工业 x2。d. 预测变量 : (常量 ), 农业 x1, 最终消费 x5, 工业 x2。e. 因变量 : 财政收入 y模型汇总模型更改统计量rr方调整r方标准估计的误差r方更改f 更改df1df2sig. f 更改1.998a.996.994194.34750.996602.127614.0002.998b.996.995187.93046.000.026114.8753.998c.996.995185.47913.

33、000.585115.4564.998d.996.995183.13944.000.574116.460a. 预测变量 : (常量 ), 受灾面积 x6, 建筑业 x3, 人口 x4, 农业 x1, 最终消费 x5, 工业 x2。b. 预测变量 : (常量 ), 受灾面积 x6, 建筑业 x3, 农业 x1, 最终消费 x5, 工业 x2。c. 预测变量 : (常量 ), 受灾面积 x6, 农业 x1, 最终消费 x5, 工业 x2。d. 预测变量 : (常量 ), 农业 x1, 最终消费 x5, 工业 x2。回归方程为： y874.6040.611 x10.353 x20.637 x5逐步回

34、归法：输出结果模型汇总模型更改统计量rr方调整r方标准估计的误差r方更改f 更改df1df2sig. f更改1.994a.989.988285.68373.9891659.441119.0002.996b.992.991247.77768.0037.258118.0153.998c.996.995183.13944.00415.948117.001a. 预测变量 : (常量 ), 最终消费 x5。b. 预测变量 : (常量 ), 最终消费 x5, 农业 x1。c. 预测变量 : (常量 ), 最终消费 x5, 农业 x1, 工业 x2。anovad模型平方和df均方fsig.1回归1.354e

35、811.354e81659.441.000a残差1550688.6541981615.192总计1.370e8202回归1.359e826.794e71106.637.000b残差1105088.0031861393.778总计1.370e8203回归1.364e834.547e71355.753.000c残差570180.9311733540.055总计1.370e820a. 预测变量 : (常量), 最终消费 x5。b. 预测变量 : (常量 ), 最终消费 x5, 农业 x1。c. 预测变量 : (常量), 最终消费 x5, 农业 x1, 工业 x2。d. 因变量 : 财政收入 y模型非标准化系数标准系数系数 a相关性710.37290.8917.816.000.180.004.99440.736.000.994.994.9941011.