圆弧计算公式及运用

1、圆弧计算公式及运用.教学内容：弧长及扇形的面积 圆锥的侧面积二.教学要求1、了解弧长计算公式及扇形面积计算公式，并会运用公式解决具体问题。2、了解圆锥的侧面积公式，并会应用公式解决问题。三.重点及难点 重点：1、弧长的公式、扇形面积公式及其应用。2、圆锥的侧面积展开图及圆锥的侧面积、全面积的计算。 难点：1、弧长公式、扇形面积公式的推导。2、圆锥的侧面积、全面积的计算。知识要点知识点1、弧长公式的圆心角所对的弧长是1 _ 讥艮I的计算公式：面，180都不带单位“度”，因为360的圆心角所对的弧长就是圆周长C= 2疔R,所以12kR 即 7R面，于是可得半径为R的圆中，n的圆心角所对的弧长 说明

2、：(1)在弧长公式中，n表示1的圆心角的倍数，n和x3OxLOjt例如，圆的半径R= 10,计算20的圆心角所对的弧长I时，不要错写成1舱。(2)在弧长公式中，已知I, n, R中的任意两个量，都可以求出第三个量。R，圆心角为n 的扇形面积，360。的扇形面积等于圆面积显然扇形的面积 帧，所以圆心角知识点2、扇形的面积如图所示，阴影部分的面积就是半径为 是它所在圆的面积的一部分，因为圆心角是为1 的扇形面积是凭0，由此得圆心角为* nfrR1甸，扇形面积又因为扇形的弧长n的扇形面积的计算公式是可以写顺-/?玄D2 1甜，所以又得到扇形面积的另一个计算公式：蘭甩rJ知识点3、弓形的面积(1) 弓

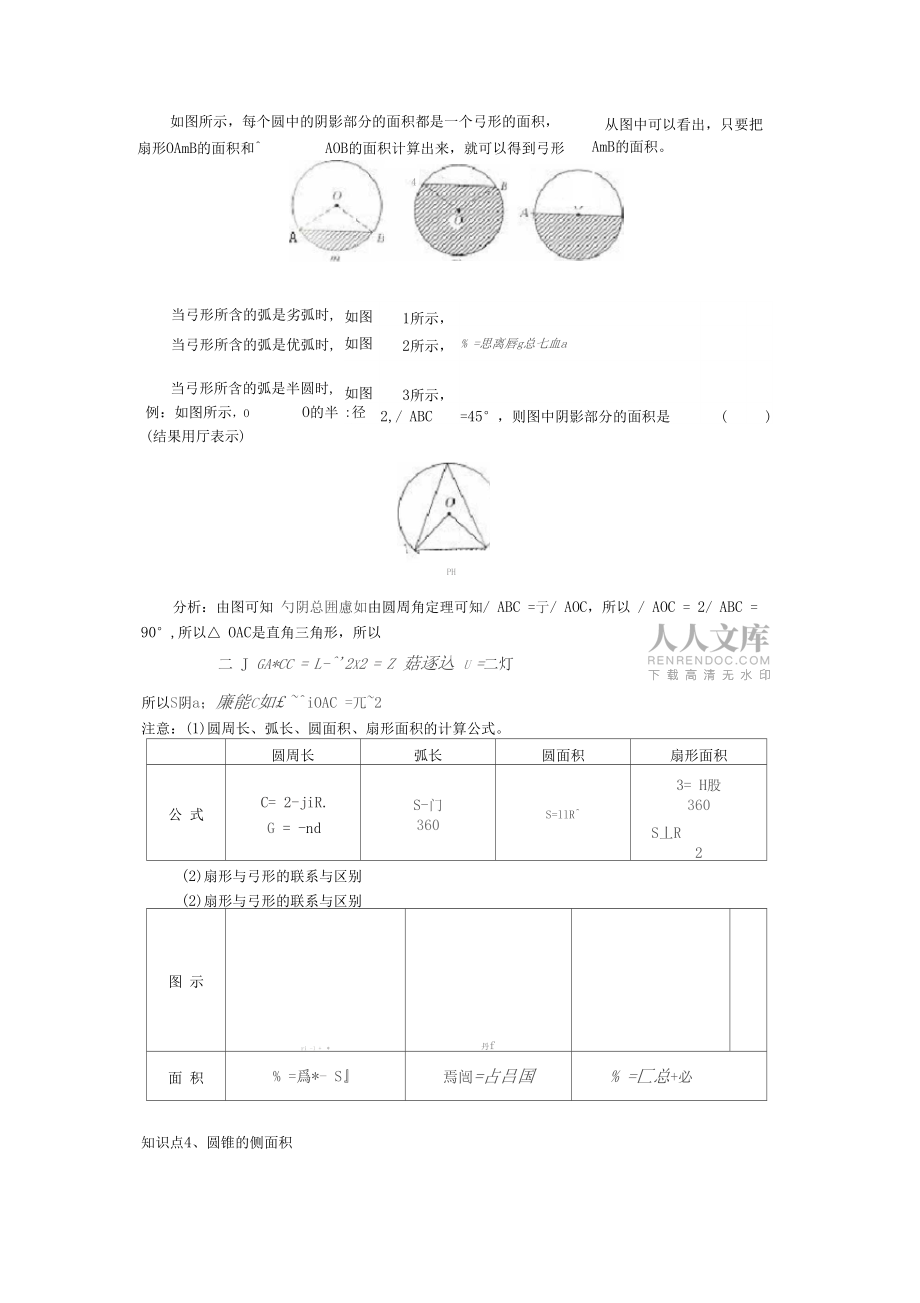
3、形的定义：由弦及其所对的弧(包括劣弧、优弧、半圆)组成的图形叫做弓形。(2) 弓形的周长=弦长+弧长(3) 弓形的面积从图中可以看出，只要把 AmB的面积。4fl当弓形所含的弧是半圆时, 例：如图所示，O O的半 (结果用厅表示)如图1所示，如图2所示，% =思离唇g总七血a如图3所示，:径为2,/ ABC=45，则图中阴影部分的面积是()当弓形所含的弧是劣弧时,当弓形所含的弧是优弧时,PH如图所示，每个圆中的阴影部分的面积都是一个弓形的面积，扇形OAmB的面积和AOB的面积计算出来，就可以得到弓形分析：由图可知 勺阴总囲慮如由圆周角定理可知/ ABC =亍/ AOC，所以 / AOC = 2

4、/ ABC = 90,所以 OAC是直角三角形，所以二 J GA*CC = L-2x2 = Z 菇逐込 u =二灯所以S阴a；廉能C如 iOAC =兀2注意：(1)圆周长、弧长、圆面积、扇形面积的计算公式。圆周长弧长圆面积扇形面积公 式C= 2-jiR.G = -ndS-门360S=llR3= H股360S丄R2(2)扇形与弓形的联系与区别(2)扇形与弓形的联系与区别图 示ri -1 +*丹f面 积% =爲*- S焉闿=占吕国% =匚总+必知识点4、圆锥的侧面积I，底面圆的半径为r,圆锥的侧面展开图是一个扇形，如图所示，设圆锥的母线长为 那么这个扇形的半径为I，扇形的弧长为2珊，圆锥的侧面积细

5、亦，圆锥的全面积E仝三呂鶴* E底卅i +册+说明：（1）圆锥的侧面积与底面积之和称为圆锥的全面积。（2）研究有关圆锥的侧面积和全面积的计算问题，关键是理解圆锥的侧面积公式，并 明确圆锥全面积与侧面积之间的关系。知识点5、圆柱的侧面积知识小结：圆锥与圆柱的比较名称图形图形的形成过程图形的组成 侧面展开图的特征面积计算方法圆锥|_匸_由一个直角三角形旋转得到 的，女0 Rt SOA绕直线 SO 旋转一周。一个底面和一个侧面扇形弘皿1呂仝呂 + S慝-冗ri+町之圆柱由一个矩形旋转得到的，如矩形 ABCD绕直线AB旋转一周。两个底面和一个侧面矩形Spg - 2jcrhS徨 购 + 2S慝-2：5i

6、ih + 210之圆柱的侧面积展开图是矩形， 如图所示，其两邻边分别为圆柱的高和圆柱底面圆的周长， 若圆柱的底面半径为r ,高为h ,则圆柱的侧面积召-2於,圆柱的全面积 E隹=S韵+S庭=為从亦=3疔（时+ F）【典型例题】2, 1,/ AOB = 120例1.（2003.辽宁）如图所示，在同心圆中，两圆的半径分别为则阴影部分的面积是（）471A. 4兀 B.加 C. 3D. n分析：阴影部分所在的两个扇形的圆心角为360-ZAOa =360-120= 240所以务達.思I-%光D故答案为：B.liZ40 亠 240,H X 1例2.（2004 陕西）如图所示，点3厘米，tan/ BAC =

7、 4 ,求阴影部分的面积。C在以AB为直径的半圆上，连接 AC, BC, AB = 10分析：本题考查的知识点有： 识（3）组合图形面积的计算。解：因为AB为直径，所以/（1）直径所对圆周角为在 Rt ABC 中，AB = 10,设BC = 3k, AC = 4k,（ k不为0,且为正数）由勾股定理得加+叫所以k = 290,（ 2）解直角三角形的知ACB = 90,3tan/ BAC = 4 ,而 tan/ BAC =丿亡SC= 24 所以 BC = 6, AC = 8,225_ 2 皿=25=7C2所以例3.（2003.福州）形 AOB ,点 C, E, D垂足为F,如果正方形的边长为 1

8、，那么阴影部分的面积为（Ji的圆心角为直角，正方形 OCDE内接于扇如图所示，已知扇形 AOB分别在OA , OB及AB弧上，过点A作AF丄ED交ED的延长线于 F, ）1，所以OE = DE = 1,所以00 =的，设两部分阴影的面积中的N，则皿=用矗屈总他-心。皿阳=帝能迹5-忙|和加助1，阴影部分面用割补法解此题较为简单，设一部分空白面积为P,因为正方形的边长为分析：连接 OD，由正方形性质可知/ EOD = / DOC = 45,在 Rt OED中，OD =一部分为M ,另一部分为 积可求，但这种方法较麻烦，因为/ BOD =/ DOC，所以名丽BOD = Jjyi5D0A* 所以耐

9、* 九ED =卩*所以弘ED = iOCE-正 H庁 mde - 0A - 0E -亠h - 1所以M = P,所以答案：应-1。例 4.如图所示，直角梯形 ABCD 中，/ B = 90, AD / BC , AB = 2, BC = 7, AD = 3, 以BC为轴把直角梯形 ABCD分析：将直角梯形ABCD绕BC旋转一周所得的几何体是由相同底面的圆柱和圆锥组 成的，所得几何体的表面积是圆锥的侧面积、圆柱的侧面积和底面积三者之和。解：作DH丄BC于H，所以DH = AB = 2CH = BC BH = BC AD = 7 3 = 4在 CDH中，CD = JdL + CH： = 仃 4?

10、= 275所以S克=S型氓g + S因庄貼+恿=1DHCD + AB AD + (AB) = 4运+ 16ii例5. (2003.宁波)已知扇形的圆心角为120，面积为30W平方厘米(1) 求扇形的弧长。R,扇形的弧长可由弧长(2) 若把此扇形卷成一个圆锥，则这个圆锥的轴截面面积是多少？S分析：(1)由扇形面积公式S =公式 360求得。(2)由此扇形卷成的圆锥如图所示，这个圆锥的轴截面为等腰三角形ABC , ( 1)问中求得的弧长是这个圆锥的底面圆周长，而圆周长公式为C = 2疔r,底面圆半径r即CD的长可求，圆锥的高AD可在Rt ADC中求得，所以叽也厂2直。*巳匚可求。 解：(1)设扇形

11、的半径为 R,30011 = ，得药0，解得R= 30.jtR. =xzo = aojT所以扇形的弧长（2）如图所示,ISO ISO（厘米）。在等腰三角形 ABC中，AB = AC = R = 30, BC = 2r，底面圆周长 C =2r,因为底面圆周长即为扇形的弧长，所以2加=20%所加=10在Rt ADC中，高AD =伍匸莎=莎二而=如忑瓦 =J-AD* BC = ix2DV3 x20 = 200 Ji所以轴截面面积22（平方厘米）。【模拟试题】（答题时间：40分钟）、选择题A. 4 B. 2 庞2.扇形的圆心角是1. 若一个扇形的圆心角是 45,面积为2沢，则这个扇形的半径是（ C.

12、47 JID. 2 罷 JI60,则扇形的面积是所在图面积的（A. M B. 63. 扇形的面积等于其半径的平方，则扇形的圆心角是（1册A. 90 B.汇4. 两同心圆的圆心是 径是小圆半径的3倍,A. 2倍 B. 3倍5. 半圆0的直径为A QM-g屈品(37r C. 2C.兀 D.180 0,大圆的半径是以 0A，0B分别交小圆于点 则扇形0AB的面积是扇形 0MN的面积的（C. 6倍 D. 9倍6cm, / BAC = 30，则阴影部分的面积是（孑JT- ?书）炖2B. 4N .已知大圆半7.D.用一个半径长为 6cmA. 2 cmB. 3cm圆锥的全面积和侧面积之比是A.30 B. 6

13、0 的半圆围成一个圆锥的侧面，则此圆锥的底面半径为C. 4cmD. 6cm3 : 2，这个圆锥的轴截面的顶角是（C.90 D.120 已知两个母线相等的圆锥的侧面展开图恰好能拼成一个圆, 2,则它们的高之比为（且它们的侧面积之比为 1 :A. 2 : 1 B. 3 : 29.如图，在 ABC中， 的侧面积为Si，以BC为底面圆半径,）C. 2罷:的 D. 5 : 2屈/ C = Rt/, AC BC，若以AC为底面圆半径，BC为高的圆锥AC为高的圆锥的侧面积为 S2,则（）A. S1= S2 B. S1 S2 C. Si S2 D. Si、S2 的大小关系不确定二、填空题cm，扇形的面积1.

14、扇形的弧长是 12刃cm,其圆心角是 90 ,则扇形的半径是是cm2.2. 扇形的半径是一个圆的半径的3倍，且扇形面积等于圆面积，则扇形的圆心角是.3. 已知扇形面积是12cm2,半径为8cm,则扇形周长为 .4在 ABC中，AB = 3, AC = 4,/ A = 90，把 Rt ABC绕直线 AC旋转一周得到一 个圆锥，其全面积为 S1 ；把Rt ABC绕AB旋转一周得到另一个圆锥，其全面积为 S2,则 S1 : S2= 。5. 一个圆柱形容器的底面直径为2cm，要用一块圆心角为 240的扇形铁板做一个圆锥形的盖子，做成的盖子要能盖住圆柱形容器，这个扇形的半径至少要有cm。6. 如图，扇形AOB的圆心角为60,半径为6cm, C, D分别是AB的三等分点，则阴 影部分的面积是。ft7.如图正方形的边长为 2,分别以正方形的两个对角顶点为圆心，以2为半径画弧，则阴影部分面积为 。三、计算题1.如图，在 Rt ABC中，AC = BC，以A为圆心画弧 线于点F,交BC于点E,若图中两个阴影部分的面积相等， 取3）。DF ,交AB于点D，交AC延长 求 AC与AF的长度之比（貝FSi,另一个圆锥的侧面积是S2,2. 一个等边圆柱（轴截面是正方形的圆柱）的侧面积是如果圆锥和圆柱等底等高，求.3. 圆锥的底面半径是 R，母线长是3R,