《三角函数的诱导公式》ppt课件

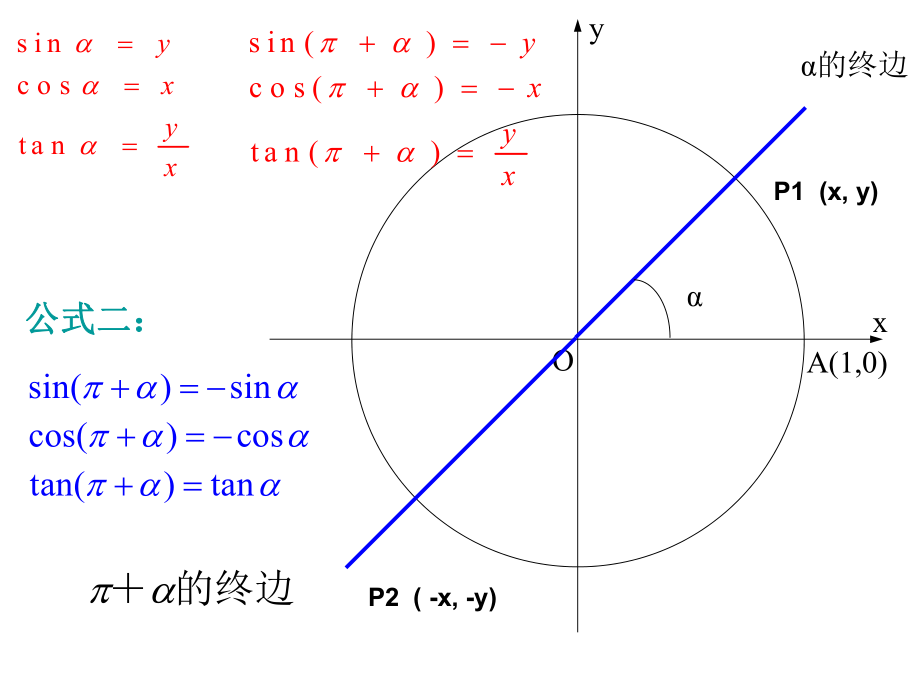
1、三角函数的诱导公式三角函数的诱导公式xyoP(x,y)(1,0)的终边 由定义有：由定义有：2.诱导诱导公式一公式一sincostanyxyx公式一公式一的用途的用途本节的内容本节的内容设设 0，那么，对于，那么，对于 90间的角，间的角， 180间的角，间的角， 270间的角，间的角，可表示成：可表示成：-可表示成：可表示成：可表示成：可表示成：-【探究探究】任意给定一个角 。（）角 的终边与角的终边有什么关系？（）它们的三角函数之间有什么关系？问题一： xOA(1,0)的终边P1 (x, y)P2 ( -x, -y)的终边s inc o sta nyxyxs in ()c o s ()ta

2、 n ()yxyx sin()sincos()costan()tan 公式二：公式二：y【探究探究】问题二：任意给定一个角。（）角 和 与角的终边有什么关系？（）它们的三角函数之间有什么关系？ yxOA(1,0)的终边P1 (x, y)P3 (x,-y)的终边s inc o sta nyxyxs in ()c o s ()ta n ()yxyx 公式三：公式三：tan)tan(cos)cos(sin)sin(yxOA(1,0)的终边P1 (x, y)P4 (-x, y)的终边s inc o sta nyxyxs in ()c o s ()ta n ()yxyx 公式四：公式四：tan)tan(

3、cos)cos(sin)sin(sinsin tantancoscos公式二：公式二：sin(2 ) sincos(2 ) costan(2 ) tankkk 公式一：公式一：公式三：公式三：tan)tan(cos)cos(sin)sin(公式四：公式四：tan)tan(cos)cos(sin)sin(诱导公式小结诱导公式小结公式一、二、三、四都叫做公式一、二、三、四都叫做诱导公式诱导公式概括如下：概括如下： 前面加上一个把看成锐角时原函数值的符号前面加上一个把看成锐角时原函数值的符号，的三角函数值，等于的同名函数值，的三角函数值，等于的同名函数值，2 (),kkz 简化成简化成“函数名不变，

4、符号看象限函数名不变，符号看象限”的口诀的口诀例利用公式求下列三角函数值：11(2)sin316(3)sin()30(4)cos( 2040 )0(1)cos225解:000021 cos225cos(18045 )cos452 （）113(2)sinsin(4)sin3332 1616(3) sin()sinsin(5)3333(sin)sin332 00000000(4)cos( 2040 )cos2040cos(6 360120 )1cos120cos(18060 )cos602 通过例题，你能说说诱导公式的作用以及化任意角通过例题，你能说说诱导公式的作用以及化任意角的三角函数为锐角三角

5、函数的一般思路吗？的三角函数为锐角三角函数的一般思路吗？ 小结小结任意负角的任意负角的 三角函数三角函数 任意正角的任意正角的 三角函数三角函数 20三角函数三角函数 的的锐角的三锐角的三角函数角函数用用公式公式三或一三或一用公式一用公式一用用公式公式二或四二或四上述过程体现了由未知到已知的上述过程体现了由未知到已知的化归化归思想。思想。练习1.cossin()sin(-)=cos5将下列三角函数转化为锐角三角函数，并填在题中横线上：13（1）（2）1+9（3）（4） (-70 6 )=4cos;9sin1;sin;5cos70 6;2.(1)cossinsincos利用公式求下列三角函数值：

6、（-420）7(2)（-）6(3)（330）79(4)（-）61cos420cos60cos602（360 +）=1sinsinsinsin2 77（-）=-（ +）=66661sin600sin(-30 )=-sin302 （3-3 ）=793coscos12()cos()cos66662 小结小结: (1) 探究三角函数诱导公式的推导过程,理解 “函数名不变，符号看象限函数名不变，符号看象限” (2)(2)熟悉将任意角的三角函数转化到锐角三角函 数的过程. (3) (3)熟练掌握三角函数的诱导公式. 作业：作业：1 cos(2)cos2 tan()tan(3)ABCABCABCAABC 思考：已知 、 、 是的三个内角，求证（：）（ ）P29 习题1.3 A组 2、3、4例2 化简：.)180cos()180sin()360sin()180cos(0000化简，解：先对各个因式进行,sin)360sin( ,cos)180cos(00)180(sin)180sin(00)180sin(0-sin)sin()180(cos)180cos(00)180cos(0cos. 1)cos(sinsincos原式提高题（2）已知，求的值336cos65cos（1）已知 ，且 是第一象限角， 求 的值 21c