第四章受弯构件正截面受力能

1、河南理工大学土木工程学院河南理工大学土木工程学院1 1、概述、概述overviewhfxbhfbfbfh0h承载力的观点：承载力的观点：挖去受拉区混凝土，形成挖去受拉区混凝土，形成T形截面，对受弯承载形截面，对受弯承载力没有影响。力没有影响。目的和好处：目的和好处：节省混凝土，减轻自重。节省混凝土，减轻自重。七、七、T形截面受弯构件形截面受弯构件河南理工大学土木工程学院河南理工大学土木工程学院七、七、T形截面受弯构件形截面受弯构件T形形截截面面梁梁的的应应用用河南理工大学土木工程学院河南理工大学土木工程学院T形截面梁翼缘内的压应力分布不均匀，且分布宽度与多种因素有关。形截面梁翼缘内的压应力分布

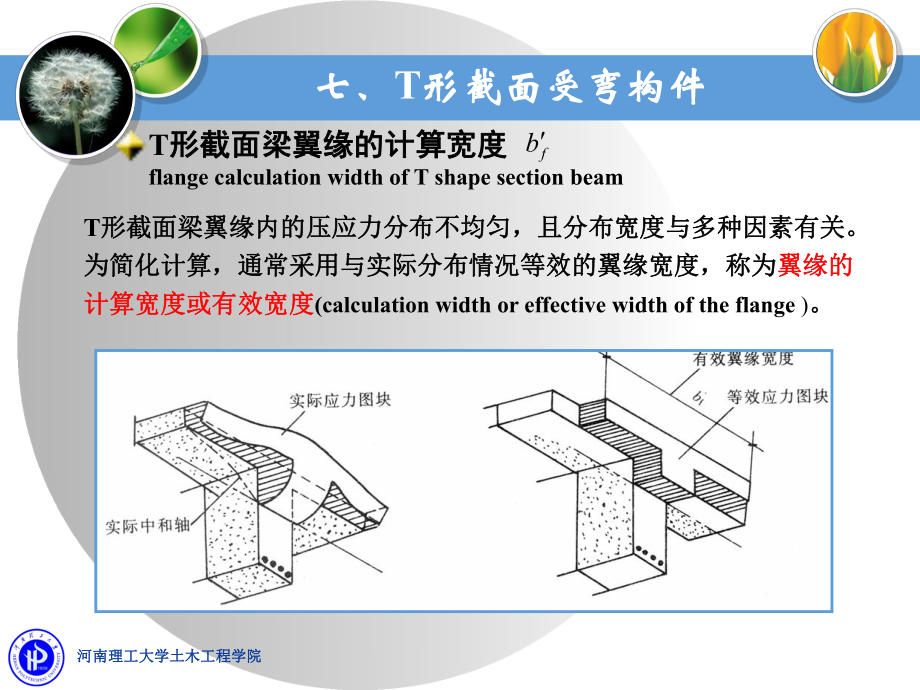
2、不均匀，且分布宽度与多种因素有关。为简化计算，通常采用与实际分布情况等效的翼缘宽度，称为为简化计算，通常采用与实际分布情况等效的翼缘宽度，称为翼缘的翼缘的计算宽度或有效宽度计算宽度或有效宽度(calculation width or effective width of the flange )。T形截面梁翼缘的计算宽度形截面梁翼缘的计算宽度flange calculation width of T shape section beamfb七、七、T形截面受弯构件形截面受弯构件河南理工大学土木工程学院河南理工大学土木工程学院T形截面梁翼缘的计算宽度形截面梁翼缘的计算宽度flange calcu

3、lation width of T shape section beamfb七、七、T形截面受弯构件形截面受弯构件l1l2河南理工大学土木工程学院河南理工大学土木工程学院T T形、工形、倒L形截面受弯构件翼缘计算宽度 fbT形截面倒L形截面考 虑 情 况肋形梁（板）独立梁肋形梁（板）按计算跨度l0考虑031l031l061l按梁（肋）净距Sn考虑nSb+nSb21+当1 . 00hhffhb+12当05. 01 . 00hhffhb+12fhb+6fhb+5按翼缘高度fh考虑当05. 00second type T-shaped section中和轴在梁肋内中和轴在梁肋内the neutral

4、 axis is in the beam rib七七、T形截面受弯构件形截面受弯构件2.2.计算简图和基本公式计算简图和基本公式calculation diagram and fundamental formula河南理工大学土木工程学院河南理工大学土木工程学院fhx第二类 T 形截面fhx界限情况截面设计截面设计截面校核截面校核第一类第一类T形截面形截面1yscfff Af b h 第二类第二类T形截面形截面1yscfff Af b h 10()2fcffhMf b hh 第二类第二类T形截面形截面10()2fcffhMf b hh 第一类第一类T形截面形截面七七、T形截面受弯构件形截面受弯

5、构件)5 . 0(011fffcusyffchhhbfMAfhbf两类两类T形截面判别形截面判别discrimination of two-type T section河南理工大学土木工程学院河南理工大学土木工程学院七七、T形截面受弯构件形截面受弯构件I类T形截面first type T-shaped sectionT形截面开裂弯矩与截面为腹板的矩形截面的开裂弯矩几乎相同xfyAsMu1fch0Asbfbhfh0as)2()2(0011xhAfxhxbfMAfxbfsyfcusyfc按bfh的矩形截面(rectangular section)计算bminbhAs对第一类对第一类T T 形截面，

6、该适用形截面，该适用条件一般能满足可不验算条件一般能满足可不验算河南理工大学土木工程学院河南理工大学土木工程学院七七、T形截面受弯构件形截面受弯构件 II类T形截面-和双筋矩形截面类似second type T-shaped section-similar to doubly reinforcement rectangular sectionxfyAsMuh01fcAsh0bfbhfasfyAs1Mu1xh01fcAs1h0basx21sssAAA+fyAs2h0As2(bf-b)/2bhfas(bf-b)/2hfMu2h01fc河南理工大学土木工程学院河南理工大学土木工程学院七七、T形截面受

7、弯构件形截面受弯构件II类T形截面-和双筋矩形截面类似second type T-shaped section-similar to doubly reinforcement rectangular sectionfyAs1Mu1xh01fcAs1h0basxfyAs2h0As2(bf-b)/2bhfas(bf-b)/2hfMu2h01fc+)2()()2()(01012111fffccuuusyffcchhhbbfxhbxfMMMAfhbbfbxf河南理工大学土木工程学院河南理工大学土木工程学院七七、T形截面受弯构件形截面受弯构件II类T形截面-和双筋矩形截面类似second type T-

8、shaped section-similar to doubly reinforcement rectangular sectionfyAs1Mu1xh01fcAs1h0basxfyAs2h0As2(bf-b)/2bhfas(bf-b)/2hfMfh01fc一般可自动满足,minbhx0河南理工大学土木工程学院河南理工大学土木工程学院七七、T形截面受弯构件形截面受弯构件minbhAsxfyAsM1fch0Asbfbhfh0as)2(01fffchhhbfM按按bfh单筋矩形截面进行设计单筋矩形截面进行设计design as the bfh singly reinforcement rectan

9、gular sectionfirst type T-shaped section3. 3. 公式的应用公式的应用-截面设计截面设计application of formula-section design121010()2cfysucfcfsf b xf AxMMf b x hf b h河南理工大学土木工程学院河南理工大学土木工程学院10121010()()()2ccffysucscfff bhf bb hf AhMMf bhf bb hh+10()2fcffhMf b hh second type T-shaped section同双筋矩形截面同双筋矩形截面2uM1uM2012bhfMMcu

10、ss211byffccsfhbbfbhfA101)(+b七七、T形截面受弯构件形截面受弯构件3. 3. 公式的应用公式的应用-截面设计截面设计application of formula-section design加大翼缘或梁高，重新计算加大翼缘或梁高，重新计算河南理工大学土木工程学院河南理工大学土木工程学院已知：已知： 、 、 、 、 、 、 、 求：求： bhfhfbsAyfMcfuM1yscfff Af b h 1100()()22cfysucfysf b xf AxxMMf b x hf A hfirst type T-shaped sectionbhAsmin10()2ucfxMf

11、 b x hminsAbh second type T-shaped section111010()()()()22ccffysfuccfff bxf bb hf AhxMMf bx hf bb hh+uM11()yscffcf Afbb hxf b0 bxh若：0 bxh若：0bxh取河南理工大学土木工程学院河南理工大学土木工程学院25208012585089029012530.425.4河南理工大学土木工程学院河南理工大学土木工程学院试验部分（理解）试验部分（理解） 适筋梁正截面受力三个阶段；适筋梁正截面受力三个阶段； 三种破坏形式的破坏特征和区分界限三种破坏形式的破坏特征和区分界限正截面承载力计算原则（理解）正截面承载力计算原则（理解） 基本假定；基本假定； 等效矩形应力图形；等效矩形应力图形； b意义及其用途意义及其用途summary河南理工大学土木工程学院河南理工大学土木工程学院单筋矩形截面正截面承载力计算（掌握）单筋矩形截面正截面承载