C语言迪杰斯特拉实现最短路径算法

1、数据结构课程设计报告-旅游咨询系统设计目录一、需求分析 - 2 -二、系统分析 - 2 -三、概要设计 - 3 -一、 系统划分 - 3 -二、 邻接矩阵建立流程图： - 3 -三、 迪杰斯特拉算法流图 - 5 -四、详细设计 - 6 -五、调试分析 - 9 -一、运行结果 - 9 -二、改进设想 - 13 -六、课设总结 - 13 -旅游咨询系统设计一、需求分析 在交通网络日益发达的今天，人们出行有很多种方式、路线，而如何选择符合需要的方式路线成为大家的一大难题。所以，在此我利用计算机建立一个旅游咨询系统。在系统中采用图来构造各个城市之间的联系，图中顶点表示城市，边表示各个城市之间的路线，所

2、带权值为两个城市间的路程、时间或车费等。这个交通咨询系统可以回答旅客提出的各种问题，例如：如何选择一条路径使得从A城到B城里程最短；如何选择一条路径使得从A城到B城花费最低；如何选择一条路径使得从A城到B城所用的时间最少等等的一系列问题。二、系统分析设计一个旅游咨询系统，能咨询从任何一个城市顶点到其他城市顶点之间的最短路径(里程、最低花费或是最少时间等问题。对于不同的咨询要求，可输入城市间的路程、所需时间或是所需费用等信息。旅客可以在同一个系统中综合考虑自己的各目标城市，选择一个最佳的旅游路线和出行方式。针对最短路径问题，在本系统中采用图的相关知识，采用了迪杰斯特拉算法，解决在实际情况中的最短

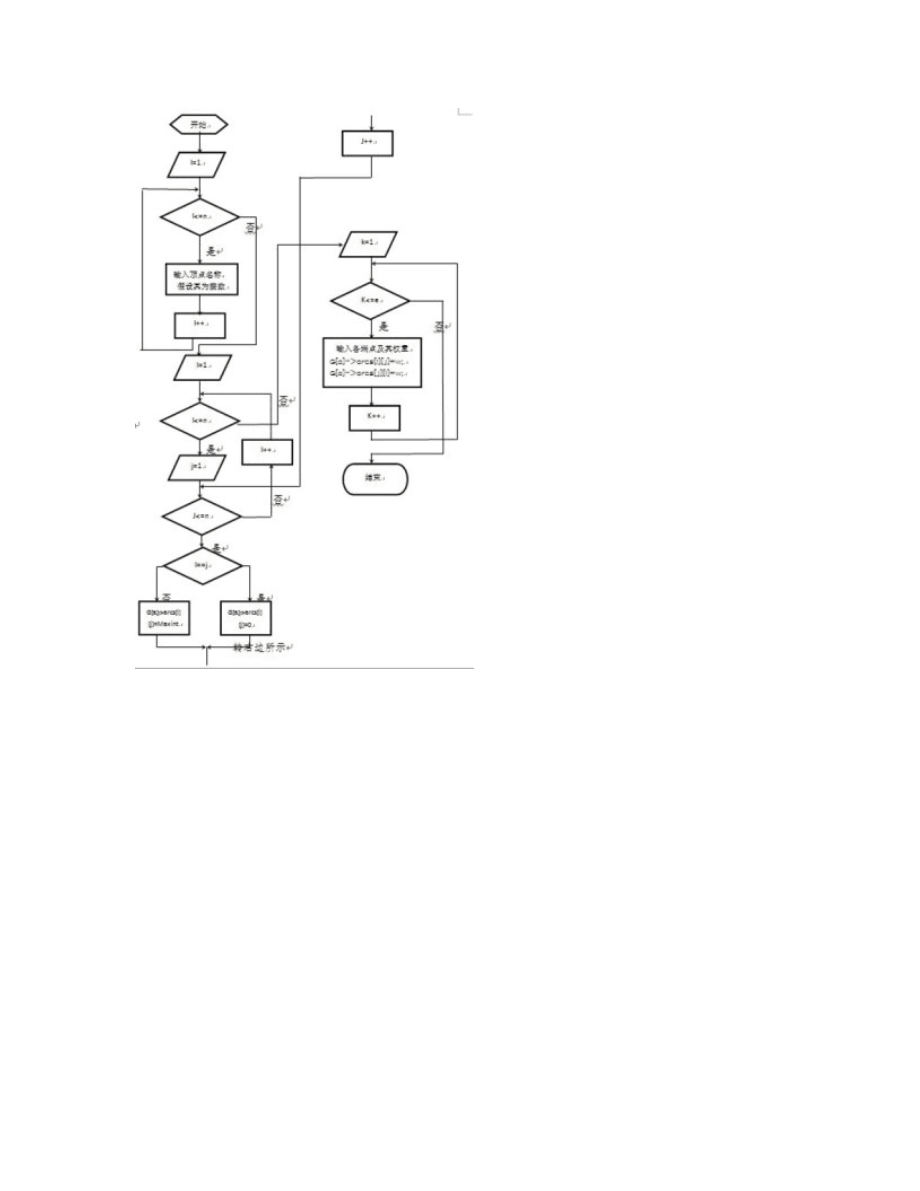
3、路径问题，而迪杰斯特拉算法的时间复杂度为O(n2,空间复杂度为O(n。本系统使用邻接矩阵存储无向图。其中，建立矩阵的时间复杂度为O(n2,但是利用其查找一条边的时间复杂度为O(1。本系统中包括了利用邻接矩阵建立图的存储结构和单源最短问题两大部分，使用指针数组实现利用一个程序实现最短路径和最短时间的运算。并且本系统设置了人性化的系统提示菜单，方便使用者的使用。三、概要设计一、 系统划分该系统可以划分为三个部分：1、 利用邻接矩阵建立图的存储结构；2、 利用迪杰斯特拉算法解决单源最短路径问题；3、 实现城市之间的最短路径问题和最短时间问题。二、 邻接矩阵建立流程图：四、详细设计本课程设计的源程序如

4、下所示：#include #include #define MVNum 100#define Maxint 9999 /*将无穷大的数值设为9999*/typedef char vertextype;/*建立无向图*/typedef int adjmatrix;typedef structvertextype vexsMVNum;adjmatrix arcsMVNumMVNum;mgraph;mgraph *G2; /*设置指针数组用以实现距离和时间最小值求取*/void city_number( /*输出城市代表序号*/ printf("*n"printf("

5、1、北京 2、上海 3、香港 4、天津 5、重庆 6、澳门 7、哈尔滨 8、石家庄"printf(" n 9、兰州 10、昆明 11、成都 12、长春 13、沈阳 14、长沙 15、海口 16、西安"printf("n*n"void Createmgraph(int a,int n,int e /*建立无向邻接矩阵*/int i,j,k;int w;for(i=1;i<=n;i+for(j=1;j<=n;j+if(i=j Ga->arcsij=0; /*邻接矩阵对角线初始值设为0*/else Ga->arcsij=Max

6、int; /*其他元素设为无穷大*/for(k=1;k<=e;k+ /*读入e条边数的信息*/printf("n输入图中各起点终点及其权值i,j,w:" /*读入无向边及其权值*/scanf("%d,%d,%d",&i,&j,&w;Ga->arcsij=w; Ga->arcsji=w;void Dijkstra(int a,int v0,int N/*Dijkstra算法的实现和打印*/enum boolean SMVNum; /*终点集合*/int distMVNum,pathMVNum; /*dist表示源点

7、v0到图中其余顶点的最短长度，path表示其对应的路径*/int i,wmin,u,num=1,k;for(i=1;i<=N;i+ /*数组dist和集合S付初值*/disti=Ga->arcsv0i; /*数组dist初值为邻接矩阵*/Si=0; /*集合S初值设为空集*/if(disti else pathi=0;Sv0=1; /*源点v0放入集合S中*/pathv0=0;dowmin=Maxint; /*wmin最小值设为无穷大*/u=v0;for(i=1;i<=N;i+if(Si=0 /*选择不在S中且距离最小的顶点u*/if(disti u=i;wmin=disti

8、;Su=1; /*把距离最小的顶点u放入集合S中*/for(i=1;i<=N;i+ /*修改不在S中的顶点距离*/if(Si=0if(distu+Ga->arcsui disti=distu+Ga->arcsui;pathi=u;num+;while(num<=N;printf("nt输出带权无向图的单元最短路径为:nt"/*打印v0到其他顶点的最短路径*/for(i=1;i<=N;i+if(Si=1k=i;printf("nt顶点%d到%d之间的路径为:",v0,i;while(k!=v0printf("%d&l

9、t;-",k; /*输出后继顶点*/k=pathk; /*继续寻找下一个后继顶点*/printf("%d",k; /*输出终点*/printf(",最短路径长度为%dn",disti; /*输出最短路径*/else printf("nt顶点%d到%d之间没有路径！",v0,i;printf("nt求一个城市到所有城市的最短路径结束，谢谢！nntt"void main( /*旅游咨询系统*/int n,e,v,u,i,x;int z=0;G1=(mgraph *malloc(sizeof(mgraph; /

10、*建立类型为mgraph的十字链表结构*/G2=(mgraph *malloc(sizeof(mgraph;printf("*欢迎使用旅游咨询系统*n"printf("输入图中顶点个数和边数n,e:"scanf("%d,%d",&n,&e;city_number(;for(i=1;i<=n;i+ /*输入顶点信息*/printf("n请输入图的所有顶点i="scanf("%d",&x;G1->vexsi=x; /*将顶点信息输入一维数组中*/G2->ve

11、xsi=x;printf("n请输入距离矩阵的数值n"Createmgraph(1,n,e; /*建立距离矩阵*/ printf("n距离矩阵建立完毕n请输入时间矩阵的数值"Createmgraph(2,n,e; /*建立时间矩阵*/printf("n无向图的存储结构建立完毕！n"do printf("nnn*进行最短查询*n"printf("=n"printf("1.求一个城市到所有城市的最短路径n"printf("2.求一个城市到所有城市的最短时间n"

12、printf("3.退出n"printf("=n"printf("请输入选择:"scanf("%d",&z; /*输入选择选择矩阵*/city_number(;if(z=1 printf("n选择1 求一个城市到所有城市的最短路径n"printf("求单源路径,输入源点v :" /*输入源点v0*/scanf("%d",&v;Dijkstra(1,v,n; /*计算最短距离*/else if(z=2 printf("n选择2 求一

13、个城市到所有城市的最短时间n"printf("求单源路径,输入源点,u :"scanf("%d",&u;Dijkstra(2,u,n; /*计算最短时间*/ else if(z=3printf("n结束查询!谢谢使用!n"else printf("输入错误!n" /*输入不为1-3则重新选择*/ while(z!=3; /*输入3则退出*/printf("谢谢您的使用,再见!n"五、调试分析一、运行结果1、 输入顶点总数为6，边的总数为10，并输入顶点信息。2、 输入距离矩阵的

14、端点 以及其权值w。3、 输入时间矩阵的端点 以及其权值w。4、 邻接矩阵建立完毕。输入选择1求城市3即香港到其他城市的最短路径。5、 求解城市3即香港到其他城市的最短路径结果如图所示。6、 输入选择2求城市3即香港到其他城市的最短时间。7、 求解城市3即香港到其他城市的最短时间结果如图所示。8、 输入选择3退出旅游咨询系统。二、改进设想由于本系统为旅游咨询系统，所以可以添加一个排序算法将所有输入的方案储存起来并且综合进行排序，选出最符合要求的目标城市。此外，以数字代替城市名在查询的时候仍然不是很方便，如果能用数组储存好城市名，然后调用数组显示城市名将更方便查询。最后，还可以考虑加一个算法得出

15、中转站最多和最少的路线。六、课设总结本次课程设计已经进入尾声，通过这次课程设计，我对图的概念有了新的认识，对于数据结构这门课程也有了进一步的了解。这次课程设计从选材到实施我都遇到了一些小问题。首先是选材问题，数据结构这门课程涉及很广，运用的方面也很多。刚开始我准备利用双向链表建立一个学生宿舍管理系统，但是很快我就觉得这个方案没有亮点和新意，而当时我们正在学习图，我也对它的应用感到有兴趣，于是，我决定利用图求最短路径。在我和其他同学进行交流后发现大家做图的人也不少，但是大家大都偏向于Floyd算法。所以我决定使用Dijkstra算法来完成。很快我就发现这个算法的资料很少，即使有，也是C+程序的。

16、但是我没有退却，我从书本中找到Dijkstra算法的实现程序，细细研究，将它每句程序都研究透彻，再联合邻接矩阵将算法实现。我首先将Dijkstra算法和邻接矩阵写成子程序形式，利用主程序将他们联系在一起，用以实现最短距离的求取，但是，我发现地点没办法表示在屏幕上。在我和老师进行交流时，老师建议我利用数字代替城市进行输出，并且尝试一下完成时间最短的求取。我采取老师的建议利用数字代替城市进行输出，并且思考如何利用同一个程序完成距离最短和时间最短的求取，然后我想到了C语言中学习到的指针数组，于是我利用G1指向距离矩阵，G2指向时间矩阵来完成要求。最后，我在进行调试的时候发现当我再输入I,j,w值时如

17、果输入的数值为1,2,2（即1城市到2城市的距离为2）和2,3,3（即2城市到3城市的距离为3）时，系统输出显示从1->3没有路径，而3->1有路径，而如果我输入1,2,3,和2,3,2时，系统输出显示从1->3有路径，而3->1没有路径。在进行多次试验并确认矩阵算法没有错误后，我锁定错误出现在Dijkstra算法中的将最短距离顶点放入集合S中的那段程序中。在我仔细检查程序后发现书上我所参考的程序语句if（(distu+Ga->arcsui Ga->arcsui 出现错误，因为，此时 wmin 为 distu 的值。以我所列举的第一种情况为例，在讨论源点为 1 终点为 3 时，即要求为 2+3 小于无穷大，并且 3<2, 显然不成立，所以输出 1->3 没有路径。 完成了课程设计后。我觉得我收获不少，首先是不能人云亦云，看见别人做什么于是也跟着干什么，得有自己的新意，做出自己的风格；其次，遇到问题不要马上想到求助，应该自己冷静下来想想应该如何靠自己的力量解决；再者，在调试程序甚至干其他