二重积分的计算法

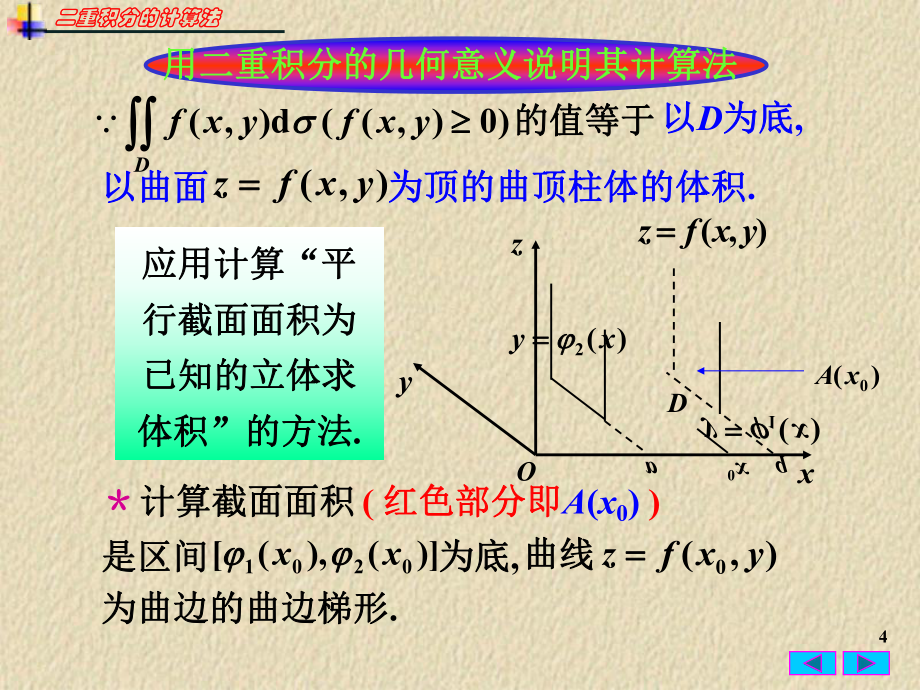
1、1利用直角坐标系计算二重积分利用直角坐标系计算二重积分小结思考题小结思考题 作业作业利用极坐标系计算二重积分利用极坐标系计算二重积分double integral二重积分的换元法二重积分的换元法第二节第二节 二重积分二重积分的计算法的计算法第八章第八章 重积分重积分2本节介绍计算二重积分的方法本节介绍计算二重积分的方法:二重积分化为二重积分化为累次积分累次积分( (即两次定积分即两次定积分).).二重积分的计算法二重积分的计算法3(1) 积分区域积分区域为：为：, bxa ).()(21xyx 其中函数其中函数 、)(1x )(2x b)(2xy )(1xy aDX型型,ba在区间在区间 上连

2、续上连续.二重积分的计算法二重积分的计算法一、利用直角坐标系计算二重积分一、利用直角坐标系计算二重积分xOyxOy)(1xy )(2xy Dba4的的值值等等于于)0),(d),( yxfyxfD 计算截面面积计算截面面积),(yxfz ( 红色部分即红色部分即A(x0) )二重积分的计算法二重积分的计算法以以D为底为底,以曲面以曲面为顶的曲顶柱体的体积为顶的曲顶柱体的体积.应用计算应用计算“平平行截面面积为行截面面积为已知的立体求已知的立体求体积体积”的方法的方法.用二重积分的几何意义说明其计算法用二重积分的几何意义说明其计算法是区间是区间)(),(0201xx 为曲边的曲边梯形为曲边的曲边

3、梯形.),(0yxfz 为底为底,曲线曲线 xyzO),(yxfz D)(1xy )(2xy ab0 x)(0 xA5是区间是区间 为底为底,)(),(0201xx 曲线曲线 为曲边为曲边 的曲边梯形的曲边梯形.),(0yxfz )(01x ,bax yyxfxAxxd),()()()(21 有有: DyxfV d),( baxxAd)(xbad 二重积分的计算法二重积分的计算法)d),()()(21 xxyyxf )(02x yyxfxAd),()(00 先对先对y后对后对x的二次积分的二次积分称为称为累次积分累次积分. . Dyxf d),( baxxyyxfx)()(21d),(d xy

4、zO),(yxfz D)(1xy )(2xy ab0 x)(0 xA6(2) 积分区域积分区域为：为：,dyc )()(21yxy D)(2yx cd)(1yx Y型型 Dyxf d),(先对先对x后对后对y的二次积分的二次积分也即也即 dcyyxyxfy)()(21d),(d Dyxf d),(二重积分的计算法二重积分的计算法其中函数其中函数 、)(1y )(2y ,dc在区间在区间 上连续上连续.xOyxOyD)(2yx cd)(1yx dcyd)d),( xyxf)(1y )(2y 7特殊地特殊地 Dbadcyyxfxyxfd),(dd),( 如如D是上述矩形域是上述矩形域, )()()

5、,(21yfxfyxf 且且得得 yxyfxfDdd)()(21即等于两个定积分的乘积即等于两个定积分的乘积.注注D为矩形域为矩形域:则则则则axb,cyd baxxfd)(1yyfdcd)(2 二重积分的计算法二重积分的计算法 yyfxfdcd)()(21 ba(xd) ba(xd)d( , )ddbcayf x yx12( )( )ddcf xfyy8穿过区域且平行于穿过区域且平行于y轴的直线轴的直线穿过区域且平行于穿过区域且平行于x轴的直线轴的直线abdc 计算结果一样计算结果一样.又是又是Y型型:(3)积分区域积分区域D既是既是X型型:, bxa )()(21xyx , dyc )()

6、(21yxy X型区域的特点型区域的特点:Y型区域的特点型区域的特点:与区域边界相交不多于两个交点与区域边界相交不多于两个交点.与区域边界相交不多于两个交点与区域边界相交不多于两个交点.但可作出但可作出适当选择适当选择.二重积分的计算法二重积分的计算法xyO9(4) 若区域如图若区域如图,在分割后的三个区域上分别在分割后的三个区域上分别使用积分公式使用积分公式. D(用积分区域的可加性质用积分区域的可加性质)D1、D2、D3都是都是X型区域型区域则则必须分割必须分割. 321DDD二重积分的计算法二重积分的计算法xyO3D2D1D10 xyO例例解解 Dyxyxdd)(2xxxxxxd)(21

7、)(42102 .14033 积分域既是积分域既是X型又是型又是Y型型 22xyyx yyxd)(2 10dx法一法一)0 , 0(),1 , 1(所围平面闭区域所围平面闭区域.和和是是抛抛物物线线其其中中求求22,dd)(xyDyxyxD 2yx 两曲线的交点两曲线的交点2xx二重积分的计算法二重积分的计算法2xy 2yx )1 , 1( 11先对先对x后对后对y的积分的积分 Dyxyxdd)(214033 10dy法二法二 xyxd)(22yy二重积分的计算法二重积分的计算法 Dyxyxdd)(2xyO2xy 2yx )1 , 1( 12例例yyxxdsind1012 siny2 对对y的

8、积分的积分而它对而它对x的积分的积分交换积分次序交换积分次序的方法是的方法是:改写改写D为为:oxy 分析分析所以将所以将二次积分二次积分先先将所给的积分域将所给的积分域(1)(2) 画出积分域的草图画出积分域的草图(3)计算二次积分计算二次积分不能用基本积分法算出不能用基本积分法算出,xy )1 , 1(可用基本积分法算出可用基本积分法算出.交换积分次序交换积分次序. .用联立不等式表示用联立不等式表示 D:, 10 x1 yx, 10 yyx 0二重积分的计算法二重积分的计算法13yyxxdsind1012 yxyyd)(sin0102 yyydsin102 2102dsin21yy )1

9、cos1(21 xyydsin02 10dyoxyxy )1 , 1(, 10: yDyx 0二重积分的计算法二重积分的计算法14例例 交换积分次序：交换积分次序：解解 积分区域积分区域: xxxyyxfxyyxfx20212010d),(dd),(d2原式原式= 10dyy 2 xyxfd),(211y 二重积分的计算法二重积分的计算法22xxy xy 2xyO1215例例axy2 22xaxy 22yaax 解解原式原式= xyxfd),(交换积分次序：交换积分次序： axxaxayyxfx22202d),(d)0( a yday22xyxfd),( 22yaa 0aa222yaa yd0

10、a xyxfd),( yda2ay22a2a二重积分的计算法二重积分的计算法xyOaa2aa2ayx22 16交换积分次序的步骤交换积分次序的步骤 (1) 将已给的二次积分的积分限得出相将已给的二次积分的积分限得出相应的二重积分的积分区域应的二重积分的积分区域,(2) 按相反顺序写出相应的二次积分按相反顺序写出相应的二次积分.并画出草图并画出草图;二重积分的计算法二重积分的计算法17二重积分的计算法二重积分的计算法二次积分一定能交换次序二次积分一定能交换次序答答 不一定不一定!例如例如: .0, 0,0,)(),(222222222时时当当时时当当设设yxyxyxyxyxf,d ),(d101

11、01yyxfxI 由于由于 22yxyy故故 yyxfd),(10 102d11xx yyxfxId ),(d10101所以所以,4 ),(yxf10arctan x yyxyyd1022 1022yxy;112 x18二重积分的计算法二重积分的计算法例如例如: .0, 0,0,)(),(222222222时时当当时时当当设设yxyxyxyxyxf yyxfxId ),(d10101,4 ,d ),(d10102xyxfyI 由于由于 22yxxx故故 xyxfd),(10 yy102d11所以所以.4 xyxfyId ),(d10102 yyxfxd ),(d1010.d ),(d1010

12、xyxfy ),(yxf xyxxxd1022 1022yxx;112y 10arctan y 说明说明: :当当f (x, y)在所考虑的区域上连续时在所考虑的区域上连续时,二次积分可以交换积分次序二次积分可以交换积分次序.191990 年研究生考题年研究生考题, 填空填空, 3分分)(dd2202 yexxy)1(214 exy xoy22解解yexxydd2202 xeyyydd0202 yyeyd202 )(d212202yey )1(214 e二重积分的计算法二重积分的计算法交换积分次序交换积分次序2200dyyexy20又是能否进行计算的问题又是能否进行计算的问题. .计算二重积分

13、时计算二重积分时, , 恰当的选取积分次序恰当的选取积分次序十分重要十分重要, , 它不仅涉及到计算繁简问题它不仅涉及到计算繁简问题, , 而且而且凡遇如下形式积分凡遇如下形式积分: :,dsinxxx ,d2xex ,lnd xx等等等等, ,一定要放在一定要放在后面积分后面积分. .,dsin2xx ,dcos2xx ,d2xex ,dxexy 二重积分的计算法二重积分的计算法21例例 求证求证 axaxxfxayyfx000d)()(d)(d 左边的累次积分中左边的累次积分中,积分域积分域可表为可表为提示提示 xayyfx00d)(d ayaxyfyd)(d0 ayyfya0d)()(

14、axxfxa0d)()(定积分与积分变量的记法无关定积分与积分变量的记法无关不能具体计算不能具体计算.所以所以,)(yf是是y的抽象函数的抽象函数,)0( a,0ax xy 0,0ay axy aayyxyf0d)(证毕证毕.先交换积分次序先交换积分次序. .二重积分的计算法二重积分的计算法axyOa),(aa 22例例 求两个底圆半径为求两个底圆半径为R,且这两个圆柱面的方程且这两个圆柱面的方程分别为分别为 及及222Ryx .222Rzx 解解 d DyxRd22 332R 313168RVV d),(1 DyxfV22xRy 222Rzx 立立体体顶顶部部222Ryx 立立体体底底部部求

15、所围成的求所围成的立体的体积立体的体积.xoyzoxyDR22xR 22xR 0 xd0R二重积分的计算法二重积分的计算法22xRz 曲曲顶顶还有别的做法吗还有别的做法吗23二重积分的计算法二重积分的计算法2002 年研究生考题年研究生考题, 7分分计算二重积分计算二重积分,dd,max22 Dyxyxe其中其中.10 , 10),( yxyxDxyO 解解 112D1D设设, 10),( 1 xyxDxy 0, 10),( 2 xyxD1 yx Dyxyxedd,max22 122dd,maxDyxyxe 222dd,maxDyxyxe 12ddDxyxe 22ddDyyxe xxyex01

16、0dd2 yyxey010dd2. 1 e xxyex010)dd2(2或或24解解 121d)(xeexxee2183 xeyxeyIyyxyyxydddd121212141 计算积分计算积分xexyd 不能用初等函数表示不能用初等函数表示,先交换积分次序先交换积分次序.yexyd x2x xd I211二重积分的计算法二重积分的计算法112141xy 2xy 21Oxyi25i ii i iiii )2(21iiiii 2)(iii 两相邻弧半径平均值两相邻弧半径平均值. i 内取圆周内取圆周上一点上一点其直角坐标其直角坐标, ii),(ii iii 2)(21ii 221则则设为设为二重

17、积分的计算法二重积分的计算法二、利用极坐标系计算二重积分二、利用极坐标系计算二重积分OADi ii i ),(ii iiii i26得得 iiinif ),(lim10即即 Dyxf d),( Dyxyxfdd),(也即也即 dd极坐标系中的面积元素极坐标系中的面积元素,cosiii iiii Df dd)sin,cos( Df dd)sin,cos( nif1(,cosii iii )sinii 0lim 二重积分的计算法二重积分的计算法siniii27 )(1 )(2 Df dd)sin,cos(1) 积分区域积分区域D:, )()(21 AO)(1 )(2 D d)(1 d)sin,co

18、s(f)(2 二重积分的计算法二重积分的计算法OAD28D )(0d)sin,cos(d f(2)积分区域积分区域D(曲边扇形曲边扇形):, )(0 Df dd)sin,cos(AOAO 二重积分的计算法二重积分的计算法D ( ) ( ) 29 Df dd)sin,cos( )(020d)sin,cos(d f极坐标系极坐标系下区域的下区域的面积面积 D dd(3) 积分区域积分区域D:,20 )(0 DoA)( 注注一般一般,在极坐标系下计算在极坐标系下计算:积积分分再再对对先先对对 二重积分的计算法二重积分的计算法30解解 sincosyx Dyxyxfdd),( d)sin,cos(df

19、例例 写出积分写出积分的的极坐标二次积分极坐标二次积分 Dyxyxfdd),(其中积分区域其中积分区域形式形式,10 ,11),(2 xxyxyxD在极坐标系下在极坐标系下圆方程为圆方程为1 直线方程为直线方程为 sincos1 1 cossin1 02 二重积分的计算法二重积分的计算法yxO11122 yx1 yxD31解解yxeDyxdd22 ae020dd2 )1(2ae a例例 计算计算,dd22yxeDyx 其中其中D是由中心在原点是由中心在原点,半径为半径为a的圆周所围成的闭区域的圆周所围成的闭区域.在极坐标系下在极坐标系下:D,20 a 0二重积分的计算法二重积分的计算法xOy3

20、2R2解解0, 0,| ),(2221 yxRyxyxD0, 0,2| ),(2222 yxRyxyxD0 ,0| ),(RyRxyxS 022 yxe Syxyxedd22 222ddDyxyxe求反常积分求反常积分.d02xex 例例显然有显然有21DSD 二重积分的计算法二重积分的计算法 122ddDyxyxeR1DS2DyxO33 Rxxe0d220)d(2 Rxxe)1(2Re yxeDyxdd22 )1(2ae 222:ayxD 又又yxeISyxdd22 yxeIDyxdd1221 yxeIDyxdd2222 )1(422Re 4 Ryye0d2 二重积分的计算法二重积分的计算法

21、0, 0,| ),(2221 yxRyxyxD0, 0,2| ),(2222 yxRyxyxD对称性对称性质质0 ,0| ),(RyRxyxS 34,41 I42 I,4 I21III )1(4)d()1(4222220RRxRexee 概率积分概率积分夹逼定理夹逼定理,时时当当 R,时时故故当当 R即即4)d(202 Rxxe所求反常积分所求反常积分2d02 xex),1(421ReI )1(4222ReI ,)d(202 RxxeI二重积分的计算法二重积分的计算法3503 yx解解32 61 sin4 sin2 yxyxDdd)(22 dd2)32(15 03 xy计算计算,dd)(22y

22、xyxD 为为由由圆圆其其中中D所围成的平面闭区域所围成的平面闭区域.例例yyxyyx4,22222 及直线及直线, 03 yx03 xy sin4 sin26 3 二重积分的计算法二重积分的计算法xOyyyx222 yyx422 36解解)(2)(222222yxayx 222ayx 双纽线双纽线求曲线求曲线)0()(2)(222222 ayxayx222ayx 和和所围成的图形的面积所围成的图形的面积.例例根据对称性有根据对称性有14DD 在极坐标系下在极坐标系下1Da 2cos2a 二重积分的计算法二重积分的计算法xyO由由 aa 2cos2得交点得交点)6,( aA yxdd)33(2

23、 a Dyxdd 2cos20dd46aa41D面积面积A37将将直角坐标系直角坐标系下累次积分下累次积分: 22240214110d),(dd),(dxxxyyxfxyyxfx化为化为极坐标系极坐标系下的下的累次积分累次积分.oxy解解 2120d)sin,cos(df原式原式=2 r21 r1二重积分的计算法二重积分的计算法381994年研究生考题年研究生考题, 填空填空, 3分分yxbyaxRyxDDdd,2222222 则则为为圆圆域域设设)( yxbyaxDdd2222 解解 dsincosd20222220 Rba 2241141baR 极坐标极坐标二重积分的计算法二重积分的计算法

24、39计算二重积分计算二重积分,dd)sin(22)(22 DyxyxyxeI 二重积分的计算法二重积分的计算法2003年研究生考题年研究生考题(数学三、四数学三、四)计算计算, 8分分其中积分区域其中积分区域.),( 22 yxyxD答案答案).1(2 eI 404 计算计算16:22 yxD因被积函数因被积函数422 yx4:221 yxD164:222 yxDD2 d)4(221yxID d)4(222 yxD极坐标极坐标 d|4|22 DyxI例例分析分析故故 80 422 yx的的在积分域内变号在积分域内变号.2xoyD1二重积分的计算法二重积分的计算法41 计算计算,dd|)|(|

25、Dyxyx0, 1|:| xyxD解解 积分区域积分区域D关于关于x轴对称轴对称,被积函数关于被积函数关于y为偶函数为偶函数.原式原式=记记D1为为D的的y0的部分的部分. yxyxdd|)|(| 1dd)(2Dyxxy xyxyx1001d)(d2则则21D32 xyoD111 1 yx1 1 yx二重积分的计算法二重积分的计算法42 二重积分的计算规律二重积分的计算规律再确定交换积分次再确定交换积分次1. 交换积分次序交换积分次序:先依给定的积分次序写出积分域先依给定的积分次序写出积分域D的的不等式不等式, 并画并画D的草图的草图;序后的积分限序后的积分限;2. 如被积函数为如被积函数为圆

26、环域时圆环域时,或积分域为或积分域为),(22yxf ),(22yxf ),(xyf)(arctanxyf圆域、扇形域、圆域、扇形域、则用极坐标计算则用极坐标计算;二重积分的计算法二重积分的计算法43 3. 注意利用对称性质注意利用对称性质,数中的绝对值符号数中的绝对值符号.以便简化计算以便简化计算;4. 被积函数中含有绝对值符号时被积函数中含有绝对值符号时, 应应将积分域分割成几个子域将积分域分割成几个子域, 使被积函数在使被积函数在每个子域中保持同一符号每个子域中保持同一符号, 以消除被积函以消除被积函二重积分的计算法二重积分的计算法44例例 计算计算,d)1(2322 DyxyI10 ,

27、 10: yxD 分析分析 从被积函数看从被积函数看,用极坐标系要简单些用极坐标系要简单些,但从积分域但从积分域D的形状看的形状看为宜为宜.用却又以直角坐标系用却又以直角坐标系在两者不可兼得的情况下在两者不可兼得的情况下,应以应以D的形状的形状来决定用什么坐标系来决定用什么坐标系,此题用直角坐标系此题用直角坐标系.xyo)1 , 0()0 , 1(D二重积分的计算法二重积分的计算法45 101021 d)1(2322 DyxyIxyxd11101022 xxxd)1121(2102 3122ln 二重积分的计算法二重积分的计算法xyo)1 , 0()0 , 1(xd232222)1()1(dy

28、xyx 46二重积分的计算法二重积分的计算法2003年研究生考题年研究生考题(数学三、四数学三、四)填空填空, 4分分 , 0, 10,)()(, 0其其它它若若设设xaxgxfa而而D表示全平面表示全平面,则则).(dd)()( DyxxygxfI2a47三、三、二重积分的换元法二重积分的换元法设被积函数设被积函数),(yxf在区域在区域D上连续上连续,若变换若变换),(),(vuyyvuxx 满足如下条件满足如下条件:(1)的的点点平平面面上上的的区区域域将将 DuOv一对一地变为一对一地变为D上的点上的点;(2),(),(vuyvux上上在在 D有连续的一阶偏导数有连续的一阶偏导数,且雅

29、可比行列式且雅可比行列式 ),(),(vuyxJvyuyvxux Dyxf d),(0 f D),(vux),(vuy| Jvudd二重积分的计算法二重积分的计算法48,1的的形形状状于于积积分分区区域域作作什什么么变变换换主主要要取取决决D基本要求基本要求. 2 注意注意变换后定限简便变换后定限简便,的形式的形式同时也兼顾被积函数同时也兼顾被积函数),(yxf的性质的性质J ),(),(vuyxJ),(),(1yxvu 求积容易求积容易二重积分的计算法二重积分的计算法49例例解解,dd12222yxbyaxD 计计算算 20, 0, 0, 0 ba其其中中 sincosbyax在这变换下在这

30、变换下所围成的闭区域所围成的闭区域.12222 byaxD20,10),( rD D二重积分的计算法二重积分的计算法xyO其中其中D为椭圆为椭圆作作广义极坐标广义极坐标变换变换50 ),(),( yxJ,0处处为为零零内内仅仅当当在在 rDJ yxbyaxDdd12222ab 32 ab sincosbyax yyxx故换元公式仍成立故换元公式仍成立, DDvuJvuyvuxfyxyxfdd),(),(dd),(21 ab dd D 10220d1d ab极坐标极坐标二重积分的计算法二重积分的计算法 DxyO51例例解解轴轴和和轴轴、由由其其中中计计算算yxDyxeDxyxy,dd ,2uvx

31、 Dxyo2 yx Duvo0 y2 yx.2所围成的闭区域所围成的闭区域直线直线 yx,xyu 令令xyv 则则2uvy 即即0 xvu vu vu 2 vvu 2 vDD二重积分的计算法二重积分的计算法52),(),(vuyxJ ,21 Dxyxyyxedd vvvuuevdd2120 201d)(21vvee1 ee2,2uvyuvx 21212121 vyuyvxux uvovu vu 2 v D Dvue故故vudd21 二重积分的计算法二重积分的计算法53,)( 为连续函数为连续函数设设tf证明证明 Daattatfyxyxfd|)|)(dd)().0(2| ,2| aayaxD常

32、常数数为为矩矩形形域域：其其中中xoy证证2ax 2a2a2a 法一法一 Dyxyxfdd)( 2222d)(daaaayyxfxtyx 22daaxtydd 2ax 2a ttfd)(交换积分次序交换积分次序xot2a 2a2a2a xttfdd)( xttfdd)(0a 2a 2at 2at 0a2a累次积分累次积分D二重积分的计算法二重积分的计算法54 xttfdd)( xttfdd)(0a 2a 2at 2at 0a2a 0d)(atattf atattf0d)( aattatfd|)|)( Daattatfyxyxfd|)|)(dd)(:证明证明 0d)|)(atattf atatt

33、f0d)|)(二重积分的计算法二重积分的计算法55aa a a,)( 为连续函数为连续函数设设tf证明证明 Daattatfyxyxfd|)|)(dd)().0(2| ,2| aayaxD常常数数为为矩矩形形域域：其其中中法二法二xoy2a2a2a 2a D令令, yxu yxv 则则 DD: D,avua auva ),(),(vuyxJ D21),(),(1 yxvuuov二重积分的计算法二重积分的计算法56故故 Dyxyxfdd)( Dvuufdd21)(21 J, yxu . yxv aa a auov对称性对称性 00dd)(21auavuuf Davu avu auavuuf00d

34、d)(21 2 0d)()(auufua auufua0d)()( 0d)(|)|(auufua auufua0d)(|)|( aattatfd|)|)(二重积分的计算法二重积分的计算法 DDvuJvuyvuxfyxyxfdd),(),(dd),(57二重积分在直角坐标系下的计算二重积分在直角坐标系下的计算二重积分在极坐标系下的计算公式二重积分在极坐标系下的计算公式 (注意使用对称性注意使用对称性)二重积分的计算法二重积分的计算法四、小结四、小结(注意正确选择积分次序注意正确选择积分次序, 掌握交换积分次序掌握交换积分次序的方法的方法)恰当选择坐标系计算二重积分恰当选择坐标系计算二重积分(注意选择的原则注意选择的原则)58思考题思考题11995年考研数学年考研数学(一一)5分分 10,d)(,1 , 0)(Axxfxf并并设设上上连连续续在在设设.d)()(d110yyfxfxx 求求解解 xyyfxxf010d)(d)(令令yyfxfxIxd)()(d1