任意角的三角函数ppt

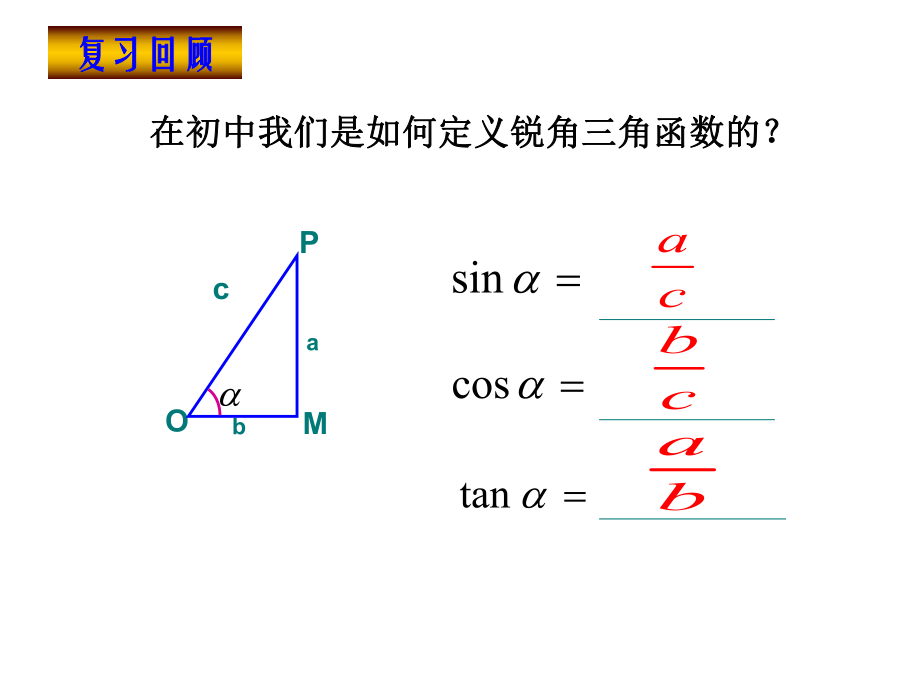
1、5.3任意角的三角函数任意角的三角函数 在初中我们是如何定义锐角三角函数的？在初中我们是如何定义锐角三角函数的？sincostancacbba 复习回顾复习回顾OabMPcOabMP yx 1.在直角坐标系中如何用坐标表示锐角三角函数？在直角坐标系中如何用坐标表示锐角三角函数？新课引入新课引入22:barOPbMPaOM其中 yx 1.在直角坐标系中如何用坐标表示锐角三角函数？在直角坐标系中如何用坐标表示锐角三角函数？raOPOMcosrbOPMPsinabOMMPtanbaP,Mo如果改变点在终边上的位置，这如果改变点在终边上的位置，这三个比值会改变三个比值会改变吗？吗？PMOPMPsinO

2、POMcosOMMPtanOMPPMOPOPMPOOMMOPMMOyxP(a,b)诱思探究诱思探究能否通过能否通过|op|取特殊值将表达式简化呢？取特殊值将表达式简化呢？OPMPsinOPOMcosOMMPtan，则若1 rOPbaab以原点为圆心以原点为圆心, ,以单位以单位长度为半径的圆叫做长度为半径的圆叫做单位圆单位圆. .2.任意角的三角函数定义任意角的三角函数定义 设 是一个任意角，它的终边与单位圆交于点),(yxP 那么:（1） 叫做 的正弦正弦，记作 ，即 ；ysinysin （2） 叫做 的余弦余弦，记作 ，即 ； cosxxcos（3） 叫做 的正切正切，记作 ，即 。 xy

3、tanxytan 所以，正弦，余弦，正切都是所以，正弦，余弦，正切都是以以角为自变量角为自变量，以以单位圆单位圆上点的上点的坐坐标或坐标的比值标或坐标的比值为函数值的函数为函数值的函数，我们将他们统称为我们将他们统称为三角函数三角函数.0 , 1AOyxyxP ,)0(x的终边例例1：如图已知角：如图已知角的终边与单位圆的交点是的终边与单位圆的交点是 求角求角的正弦、余弦和正切值。的正弦、余弦和正切值。)23,21(P解：根据任意角的三角函数定义：23sin21cos3tanOxy)23,21(P点评：若已知角点评：若已知角的终边与单位圆的交点坐标，的终边与单位圆的交点坐标，则可直接利用定义求

4、三角函数值。则可直接利用定义求三角函数值。实例剖析实例剖析例例2 求求 的正弦、余弦和正切值的正弦、余弦和正切值.3535AOB解：在直角坐标系中，作解：在直角坐标系中，作 AOB，易知，易知 的终边与单位圆的交点坐标为的终边与单位圆的交点坐标为 )23,21(所以所以 2335sin2135cos335tanxyoAB35点评：若已知角点评：若已知角的大小求三角函数值时，可先求出角的大小求三角函数值时，可先求出角终边与单位圆的交点，然后再利用定义求三角函数值。终边与单位圆的交点，然后再利用定义求三角函数值。5433换成呢？ yx,P x yMo思考：思考：若点若点P P（x x，y y）为角

5、）为角终边上任意一终边上任意一点，那么点，那么sinsin，coscos，tantan对应的函数对应的函数值分别等于什么？值分别等于什么？sinyrcosxrtanyx22( , )P x yrxy若点到原点的距离为，则例例3:已知角已知角a终边上一点的坐标为终边上一点的坐标为P(-4,-3)，求角求角a的各个三角函数值。的各个三角函数值。解：因为解：因为x=-4，y=-3, 5253422r53sinrya54cosrxa43tanxyaP15 ,8aa练习：已知角 的终边上一点aR且a0 ，sin,cos ,tan求角 的的值.-15 ,8 ,xa ya解：由于22158170raaaa所

6、以 1017 ,ara若则于是88151588sin,cos,tan171717171515aaaaaa 20-17 ,ara若则于是88151588sin,cos,tan171717171515aaaaaa （ ）（ ）（ ）xyosin（ ） （ ）（ ） （ ）xyotan（ ）（ ）（ ）（ ）xyocos探究：探究：三角函数定义域sincostanRR1.三角函数的定义域三角函数的定义域2.三角函数值在各象限的符号三角函数值在各象限的符号|,2kkZ 本节课主要学习了那些内容本节课主要学习了那些内容?任意角三角函数的概念任意角三角函数的概念.归纳总结归纳总结三角函数的定义域及三角函数

7、值在各象限的符号三角函数的定义域及三角函数值在各象限的符号.4P3,sin5_yy 3、若点是角 终边上的一点，且，则sin=_1、角 的终边落在y=-x上，则sintancos=+sincostanxxxyxxx2、函数的值域为（） . 0A . 3B.1C . 3, 1D当堂检测：当堂检测：22D4 例例4 求证：当下列不等式组成立时，求证：当下列不等式组成立时， 角角 为第三象限角为第三象限角.反之也对。反之也对。0tan 0sin 证明：证明： 因为式因为式 成立成立,所以所以 角的终边可能位于第三角的终边可能位于第三 或第四象限，也可能位于或第四象限，也可能位于y 轴的非正半轴上；轴

8、的非正半轴上；0sin 又因为式又因为式 成立，所以角成立，所以角 的终边可能位于的终边可能位于第一或第三象限第一或第三象限. 0tan 因为式都成立，所以角因为式都成立，所以角 的终边只能位于第三象限的终边只能位于第三象限.于是角于是角 为第三象限角为第三象限角.反过来请同学们自己证明反过来请同学们自己证明.终边相同的角的同一三角函数的值是否相等？终边相同的角的同一三角函数的值是否相等？sin( )=sin , 课内练习课内练习2 kcos( )=cos ,2 ktan( )=tan ,2 k利用公式一利用公式一,可以把求任意角的三角函数值可以把求任意角的三角函数值, 转化为求转化为求0到到2 (或或00-3600)角的三角函数值角的三角函数值.(其中其中k )z例例5.确定下列各三角函数值的符号：确定下列各三角函数值的符号： cos250; sin(-/4); sin(-672); cos3;练习练习2. 已知已知sin0且且cos0,确