圆中的最值问题

1、完美WORD格式.整理专业资料分享圆中的最值问题【考题展示】题1 2021年武汉中考在坐标系中,点 A的坐标为3 , 0,点B为y轴正半轴上的一点,点 C是第一象限内一点,且 AC=2设tan / BOC=m贝U m的取值范围是 .题2 2021年武汉元调如图,在边长为1的等边 OAB中,以边AB为直径作O D,以O为圆心OA长为半径作O O, C为半圆弧AB上的一个动点不与A B两点重合,射线AC交O O于点E, BC=a , AC=b,求a b的最大值.有修改题3 2021年武汉四调如图,/ BAC=6C°,半径长为1的圆O与/ BAC的两边相切,P为圆O上一动点,以 P为圆心,

2、PA长为半径的圆P交射线ABAC于DE两点,连接DE那么线段DE长度的最大值为 .题4 2021年武汉五模在厶ABC中,.A =120 , BC =6 .假设 ABC的内切圆半径为 r,贝U r的最大值为.有修改题5 2021年武汉中考如图,E, F是正方形ABCD的边AD上两个动点,满足 AE=DF连接CF交BD于点G,连接BE交AG于点H.假设正方形的边长为 2,那么线段DH长度的最小值是BA题1图BAE题3图D题5图题4图【典题讲练】 类型1 (相关题：题5)1.1如图,边长为a的等边 ABC的顶点A, B分别在x轴正半轴和y轴正半轴上运动,那么动点 C到原点O的 距离的最大值是1.2在

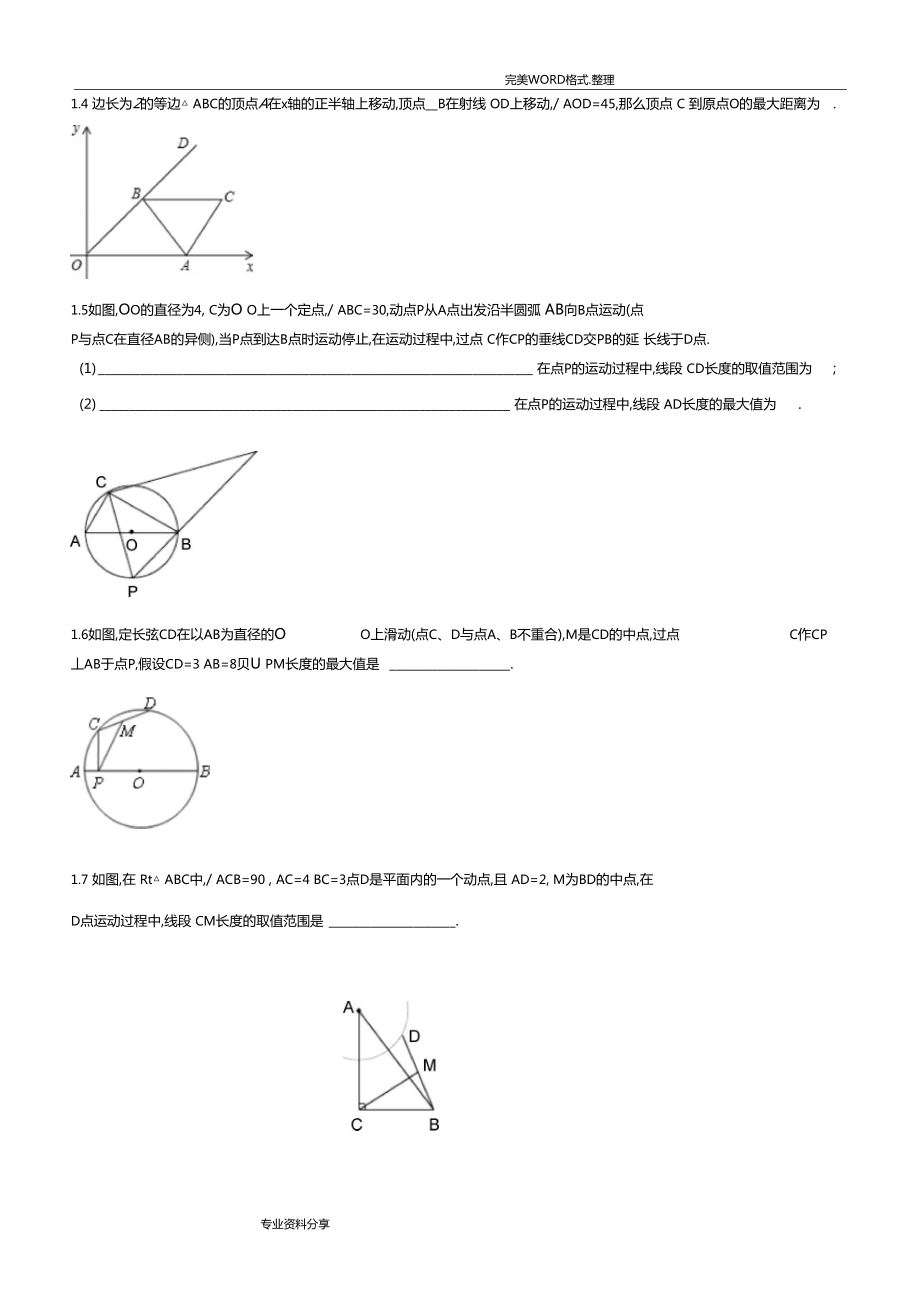
3、直角坐标系中, ABC满足,/ C=90 , AC=8 BC=6,点A, B分别在x轴、y轴上,当A点从原点开始 在正x轴上运动时,点B随着在正y轴上运动(下列图),求原点O到点C的距离OC的最大值,并确定此时图形 应满足什么条件.1.3如图,在平面直角坐标系中, 等腰直角三角形 ABC / C=90 ,AC=BC=2点A、C分别在x轴、y轴上, 当点A从原点开始在x轴的正半轴上运动时,点 C在y轴正半轴上运动.(1) 当A在原点时,求点B的坐标；(2) 当OA=OC寸,求原点 O到点B的距离OB(3) 在运动的过程中,求原点O到点B的距离OB的最大值,并说明理由.1.4 边长为2的等边 AB

4、C的顶点A在x轴的正半轴上移动,顶点_B在射线 OD上移动,/ AOD=45,那么顶点 C 到原点O的最大距离为.1.5如图,OO的直径为4, C为O O上一个定点,/ ABC=30,动点P从A点出发沿半圆弧 AB向B点运动(点 P与点C在直径AB的异侧),当P点到达B点时运动停止,在运动过程中,过点 C作CP的垂线CD交PB的延 长线于D点.(1) 在点P的运动过程中,线段 CD长度的取值范围为 ;(2) 在点P的运动过程中,线段 AD长度的最大值为 .1.6如图,定长弦CD在以AB为直径的OO上滑动(点C、D与点A、B不重合),M是CD的中点,过点C作CP丄AB于点P,假设CD=3 AB=

5、8贝U PM长度的最大值是 .1.7 如图,在 Rt ABC中,/ ACB=90 , AC=4 BC=3点D是平面内的一个动点,且 AD=2, M为BD的中点,在D点运动过程中,线段 CM长度的取值范围是 .类型2 相关题：题42.1如图, AB是O O的弦,C是O O上的一个动点,连接 AC BQ / C=60°,GO的半径为2,那么厶ABC面积的最大值是2.2如图,直线 MN经过O O上的点A,点B在MN上,连OB交O O于C点,且点C是OB的中点,AC= OB2假设点P是O O上的一个动点,当 AB3时, APC的面积的最大值为 2.3如图,半圆 0的半径为1, AC丄AB,

6、BD丄AB且AC=1, BD=3, P是半圆上任意一点,那么封闭图形ABDPC面AB=5,那么斜边上的高的最大值为2.5如图,假设Rt ABC的斜边AB=2内切圆的半径为r,贝U r的最大值为2.6 如图,在 ABC 中,AB=10, AC=8 BC=6 经过点那么线段EF长度的最小值是 .C且与边AB相切的动圆与CB CA分别相交于点E, F,2.7如图,在平面直角坐标系 xOy中,直线AB经过点A(- 4, 0)、B(0,4), OO的半径为1 (O为坐标原点),PQ的最小值为2.8如下图,在直角坐标系中,A点坐标为(-3,- 2) , O A的半径为1, P为x轴上一动点,PQ切O A于

7、类型3 (相关题：题3)3.1如图, ABC中,/ BAC=60,/ABC=45 ,AB=&, D是线段 BC上的一个动点,以 AD为直径画O O分别交AB AC于E, F,连接EF.(1)探究线段EF长度为最小值时,点 D的位置,请画出图形；(2)求出该最小值.3.2 如图,在 ABC中, AB=5 BC=8 AC=7,动点P、Q分别在边AB AC上,使 APQ的外接圆与 BC相切,那么线段PQ的最小值等于类型4 (相关题：题2)4.1如图,点 C在以AB为直径的OO 上,CDLAB于P,设AP=a PB=b.(1)求弦CD的长；(2)如果a+b=1O,求ab的最大值,并求出此时a,

8、 b 的值.(参考 2.4、2.5 )A2 24.2如图,半径为2的OO有两条互相垂直的弦 AB和CD其交点E到圆心O的距离为1,那么AB+CD=D4.3如图,00的半径为2,点P是OO内一点,且0P#5,过P作互相垂直的两条弦 AC BD,那么四边形ABCD 面积的最大值为.A,过A引互相垂直的弦 PQ RS.求PQ+RS取值范围.4.5如图,线段AB=4, C为线段AB上的一个动点, 那么O 0半径的最小值为以AC BC为边作等边 ACD和等边 BCE O 0外接于 CDE匚4.6在平面直角坐标系中,以坐标原点0为圆心,2为半径画O 0, P是O 0上一动点,且P在第一象限内,过点P作O

9、0的切线与x轴相交于点A,与y轴相交于点B,线段AB长度的最小值是类型5 相关题：题15.1如图, A、B两点的坐标分别为-2 , 0、0, 1 , O C的圆心坐标为0,-1,半径为1 , D是O C上的一个动点,射线 AD与y轴交于点 巳那么厶ABE面积的最大值是 .5.2 如图,Rt ABC中,/ C=90°,ZA=30°,AB=4,以AC上的一点 O为圆心OA为半径作O O,假设O O与边BC 始终有交点包括 B、C两点,那么线段AO的取值范围是5.3如图,在 Rt ABC中,/ C=90°,AC=6 BC=8 D为AB边上一点,过点 D作CD的垂线交直线

10、 BC于点E,那么线段CE长度的最小值是5.4在坐标系中,点 A的坐标为3, 0,点B是y轴右侧一点,且 AB=2,点C上直线y=x+1上一动点,且 CB 丄AB于点B,那么tan ACB =m,那么m的取值范围是 .5.5如图,A点的坐标为(-2 , 1),以A为圆心的O A切x轴于点B, P(a, b)为O A上的一个动点,请分别探 索：b亠a的最大值；b亠a的最小值；ba的最大值；ba的最大值；【拓展延伸】：b 2a的范围;类型66.1如图,CD是OO的直径,点A是半圆上的三等分点,CD=4时,求：(1) AP+BP的最小值.(2) AP- BP的最大值.B是弧AD的中点,P点为直线CD

11、上的一个动点,当6.2如图,圆0的面积为3n,AB为直径,弧AC的度数为80°,弧BD的度数为20°,点P为直径AB上任 一点,贝U PC+PD勺最小值为 .6.3如图,AB CD是半径为5的OO的两条弦,AB=8 CD=6 MN是直径,AB丄MN于点E,CDLMN于点F,P 为EF上的任意一点,贝U PA+PQ的最小值为 .完美WORD格式.整理6.4如图,AB是OO的直径,弦BC=2cm F是弦BC的中点,/ ABC=60 .假设动点E以2cm/s的速度从 A点出发 沿着AB方向运动,设运动时间为t (s),连接EF、CE当t为秒时,CE+EF最小,其最小值是 专业资料

12、分享6.5四边形 ABCD内接于圆,/ ADC=90 , CD=4 AC=8 AB=BC设O是AC的中点.(1) 设P是AB上的动点,求 OP+PC勺最小值；(2) 设Q, R分别是AB AD上的动点,求 CQR的周长的最小值.补充练习(与例题类型不完全对应)1.如图,直线I与O O相离,OAL l于点A, OA=5 OA与O O相交于点P, AB与O O相切于点B, BP的延长线交直线I于点C,假设在O O上存在点Q使厶QAC是以AC为底边的等腰三角形,那么O O的半径r的取值范 围为.2.：如图, Rt ABC中,/ B=90o,Z A=30o, BC=6cm点O从A点出发,沿 AB以每秒

13、 Gem的速度向B 点方向运动,当点 O运动了 t秒(t > 0)时,以O点为圆心的圆与边 AC相切于点D,与边AB相交于E、F两 点,过E作EG丄DE交射线BC于 G.(1) 假设点G在线段BC上,贝U t的取值范围是 .(2) 假设点G在线段BC的延长线上,那么t的取值范围是 .3.如图,O M O N的半径分别为 2cm, 4cm,圆心距MN=10cm P为O M上的任意一点,Q为O N上的任意一点, 直线PQ与连心线I所夹的锐角度数为 a,当P、Q在两圆上任意运动时,tanNa的最大值为.4.如图,在矩形 ABCD中, AB=3, BC=4, 0为矩形 ABCD的中央,以 D为圆

14、心1为半径作O D, P为O D上的一 个动点,连接 AP 0P那么厶AOP面积的最大值为 .5.如图,在 Rt ABC中,/ C=90,AC=8 BC=6经过点 C且与边AB相切的动圆与 CA、CB分别相交于点 P、Q,那么线段PQ长度的最小值是.6.如图,在等腰 Rt ABC中,/ C=90°,AC=BC=4 D是AB的中点,点 E在AB边上运动(点 E不与点A重合),过A D、E三点作OO,OO交AC于另一点F,在此运动变化的过程中,线段EF长度的最小值为 .7.如图,A B两点的坐标分别为(2 , 0)、(0, 2) , O C的圆心的坐标为(-1 , 0),半径为1,假设D是O C上的 一个动点,线段 DA与y轴交于点丘,那么厶ABE面积的最小值是 .&如图,等腰 Rt ABC中,/ ACB=90 , AC=BC=4 O C的半径为1,点P在斜边 AB上,PQ切O O于点Q,那么 切线长PQ长度的最小值为 .9.在直角坐标系中,点 A的坐标为(3, 0),点P ( m, n )是第一象限内一点,且 AB=2贝U