理论力学-第五章

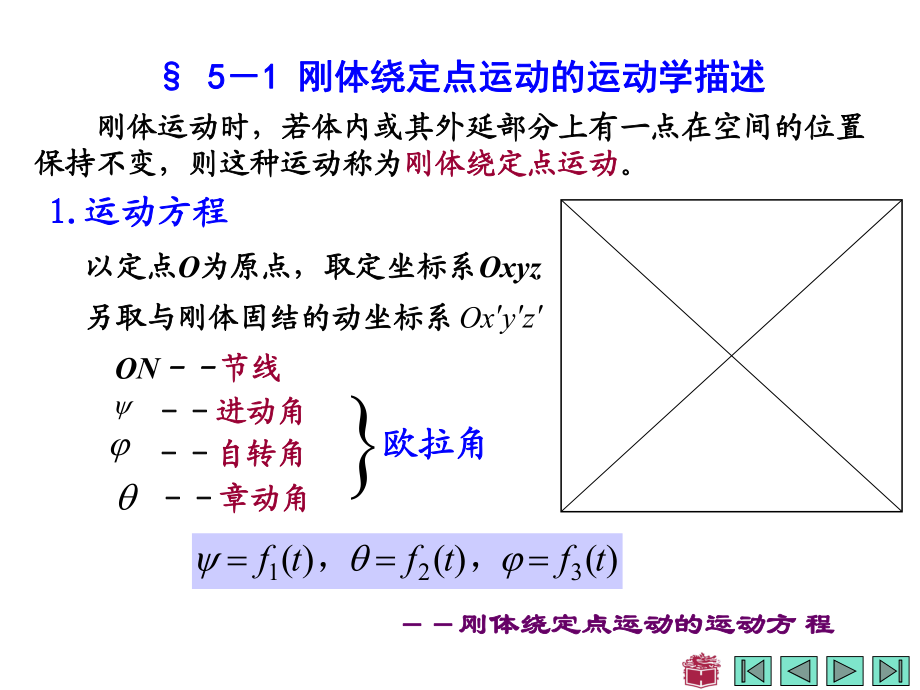
1、圆盘的运动分析 5 51 1 刚体绕定点运动的运动学描述刚体绕定点运动的运动学描述 刚体运动时，若体内或其外延部分上有一点在空间的位置刚体运动时，若体内或其外延部分上有一点在空间的位置 保持不变，则这种运动称为保持不变，则这种运动称为刚体绕定点运动刚体绕定点运动。1.1.运动方程运动方程 以定点以定点O为原点，为原点， 取定坐标系取定坐标系Oxyz 另取与刚体固结的动坐标系另取与刚体固结的动坐标系zyxOON节线节线 进动角进动角 自转角自转角 章动角章动角 欧拉角欧拉角)()()(321tftftf，刚体绕定点运动的运动方刚体绕定点运动的运动方 程程 欧拉角的定义欧拉定理欧拉定理 2.2.欧

2、拉定理欧拉定理 绕定点运动的刚体，从某一位置到另一位置的任何位绕定点运动的刚体，从某一位置到另一位置的任何位 移可以绕通过定点的某一轴转动一次而实现。移可以绕通过定点的某一轴转动一次而实现。证证 明：明： BCABACBACBCABACBACAACBBC3.3.瞬时转动轴瞬时转动轴角速度角速度角加速度角加速度 tt0lim矢量沿瞬轴，矢量沿瞬轴， 指向按右手法则规定指向按右手法则规定 tttddlim0一般情况下一般情况下与与 不共线不共线 方向沿角速度矢量的矢端曲线的切线。方向沿角速度矢量的矢端曲线的切线。 4.4.刚体上各点的速度和加速度刚体上各点的速度和加速度 vrddddddvrart

3、ttarvra1转动加速度转动加速度 大小为大小为2h方向垂直于方向垂直于 和和r指向如上图。指向如上图。2av向轴加速度向轴加速度 其大小为其大小为12h方向垂直于方向垂直于 和和v指向瞬轴。指向瞬轴。 刚体绕定点运动时，刚体内任一点的速度等于绕瞬轴刚体绕定点运动时，刚体内任一点的速度等于绕瞬轴 转动的角速度与矢径的矢量积；该点的加速度等于绕瞬轴转动的角速度与矢径的矢量积；该点的加速度等于绕瞬轴的向轴加速度与绕角加速度矢的转动加速度的矢量和。的向轴加速度与绕角加速度矢的转动加速度的矢量和。例例 5 51 1求：齿轮上点求：齿轮上点M 的速度和加速度。的速度和加速度。 设设 OA=l， 已知：

4、行星锥齿轮的轴已知：行星锥齿轮的轴OA以匀角速度以匀角速度 , ,绕铅直轴绕铅直轴OB 转动转动 1AC=r。解：解： 齿轮中心点齿轮中心点A 的速度为的速度为 sinAvOA 点点A 绕定点绕定点O 在水平面内作圆周运动在水平面内作圆周运动 1AvOA绕瞬轴绕瞬轴OC 转动的角速度的大小为转动的角速度的大小为 sin1= =常量常量 它沿着它沿着OC 指向如图所示指向如图所示 点点M 的速度为的速度为 1112 cos2 sin2sinsinMvMErll它的方向垂直于平面它的方向垂直于平面 OMC 指向如图指向如图 行星齿轮的角速度为行星齿轮的角速度为 ddt因为因为 只改变方向不改变大小

5、只改变方向不改变大小 而且它和而且它和z z 轴间夹角轴间夹角的大小保的大小保 持不变，所以它的矢端曲线是持不变，所以它的矢端曲线是水平的圆周。水平的圆周。1ddt沿此圆周的切线，沿此圆周的切线， 指向指向 转动的一转动的一 方方 1的大小为的大小为cotcossinsin21111现在计算点现在计算点M的加速度。的加速度。 转动加速度转动加速度 的大小的大小 为为 1a21211sincoscotllOMa它垂直由它垂直由 和和OM 形成的平面，形成的平面， 指向如图指向如图 向轴加速度向轴加速度 的大小为的大小为 2a21222sin2sin2llMEa它的方向自它的方向自M 指向点指向点

6、E（在铅直平面（在铅直平面OAC 内）内） 21aaa2cos22122212aaaaa将将 值代入上式，值代入上式， 21aa 、并注意到并注意到 22sincotlrrrl和和得得221)(9rlla 5 52 2 自由刚体的运动自由刚体的运动)()()()()()(654321tftftftfztfytfxOOO，自由刚体运动方程自由刚体运动方程 自由刚体内任一点自由刚体内任一点M 的速度的速度 aervvvOv设动点设动点M M 在动坐标系在动坐标系 中的矢径为中的矢径为Or刚体绕基点刚体绕基点 转动的瞬时角速度为转动的瞬时角速度为Or则则vrrr自由刚体内自由刚体内任一点的速度公式任

7、一点的速度公式为为 MOvvrr由于牵连运动为平移，由于牵连运动为平移， 自由刚体内任一点的加速度合成式为自由刚体内任一点的加速度合成式为 reaaaa其中其中Oaaerrrrraara为刚体绕基点为刚体绕基点 转动的瞬时角加速度转动的瞬时角加速度 O自由刚体内自由刚体内任一点的加速度公式任一点的加速度公式为为 rr2r121araaaaaaOM， 5 53 3 刚体运动的合成刚体运动的合成刚体的任何复杂运动都可以由几个简单运动的合成而得到。刚体的任何复杂运动都可以由几个简单运动的合成而得到。 1.1.平移与平移的合成平移与平移的合成 小车上任一点的速度：小车上任一点的速度： 21vvvvve

8、r12reaaaaa当刚体同时作两个平移时，刚体的合成运动仍为平移。当刚体同时作两个平移时，刚体的合成运动仍为平移。 加速度：加速度： 2.2.绕两个平行轴转动的合成绕两个平行轴转动的合成 齿轮齿轮IIII上任一点上任一点M 的速度的速度 Mv牵连速度的大小为牵连速度的大小为 Mrvvvee1eMO方向垂直于方向垂直于MO1相对速度的大小为相对速度的大小为 2vO Mrr方向垂直于方向垂直于MO2这时点这时点M 的速度等于的速度等于 与与 的矢量和。的矢量和。vevr瞬轴与两轴间的距离分别为瞬轴与两轴间的距离分别为 和和CO1CO2在点在点C reCOCO2r1eer21COCO与与 同向的情

9、形如图同向的情形如图 er2122OvOOO Cea齿轮绕瞬轴转动的角速度为齿轮绕瞬轴转动的角速度为 21222OvOOO CO CaeCOCOOO2121era方向根据方向根据 的方向确定的方向确定 2O 当刚体同时绕两平行轴同向转动时，刚体的合成运动当刚体同时绕两平行轴同向转动时，刚体的合成运动 为绕瞬轴的转动，绝对角速度等于牵连角速度与相对角速为绕瞬轴的转动，绝对角速度等于牵连角速度与相对角速度的和；瞬轴的位置内分两轴间的距离，内分比与两个角度的和；瞬轴的位置内分两轴间的距离，内分比与两个角速度成反比。速度成反比。当当 和和 反向时如图反向时如图erCOCOOO2121rea绝对角速度的

10、转向，绝对角速度的转向，与与 中较大的一个相同。中较大的一个相同。 er 当刚体同时绕两平行轴反向转动，当刚体同时绕两平行轴反向转动， 刚体的合成运动为绕瞬轴的转动，绝对刚体的合成运动为绕瞬轴的转动，绝对 角速度等于牵连角速度与相对加速度之角速度等于牵连角速度与相对加速度之 差，它的转向与较大的角速度的转向相差，它的转向与较大的角速度的转向相同；瞬轴的位置外分两轴间的距离，在同；瞬轴的位置外分两轴间的距离，在较大角速度的轴的外侧，外分与两个角较大角速度的轴的外侧，外分与两个角速度成反比。速度成反比。当当 和和 等值而反向时等值而反向时er0a 当刚体以同样大小的角速度，同时绕两平行轴而反向转当

11、刚体以同样大小的角速度，同时绕两平行轴而反向转 动时，刚体的合成运动为平移，这种运动称为动时，刚体的合成运动为平移，这种运动称为转动偶转动偶。转动偶3.3.绕相交轴转动的合成绕相交轴转动的合成 er1 12222COCBOACvvvhhAAOACOCBAA点点C 的绝对速度等于零。的绝对速度等于零。 直线直线OC 是刚体的瞬轴。是刚体的瞬轴。 ADA1AEAa1aAEADOACBOACBAAEOCAAD，11AEADOCOCa角速度角速度 的指向可由点的指向可由点A A 的速度方向确定。的速度方向确定。 a21a 当刚体同时绕两相交轴转动时，合成运动为绕瞬轴的转动，当刚体同时绕两相交轴转动时，

12、合成运动为绕瞬轴的转动， 绕瞬轴转动的角速度等于绕两轴转动的角速度的矢量和。绕瞬轴转动的角速度等于绕两轴转动的角速度的矢量和。如果刚体绕相交于一点的如果刚体绕相交于一点的3 3个轴或更多的轴转动时个轴或更多的轴转动时 niin121 当刚体同时绕相交于一点的多轴转动时，合成运动为绕当刚体同时绕相交于一点的多轴转动时，合成运动为绕 瞬轴的转动。绕瞬轴转动的角速度等于绕各轴转动的角速度瞬轴的转动。绕瞬轴转动的角速度等于绕各轴转动的角速度的矢量和，而瞬轴则沿此合矢量方向。的矢量和，而瞬轴则沿此合矢量方向。4.4.平移与转动的合成平移与转动的合成 （1 1）平移速度矢与转动角速度矢垂直的情形）平移速度

13、矢与转动角速度矢垂直的情形 OvO C绕瞬轴转动的角速度绕瞬轴转动的角速度a等于绕动轴等于绕动轴 转动的角速度转动的角速度zO （2 2）平移速度矢与转动角速度矢平行的情形）平移速度矢与转动角速度矢平行的情形 刚体绕轴刚体绕轴 转动，同时又沿轴向运动转动，同时又沿轴向运动 螺旋运动。螺旋运动。zO 平移速度与转动角速度的比值平移速度与转动角速度的比值 螺旋率。螺旋率。Ovp若以若以s表示刚体沿轴表示刚体沿轴 的轴向位移的轴向位移 zO 为刚体绕轴为刚体绕轴 的转角的转角 zO ddddOsvtt，螺旋率可写成螺旋率可写成 ddsp 一般情况下，螺旋率为一恒值，上式积分一次：一般情况下，螺旋率为

14、一恒值，上式积分一次： ps 2sp2s s表示刚体转过一周沿轴前进的距离表示刚体转过一周沿轴前进的距离螺距螺距。 （3 3）平移速度矢与转动角速度矢成任意角的情形）平移速度矢与转动角速度矢成任意角的情形 刚体以角速度刚体以角速度 绕动轴绕动轴 转动，转动，zO 同时又以速度同时又以速度 平移，平移，OvOv和和 之间的夹角为之间的夹角为 。 刚体的运动成为以刚体的运动成为以 的平移，和以的平移，和以 绕瞬轴绕瞬轴CC 的转动的转动 的合成运动的合成运动瞬时螺旋运动瞬时螺旋运动。2v例例 5 52 2已知：如图所示，系杆已知：如图所示，系杆 以角速度以角速度 绕轴绕轴 转动，半径转动，半径 为

15、为 的行星齿轮活动地套在与系杆一端固结的轴的行星齿轮活动地套在与系杆一端固结的轴 上，上， 并与半径为并与半径为 的固定齿轮相啮合。的固定齿轮相啮合。21OOe1O2r2O1r求：行星齿轮的绝对角速度求：行星齿轮的绝对角速度 。 2以及它相对于系杆的角速度以及它相对于系杆的角速度 。 r解：解：er21rr行星齿轮相对于系杆的角速度为行星齿轮相对于系杆的角速度为 e21rrr行星齿轮的绝对角速度为行星齿轮的绝对角速度为 e21er2)1 (rr2 2、以逆时针为正以逆时针为正 1 1、211r2rrrre2re2r1e10，r2rer1e21rrre212)1 (rr例例 5 53 3已知：行

16、星齿轮已知：行星齿轮IIII与固定锥齿轮与固定锥齿轮I I相啮合，可绕动轴相啮合，可绕动轴 转动，而动轴以角速度转动，而动轴以角速度 绕定轴绕定轴 转动。设在点转动。设在点C 处轮处轮I I的半径为的半径为 ，轮，轮IIII的半径为的半径为 。 2OOe1OO1r2r求：锥齿轮求：锥齿轮IIII相对于动轴的角速度相对于动轴的角速度 。 r解：解：1e2rOOOOe21e12rrrOOOO2 2、研究齿轮研究齿轮I I和和IIII相对于动轴相对于动轴 的运动的运动2OO如图所示如图所示 两齿轮相对于动轴两齿轮相对于动轴 的角速度分别为的角速度分别为 和和2OO1r2r传动比传动比211rr2rr

17、将将 代入上式代入上式r21r得得e21rr2rr1 1、例例 5 54 4已知：框架已知：框架K和轴和轴A一起以角速度一起以角速度绕轴绕轴I IIIII转动，半径转动，半径 为为 和和 彼此相固结的两个伞齿轮彼此相固结的两个伞齿轮B和和C 可在轴可在轴 A上自由转动。伞齿轮上自由转动。伞齿轮B与轴与轴I I上半径为上半径为 的伞齿轮的伞齿轮 D 相啮合，伞齿轮相啮合，伞齿轮C与轴与轴IIII上半径为上半径为 的伞齿轮的伞齿轮E相相 啮合。轴啮合。轴I I的角速度的角速度 和轴和轴IIII的角速度的角速度 。1r2r1R2RIII求：框架的角速度求：框架的角速度和齿轮和齿轮B相对于框架的角速度

18、相对于框架的角速度 。 Br解：解：IIIIrIIr，齿轮的传动关系如下齿轮的传动关系如下 22BrIIr11BrIrRrRr，和和 中必定有一个的转向与图示的转向相反中必定有一个的转向与图示的转向相反 IIrBr1221IIIRrRr2112II21I12RrRrRrRr)(I11Ir11BrrRrR)(III211221BrRrRrRR例例 5 55 5求：求：t=1s时陀螺绕瞬轴转动的角速度。时陀螺绕瞬轴转动的角速度。 已知：陀螺绕定点运动时，如图所示已知：陀螺绕定点运动时，如图所示3 3个欧拉角表示的运动个欧拉角表示的运动 方程为方程为式中式中223246ttt，t以以s s计计 以以

19、rad计计，解：解：24034t，当当t t=1s=1s时时2407，a因为因为0rad/s27.30cos222a 332123)180sin(arcsinattt246322， 5 54 4 陀螺仪近似理论陀螺仪近似理论陀螺现象陀螺现象 工程中把具有一个固定点，并绕自身的工程中把具有一个固定点，并绕自身的 对称轴高速转动的刚体对称轴高速转动的刚体陀螺陀螺。设陀螺以设陀螺以 绕对称轴绕对称轴 转动转动zO 轴又以角速度轴又以角速度 绕定轴绕定轴Oz 转动转动ezO ea)e(ddOOMtL自转自转进动进动在一般情况下，在一般情况下，与自转轴与自转轴 不重合。不重合。) e (OOML，zO

20、其中其中 是陀螺对于对称轴是陀螺对于对称轴 的转动惯量的转动惯量zJzO 动量矩矢近似与对称轴动量矩矢近似与对称轴 重合重合zO 其大小等于其大小等于zJtLuOdd)e(OMu质点系动量定理的运动学解释质点系动量定理的运动学解释 赖柴定理赖柴定理质点系对某定点的动量矩矢端的速度等于外力对同一点的主矩。质点系对某定点的动量矩矢端的速度等于外力对同一点的主矩。 zOJL)e(ddOOMtL1.1.自由陀螺保持自身对称轴在惯性参考系中的方位不变自由陀螺保持自身对称轴在惯性参考系中的方位不变 不计摩擦，外力对其质心不计摩擦，外力对其质心O 的力矩为零的力矩为零 自由陀螺自由陀螺0dd0)e(tLMO

21、O，OL恒量恒量2.2.陀螺受力矩的作用，当力矩矢与对称轴不重合，对称轴将进动陀螺受力矩的作用，当力矩矢与对称轴不重合，对称轴将进动 )(PMuO根据赖柴定理根据赖柴定理在重力在重力 的持续作用下，的持续作用下，P对称轴对称轴 将绕将绕Oz 转动转动 zO 这种运动称为进动这种运动称为进动 zOJLuee)e(eOzMJsin)e(ezOJM3.3.陀螺效应和陀螺力矩陀螺效应和陀螺力矩 陀螺效应陀螺效应是在高速转动的机械中，当转子的对称轴的方是在高速转动的机械中，当转子的对称轴的方 位改变时发生的一种物理现象。位改变时发生的一种物理现象。它的动量矩矢它的动量矩矢zJL 方向沿此对称轴。方向沿此对称轴。 如果轴如果轴z z以角速度以角速度 绕轴绕轴y y转动转动e则动量矩矢端点则动量矩矢端点A A获得速度获得速度uLuezeOJuMe)(e)(gzeOJMMgM陀螺力