运筹学 第一讲.

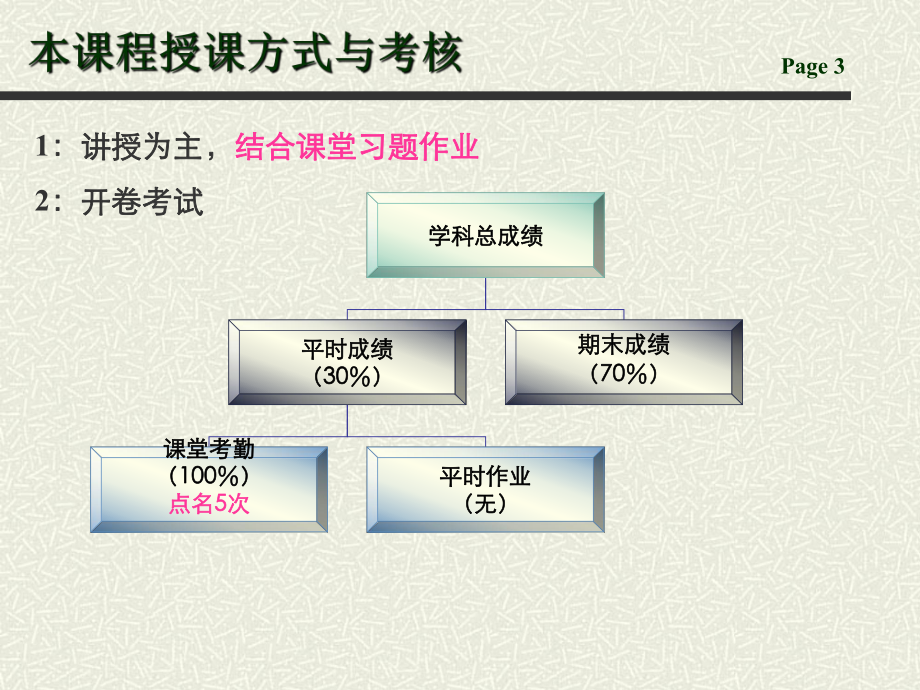
1、运运 筹筹 学学( Operations Research )邹邹 江江Page 2选用教材选用教材 运筹学运筹学 运筹学教材编写组运筹学教材编写组 清华大学出版社清华大学出版社参考教材参考教材运筹学教程运筹学教程胡运权主编胡运权主编 第四版第四版 清华大学出版社清华大学出版社刊物刊物 MManagement science Interfaces European Journal of Operations Research 运筹与管理运筹与管理Page 3学科总成绩学科总成绩平时成绩平时成绩（3030）课堂考勤课堂考勤（100100）点名点名5 5次次平时作业平时作业（无）（无）期末成绩期末

2、成绩（7070）1：讲授为主，：讲授为主，结合课堂习题作业结合课堂习题作业2：开卷考试：开卷考试（1）运筹学简述）运筹学简述（2）运筹学的主要分支）运筹学的主要分支（3）本课程的特点及学习方法）本课程的特点及学习方法（4）运筹学在工商管理、工程管理、物流管理中）运筹学在工商管理、工程管理、物流管理中 的应用的应用本章主要内容：本章主要内容：Page 5一一:运筹学的概念运筹学的概念 目前并没有一个统一的概念。目前并没有一个统一的概念。1：译为：译为“运作研究运作研究”。运筹学是运用科学的方法来决定如何最。运筹学是运用科学的方法来决定如何最佳地运营和设计各种系统的一门学科。佳地运营和设计各种系统

3、的一门学科。2：在美国有人把运筹学称之为管理科学：在美国有人把运筹学称之为管理科学(Management Science)。3：“依照给定条件和目标，从众多方案中选择最佳方案依照给定条件和目标，从众多方案中选择最佳方案”故又名故又名最优化理论最优化理论（现代最优化理论现代最优化理论）。因其有统筹优化的含义，）。因其有统筹优化的含义，借鉴史记借鉴史记“运筹于帷幄之中，决胜于千里之外运筹于帷幄之中，决胜于千里之外”，我国取名为运，我国取名为运筹学。筹学。Page 64：在分析研究问题的基础上，建立数学模型描来述所研究：在分析研究问题的基础上，建立数学模型描来述所研究的问题，求解并检验该模型，从而得

4、出最优解，用于指导现的问题，求解并检验该模型，从而得出最优解，用于指导现实问题的决策。（实问题的决策。（补充补充）真实系统真实系统系统分析系统分析问题描述问题描述模型建立模型建立与修改与修改模型求解模型求解与检验与检验结果分析与结果分析与实施实施数据准备数据准备Page 7 产品甲产品乙设备能力（h）设备A3 32 26565设备B2 21 14040设备C0 03 37575利润（元/件）1500150025002500 Page 8目标函数目标函数 Max z =1500 x1+2500 x2 约束条件约束条件 s.t. 3x1 + 2x2 65 2x1 + x2 40 3x2 75 x1

5、 ,x2 0 Page 9运筹学的历史（略）运筹学的历史（略）1：运筹学思想的出现可以追溯到很早：运筹学思想的出现可以追溯到很早“田忌赛马田忌赛马”、孙子兵法孙子兵法等都体现了博弈论的等都体现了博弈论的思想思想2：第二次世界大战期间：第二次世界大战期间 美、英等国家的作战美、英等国家的作战研究小组解决作战中所遇到的许多错综复杂的战略、研究小组解决作战中所遇到的许多错综复杂的战略、战术问题而对运筹学做了进一步的研究。战术问题而对运筹学做了进一步的研究。3：1947年，丹齐格在研究美国空军配置时，提出年，丹齐格在研究美国空军配置时，提出了求解了求解线性规划问题线性规划问题的的单纯型法（里程碑式的发

6、现单纯型法（里程碑式的发现解决了算法的问题，使得运筹学得到飞速的发展）解决了算法的问题，使得运筹学得到飞速的发展）4：康托洛维奇康托洛维奇最佳资源利用的经济计算最佳资源利用的经济计算Page 10规划问题（规划问题（线性规划线性规划、非线性规划、非线性规划、整数规整数规划、多目标规划划、多目标规划、动态规划等）、动态规划等）图论（图论（横道图、双代号网络图、最短路、最大流横道图、双代号网络图、最短路、最大流）和工程管理中的进度控制结合尤其紧密和工程管理中的进度控制结合尤其紧密库存论（库存论（econimic order quantity和和newsvendors problem）排队论（随机理

7、论）排队论（随机理论）对策论（对策论（game theroy）排序与统筹方法排序与统筹方法决策分析（决策论）决策分析（决策论）Page 11先修课：先修课：高等数学，概率论与数理统计、线性代数高等数学，概率论与数理统计、线性代数特点：特点： 应用数学、交叉科学应用数学、交叉科学 系统整体优化系统整体优化 模型方法的应用，以定量研究为主，定性研模型方法的应用，以定量研究为主，定性研究为辅究为辅 （运筹学、博弈论、计量经济学）（运筹学、博弈论、计量经济学）Page 12学习方法建议：学习方法建议： 数学建模能力的培养数学建模能力的培养+模型求解能力的训练模型求解能力的训练Page 13运筹学在工商

8、管理、工程管理、物流管理中的应用涉及几个运筹学在工商管理、工程管理、物流管理中的应用涉及几个方面：方面：l 生产计划安排生产计划安排l 运输问题运输问题l 人事管理人事管理l 库存管理库存管理l 市场营销市场营销l 财务和会计财务和会计其他，还应用于设备维修、更新和可靠性分析，项目的选择其他，还应用于设备维修、更新和可靠性分析，项目的选择与评价，工程优化设计等。与评价，工程优化设计等。Page 14Interface上发表的部分获奖项目上发表的部分获奖项目组织组织应用应用效果效果联合航空公司联合航空公司在满足乘客需求的前提下，以最低成在满足乘客需求的前提下，以最低成本进行订票及机场工作班次安排

9、本进行订票及机场工作班次安排每年节约成本每年节约成本600600万美元万美元CitgoCitgo石油公司石油公司优化炼油程序及产品供应、配送和营优化炼油程序及产品供应、配送和营销销每年节约成本每年节约成本70007000万万AT&TAT&T优化商业用户的电话销售中心选址优化商业用户的电话销售中心选址每年节约成本每年节约成本4.064.06亿美元，亿美元，销售额大幅增加销售额大幅增加标准品牌公司标准品牌公司控制成本库存（制定最优再定购点和控制成本库存（制定最优再定购点和定购量确保安全库存）定购量确保安全库存）每年节约成本每年节约成本380380万美元万美元法国国家铁路公司法国国家

10、铁路公司制定最优铁路时刻表并调整铁路日运制定最优铁路时刻表并调整铁路日运营量营量每年节约成本每年节约成本15001500万美元，万美元，年收入大幅增加。年收入大幅增加。Taco BellTaco Bell优化员工安排，以最低成本服务客户优化员工安排，以最低成本服务客户每年节约成本每年节约成本13001300万美元万美元DeltaDelta航空公司航空公司优化配置上千个国内航线航班来实现优化配置上千个国内航线航班来实现利润最大化利润最大化每年节约成本每年节约成本1 1亿美元亿美元Page 15例：例： 某工厂拥有某工厂拥有A A、B B、C C 三种类型的设备，生产甲、乙两种产三种类型的设备，生

11、产甲、乙两种产品。每件产品在生产中需要占用的设备机时数，每件产品可品。每件产品在生产中需要占用的设备机时数，每件产品可以获得的利润以及三种设备可利用的时数如下表所示以获得的利润以及三种设备可利用的时数如下表所示 产品甲产品乙设备能力（h）设备A3 32 26565设备B2 21 14040设备C0 03 37575利润（元/件）1500150025002500 Page 16问题：问题： 工厂应如何安排生产可获得最大的总利润？工厂应如何安排生产可获得最大的总利润？解：设变量解：设变量xi为第为第i种（甲、乙）产品的生产件数（种（甲、乙）产品的生产件数（i1 1，2 2）。根据前面分析，可以建立

12、如下的线性规划模型：）。根据前面分析，可以建立如下的线性规划模型： Max z = 1500 x1 + 2500 x2 s.t. 3x1+ 2x2 65 2x1+ x2 40 3x2 75 x1 , x2 0 Page 17例：某公司从两个产地例：某公司从两个产地A1、A2将物品运往三个销地将物品运往三个销地B1、B2、B3，各产地的产量、各销地的销量和各产地运往各销地每，各产地的产量、各销地的销量和各产地运往各销地每件物品的运费如下表所示，问：应如何调运可使总运输费用件物品的运费如下表所示，问：应如何调运可使总运输费用最小？最小？ B1 B2 B3 产量产量 A1 6 4 6 200 A2

13、6 5 5 300 销量销量 150 150 200 Page 18解：设解：设 xijxij 为从产地为从产地AiAi运往销地运往销地BjBj的运输量，的运输量，得到下列运输量表得到下列运输量表 B1 B2 B3 产量产量 A1 x11 x12 x13 200 A2 x21 x22 x23 300 销量销量 150 150 200 Page 19 Min f = 6x11+4x12+6x13+6x21+5x22+5x23 s.t. x11+ x12 + x13 = 200 x21 + x22+ x23 = 300 x11 + x21 = 150 x12 + x22 = 150 x13 + x

14、23 = 200 xij0(i=1,2；j=1,2,3）Page 20 经典报童模型是描述零售商的经典报童模型是描述零售商的两难决策两难决策行为的模型。零售行为的模型。零售商所面临的是随机需求，当零售商订购量大于顾客的需求商所面临的是随机需求，当零售商订购量大于顾客的需求时，会剩余一部分产品。这部分剩余的产品会带来相应的时，会剩余一部分产品。这部分剩余的产品会带来相应的管理费用以及还具有一定的残值，而当零售商订购量小于管理费用以及还具有一定的残值，而当零售商订购量小于顾客需求量时，会由于订货量不足而产生缺货损失顾客需求量时，会由于订货量不足而产生缺货损失Page 21x-零售商所面临的随机需求

15、；f(x)-随机需求的概率密度函数；F(X)-随机需求的累积分布函数；P-产品单位销售价格；W-产品单位购买价格；V-产品残值；S-产品缺货损失；q-订货量；Cs-供应商产品生产成本。Page 22零售商利润函数为：零售商利润函数为：零售商期望利润函数为min,max,0max,0rPx qVqxSxqWq 000min,max,0max,0rEPx q f x dxVqxf x dxSxqf x dxWq1PSWqFPSVPage 23 下料问题下料问题例：现有一批某种型号的圆钢长例：现有一批某种型号的圆钢长8米，需要截取米，需要截取2.5米米长的毛坯长的毛坯100根，长根，长1.3米的毛坯

16、米的毛坯200根。问如何才能根。问如何才能既满足需要，又能使总的用料最少？既满足需要，又能使总的用料最少？解：为了找到一个省料的套裁方案，必须先设计出较好的几解：为了找到一个省料的套裁方案，必须先设计出较好的几个下料方案。其次要求这些方案的总体能裁下所有各种规格个下料方案。其次要求这些方案的总体能裁下所有各种规格的圆钢，以满足对各种不同规格圆钢的需要并达到省料的目的圆钢，以满足对各种不同规格圆钢的需要并达到省料的目的，为此可以设计出的，为此可以设计出4种下料方案以裁用种下料方案以裁用2.5m32101.3m0246料头料头0.2Page 24 )(0200642

17、10023min4323214321jxxxxxxxxxxxZj设按方案设按方案、下料的原材料根数分别为下料的原材料根数分别为xj (j=1，2,3,4)，可列出下面的数学模型：，可列出下面的数学模型：Page 25例例 某办公楼工程，建筑面积某办公楼工程，建筑面积5500m，框架结构，独立柱基，框架结构，独立柱基础，上设承台梁，独立柱基础埋深为础，上设承台梁，独立柱基础埋深为1.5m，地质勘察报告，地质勘察报告中地基基础持力层为中砂层，基础施工钢材由建设单位供应。中地基基础持力层为中砂层，基础施工钢材由建设单位供应。基础工程施工分为两个施工流水段，组织流水施工，根据工基础工程施工分为两个施工流水段，组织流水施工，根据工期要求编制了工程基础项目的施工进度计划，并绘出施工双期要求编制了工程基础项目的施工进度计划，并绘出施工双代号网络计划图，如下图所示：代号网络计划图，如下图所示：Page 26Page 27在工程施工中发生如下事件：在工程施工中发生如下事件：事件一：土方事件一：土方2施工中，开挖后发现局部基础地基持力层为软弱层需处施工中，开挖后发现局部基础地基持力层为软弱层需处理，工期延误理，工期延误6天。天。事件二：承台梁