2021-2022学年北师大版八年级数学上册第一章1

1、2021-2022学年度山东省滕州市鲍沟中学第一学期数学课时训练 八年级数学第一章1.2 一定是直角三角形吗一、单选题1 .我国汉代的赵爽在注释周髀算经时给出了勾股定理的无字证明，人们称它为“赵爽弦图”，“赵爽弦图”指的是（）2.小明想知道学校旗杆的高度， 他发现旗杆上的绳子垂到地面还多 2米，当他把绳子的下端拉开6米后,发现下端刚好接触地面，则旗杆的高度是（）A. 6 米B. 8 米C 10 米D. 12 米6.勾股定理是历史上第一个把数与形联系起来的定理，其证明是论证几何的发端.下面四幅图中不能证明勾股定理的是（）7 .在西方，人们称为毕达哥拉斯定理，在我国把它称为勾股定理，其具体内容指的

2、是（）A.如果直角三角形的两条直角边分别为a, b,斜边为c,那么a2+b2=c28 .如果直角三角形的三边分别为 a, b, c,那么a2+b2=c2C.如果三角形的三边分别为 a, b, c,那么a2+b2=c2D.如果三角形的三边长 a, b, c满足a2+b2=c2,那么这个三角形是直角三角形1,以直角三角8 .勾股定理是人类最伟大的科学发现之一，在我国古算书（周髀算经）中早有记载；如图形的各边为边分别向外作正方形，再把较小的两张正方形纸片按图2的方式放置在最大正方形内若直角三角形两直角边分别为6和8,则图中阴影部分的面积为（）C. 28D.无法求出9 .我国古代数学著作九章算术中记载

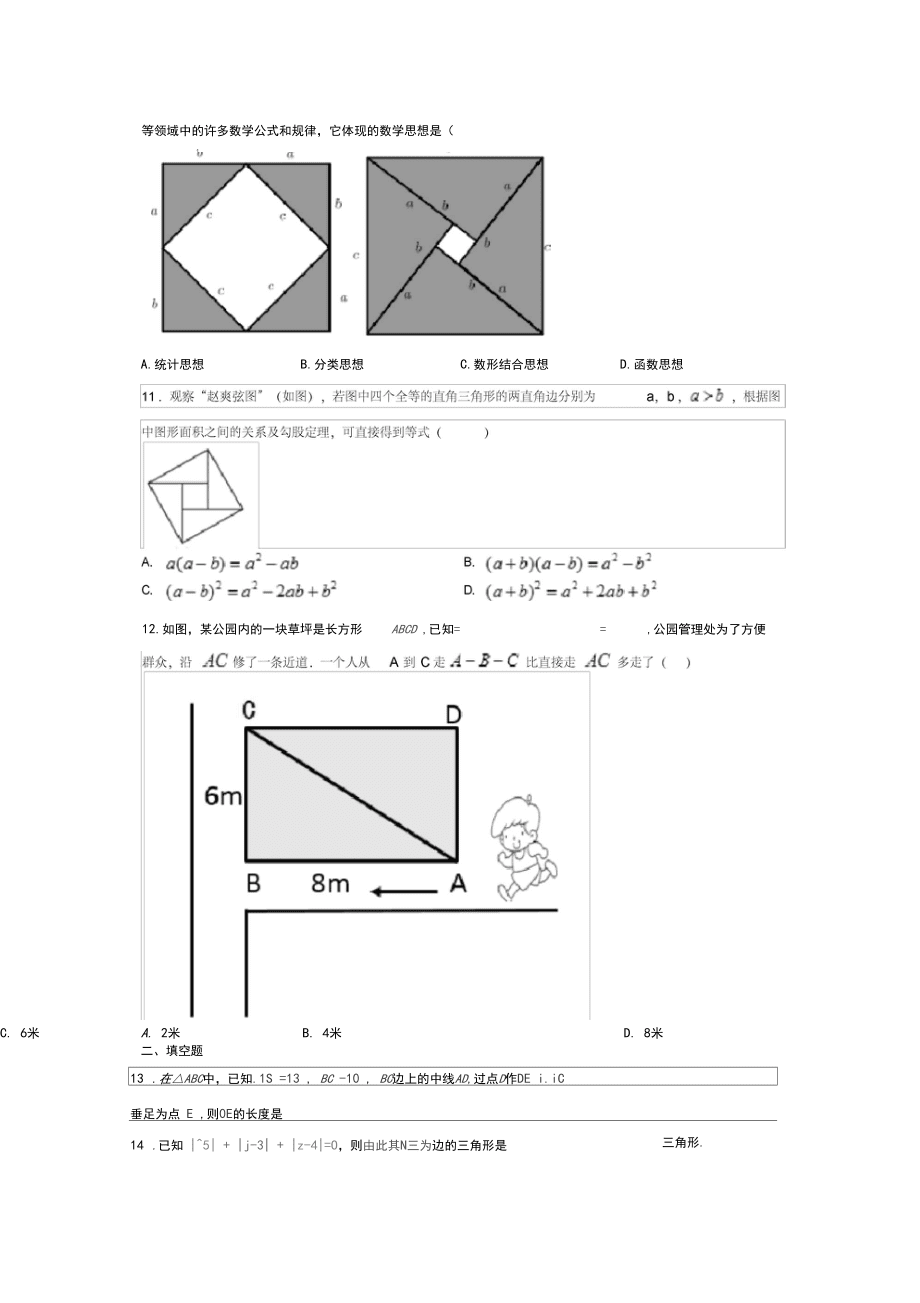
3、了一个问题：“今有池方一丈，葭（ ji 4）生其中，出水一尺，引葭赴岸，适与岸齐.间水深几何.”（丈、尺是长度单位，1丈=10尺，）其大意为：有一个水池，水面是一个边长为10尺的正方形，在水池正中央有一根芦苇，它高出水面1尺.如果把这根芦苇拉向水池一边的中点，它的顶端恰好到达池边的水面，水的深度是多少？则水深为（）A. 10 尺B. 11 尺C. 12 尺D. 13 尺10 .在勾股定理的学习过程中，我们已经学会了运用以下图形，验证著名的勾股定理：这种根据图形直观推论或验证数学规律和公式的方法，简称为“无字证明”.实际上它也可用于验证数与代数，图形与几何等领域中的许多数学公式和规律，它体现的数

4、学思想是（）1A.统计思想B.分类思想C.数形结合思想D.函数思想12.如图，某公园内的一块草坪是长方形ABCD ,已知=,公园管理处为了方便B. 4米C. 6米D. 8米A. 2米二、填空题13 .在ABC中，已知.1S =13 , BC -10 , BC边上的中线AD,过点D作DE i.iC垂足为点 E ,则0E的长度是三角形.14 .已知 |5| + |j-3| + |z-4|=O，则由此其N三为边的三角形是15 .如果线段 a 瓦t能组成一个直角三角形， 那么巴.一，£组成直角三角形.（填“能”或“不3 T - 1Jar *1 ir能”）.16.我国古代数学著作九章算术中的一

5、个问题，如图，一根竹子高一丈，折断后竹子顶端落在离竹子底端3尺处，折断处离地面的高度是 （其中的丈，尺是长度单位，1丈=10尺）.17.如图，在心，3c中，=则三个半圆面积S1, S2, S3的关系为18 .用4张全等的直角三角形纸片拼接成如图所示的图案，得到两个大小不同的正方形.若正方形ABCD的面积为10, AH = 3,则正方形EFGH的面积为:19 .如图，是我国古代数学家赵爽用来证明勾股定理的著名的“赵爽弦图”，其中、nBCG、CDF和口是四个全等的直角三角形，四边形 ABCD和EFGH都是正方形，根据这个图形的面积关系，可以证明勾股定理，设 AD=c , aE = 口, DE =右

6、，取c = 0 , 口一S = 2 .则 3" =20 .九章算术中有一道题：“今有竹高一丈，末折抵地，去本三尺，问折者高几何？”大致意思是：一根竹子高1丈，折断后竹子顶端落在离竹子底端 3尺处，那么折断处离地面的高度为 尺.（1丈=10尺）三、解答题21 .我们从生活实际发现，当一个直角三角形两直角边长确定时，斜边长也就确定了.古代数学就已经发现，在直角三角形中，若两直角边长为a, b,斜边长为c,则已?十占二.这就是著名的“勾股定理”（1）如图1, 4个全等的直角三角形（其两直角边长为a, b,斜边长为c）与1个小正方形（边长为b）,不重叠无缝隙拼接成的正方形，请用这个图验证“勾

7、股定理”；（2）若直角三角形中两直角边的和b = 4 ,斜边c长为3,求直角三角形的面积；（3）如图2,若我2也中，2C=90° , JC=3 , HC = 4 ,点M是MB边上的动点，求线段Clf最短时的长度.22 .如图是用硬纸板做成的四个全等的直角三角形，两直角边的长分别为a和b,斜边长为c.请你开动脑筋，用它们拼出正方形图案，要求拼图时直角三角形纸片不能互相重叠.23 .济南的泉城广场视野开阔，阻挡物少，成为不少市民放风筝的最佳场所.历下区某校七年级（1）班的小明和小亮同学学习了 “勾股定理”之后，为了测得图中风筝的高度CE ,他们进行了如下操作：二AX JEf 77，测得SD的长为15米（注：8D±CE）；根据手中剩余线的长度计算出风筝线 BC的长为25米；牵线放风筝的小明身高 1.7米.（1）求风筝的高度C£ .过点小乍DH 阮,垂足为升，求的长度，24 .古埃及人曾用下面的方法得到直角：如图他们用13个等距的结把一根绳子分成等长的 12段，一个工匠同时握住绳子的第1个结和第1