2025年人教版高二数学上册月考试卷含答案

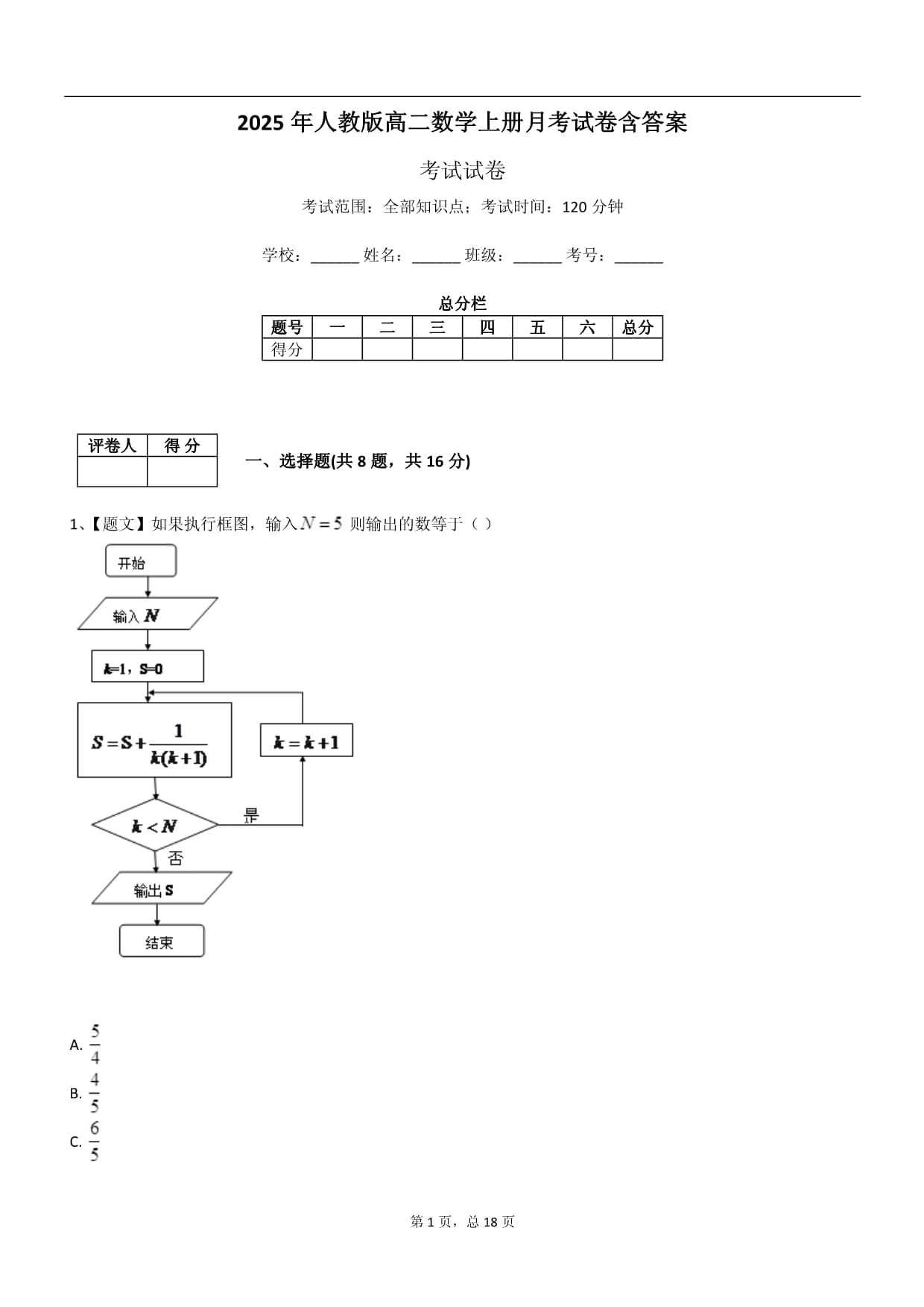
…………○…………内…………○…………装…………○…………内…………○…………装…………○…………订…………○…………线…………○…………※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※…………○…………外…………○…………装…………○…………订…………○…………线…………○…………第=page22页，总=sectionpages22页第=page11页，总=sectionpages11页2025年人教版高二数学上册月考试卷含答案考试试卷考试范围：全部知识点；考试时间：120分钟学校：______姓名：______班级：______考号：______总分栏题号一二三四五六总分得分评卷人得分一、选择题(共8题，共16分)1、【题文】如果执行框图，输入则输出的数等于（）

A.B.C.D.2、【题文】若三角形的两内角满足：则此三角形的形状为()A.锐角三角形B.钝角三角形C.直角三角形D.不能确定3、已知两直线a，b和两平面α，β，下列命题中正确的为（）A.若a⊥b且b∥α，则a⊥αB.若a⊥b且b⊥α，则a∥αC.若a⊥α且b∥α，则a⊥bD.若a⊥α且α⊥β，则a∥β4、已知a>0.b>0,,a,b等差中项是且,则最小值()A.3B.4C.5D.65、下列有关命题的说法正确的是（）A.命题“若x2=1，则x=1”的否命题为：“若x2=1，则x≠1”B.“x=-1”是“x2-5x-6=0”的必要不充分条件C.命题“若x=y，则sinx=siny”的逆否命题为真命题D.若命题p：“∃x0∈R使x02+x0+1＜0”，则￢p为假命题6、函数f（x）=（x≠-）满足f[f（x）]=x，则常数c等于（）A.3B.-3C.3或-3D.5或-37、正方体ABCD-A1B1C1D1的棱长为2，则D1到平面A1BD的距离为（）A.B.C.D.8、运行如图的程序；若输出的结果为9

则输入x

的值等于(

)

A.1

B.2

C.3

D.4

评卷人得分二、填空题(共6题，共12分)9、函数的定义域为若存在闭区间使得函数满足以下两个条件：(1)在[m，n]上是单调函数；(2)在[m，n]上的值域为[2m，2n]，则称区间[m，n]为的“倍值区间”．下列函数中存在“倍值区间”的有（填上所有正确的序号）①②③④10、【题文】某科研单位欲拿出一定的经费奖励科研人员，第1名得全部资金的一半多一万元，第2名得剩下的一半多一万元，以名次类推都得到剩下的一半多一万元，到第10名恰好资金分完，则此科研单位共拿出________万元资金进行奖励．11、【题文】在平面四边形ABCD中，点E，F分别是边AD，BC的中点，且ABCD．若则的值为____．12、【题文】已知在△ABC中，角A、B、C的对边分别为a，b，c。向量m=n=

若m⊥n，且则角C的大小是____13、【题文】已知向量m＝(a，b)，n＝(c，d)，p＝(x，y)，定义新运算m⊗n＝(ac＋bd，ad＋bc)，其中等式右边是通常的加法和乘法运算．如果对于任意向量m都有m⊗p＝m成立，则向量p＝________．14、记者要为4名志愿者和他们帮助的2位老人拍照，要求排成一排，2位老人相邻但不排在两端，则不同的排法有______．评卷人得分三、作图题(共5题，共10分)15、著名的“将军饮马”问题：有一位将军骑着马要从A地走到B地；但途中要到水边喂马喝一次水，则将军怎样走最近？

16、A是锐角MON内部任意一点，在∠MON的两边OM，ON上各取一点B，C，组成三角形，使三角形周长最小．（如图所示）17、已知，A，B在直线l的两侧，在l上求一点，使得PA+PB最小．（如图所示）18、著名的“将军饮马”问题：有一位将军骑着马要从A地走到B地；但途中要到水边喂马喝一次水，则将军怎样走最近？

19、A是锐角MON内部任意一点，在∠MON的两边OM，ON上各取一点B，C，组成三角形，使三角形周长最小．（如图所示）评卷人得分四、解答题(共2题，共12分)20、【题文】（本小题满分12分）

已知椭圆椭圆以的长轴为短轴,且与有相同的离心率.

(1)求椭圆的方程;

(2)设O为坐标原点,点A,B分别在椭圆和上,求直线的方程.21、用分析法证明：若a＞0，则+2≥a++．评卷人得分五、计算题(共1题，共4分)22、已知f（x）=∫1x（4t3﹣）dt，求f（1﹣i）•f（i）．评卷人得分六、综合题(共1题，共8分)23、如图，在直角坐标系中，点A，B，C的坐标分别为（-1，0），（3，0），（0，3），过AB，C三点的抛物的对称轴为直线l，D为对称轴l上一动点．

（1）求抛物线的解析式；

（2）求当AD+CD最小时点D的坐标；

（3）以点A为圆心；以AD为半径作⊙A．

①证明：当AD+CD最小时；直线BD与⊙A相切；

②写出直线BD与⊙A相切时，D点的另一个坐标：____．参考答案一、选择题(共8题，共16分)1、D【分析】【解析】

试题分析：第一次循环，第二次循环，第三次循环，第四次循环，第五次循环，此时不满足条件，输出选D.

考点：算法与框图.【解析】【答案】D2、B【分析】【解析】因为为三角形内角，所以从而有因为所以从而可得为钝角，所以此三角形为钝角三角形，故选B【解析】【答案】B3、C【分析】【解答】解：对于A，若a⊥b且b∥α；则a与α位置关系不确定；故A错误；

对于B，若a⊥b且b⊥α；则a与α位置关系不确定；可能平行；可能在平面内，也可能相交；故B错误；

对于C，若a⊥α且b∥α，根据线面垂直和线面平行的性质定理，可以得到a⊥b；故C正确；

对于D；若a⊥α且α⊥β，则a∥β或者a在平面β内，故D错误；

故选：C．

【分析】利用空间线面平行、线面垂直以及面面垂直的性质定理和判定定理对选项分别分析选择．4、C【分析】【分析】因为且等差中项是有a+b=1,那么则结合均值不等式的性质可知，取得等号，故选C.

【点评】解决该试题的关键是能整体利用合理的组合，结合均值不等式的思想，一正二定三相等的思想来求解最值。5、C【分析】解：命题“若x2=1，则x=1”的否命题为：“若x2≠1；则x≠1”，故A错误；

当“x=-1”时，“x2-5x-6=0”成立，当“x2-5x-6=0”时，“x=-1或x=6”，即“x=-1”不一定成立，故“x=-1”是“x2-5x-6=0”的充分不必要条件；故B错误；

命题“若x=y；则sinx=siny”为真命题，故命题“若x=y，则sinx=siny”的逆否命题为真命题，故C正确；

若命题p：“∃x0∈R使x02+x0+1＜0”为假命题；故￢p为真命题，故D错误；

故选：C

写出原命题的否命题；可判断A；根据充要条件的定义可判断B；根据原命题与逆否命题真假性相同可判断C；根据命题的否定与原命题真假性相反可判断D．

本题以命题的真假判断为载体，考查了四种命题，充要条件，复合命题等知识点，难度不大，属于基础题．【解析】【答案】C6、B【分析】解：∵函数满足f[f（x）]=x，∴x===

化为（2c+6）x2+（9-c2）x=0对于恒成立；

∴2c+6=9-c2=0；

解得c=-3．

故选B．

利用已知函数满足f[f（x）]=x，可得x===

化为（2c+6）x2+（9-c2）x=0对于恒成立；即可得出．

正确理解函数的定义和恒等式的意义是解题的关键．【解析】【答案】B7、D【分析】解：以D为原点，以DA为x轴，DC为y轴，DD1为z轴；建立空间直角坐标系；

∵正方体ABCD-A1B1C1D1的棱长为2；

∴D（0，0，0），A1（2，0，2），B（2，2，0），D1（0；0，2）；

∴

设面DBA1的法向量

∵

∴∴

∴D1到平面A1BD的距离d===．

故选D．

以D为原点，以DA为x轴，DC为y轴，DD1为z轴，建立空间直角坐标系，正方体ABCD-A1B1C1D1的棱长为2，知设面DBA1的法向量由知由向量法能求出D1到平面A1BD的距离．

本题考查点线面间的距离计算，是基础题，解题时要认真审题，仔细解答，注意向量法的合理运用．【解析】【答案】D8、B【分析】解：由程序可知；是顺序结构，输出的结果为9

所以由x3+5=9+4=13

解得：x=2

．

故选：B

．

通过程序；可知是顺序结构，根据输出结果，求出输入数值即可得到选项．

本题考查程序语句的应用，能够看出程序的结构类型，是解题的关键，属于基础题．【解析】B

二、填空题(共6题，共12分)9、略

【分析】试题分析：根据所给的定义，令f(x)=2x,解这个关于x的方程，只要存在两个不等的实根就行.①在［0,2］单调递增，值域为［0,4］，满足定义：②在R上单调递增，不存在这样的区间；③的区间是［0,1］,；④=2x,换元，转化为一元二次方程，利用△>0，便知有两个不等的实解.考点：定义题.【解析】【答案】①③④10、略

【分析】【解析】设第10名到第1名得到的奖金数分别是a1，a2，，a10，则an＝Sn＋1，则a1＝2，an－an－1＝＝(Sn－Sn－1)＝an，即an＝2an－1，因此每人得的奖金额组成以2为首项，以2为公比的等比数列，所以S10＝＝2046.【解析】【答案】204611、略

【分析】【解析】

试题分析：根据题意，由于平面四边形ABCD中，点E，F分别是边AD，BC的中点，且ABCD．若展开式可知=13；故可知答案为13.

考点：向量的数量积。

点评：主要是考查了向量的数量积的运算，属于中档题。【解析】【答案】12、略

【分析】【解析】解:由。

故角C的大小为【解析】【答案】13、略

【分析】【解析】∵m⊗p＝m，即(a，b)⊗(x，y)＝(ax＋by，ay＋bx)＝(a，b)，∴即．

由于对任意向量m＝(a，b)，都有(a，b)⊗(x，y)＝(a，b)成立，∴解得∴p＝(1,0)．【解析】【答案】(1,0)14、略

【分析】解：由题意知本题是一个分步问题；采用插空法；

先将4名志愿者排成一列；

再将2位老人看成一个整体插到4名志愿者形成的三个空中（除去两端的）；

然后将2位老人排列，则不同的排法有A44C31A22=144种；

故答案为144．

本题是一个分步问题；采用插空法，首先将4名志愿者排成一列，再将2位老人看成一个整体插到4名志愿者形成的三个空中，然后2位老人内部还有一个排列，根据分步计数原理得到结果．

本题考查分步计数原理；是一个基础题，题目中要求两个元素相邻的问题，一般把这两个元素看成一个元素进行排列，注意这两个元素内部还有一个排列；

属于中档题．【解析】144三、作图题(共5题，共10分)15、略

【分析】【分析】根据轴对称的性质作出B点与河面的对称点B′，连接AB′，AB′与河面的交点C即为所求．【解析】【解答】解：作B点与河面的对称点B′；连接AB′，可得到马喝水的地方C；

如图所示；

由对称的性质可知AB′=AC+BC；

根据两点之间线段最短的性质可知；C点即为所求．

16、略

【分析】【分析】作出A关于OM的对称点A'，关于ON的A对称点A''，连接A'A''，根据两点之间线段最短即可判断出使三角形周长最小的A、B的值．【解析】【解答】解：作A关于OM的对称点A'；关于ON的A对称点A''，与OM；ON相交于B、C，连接ABC即为所求三角形．

证明：∵A与A'关于OM对称；A与A″关于ON对称；

∴AB=A'B；AC=A''C；

于是AB+BC+CA=A'B+BC+A''C=A'A''；

根据两点之间线段最短，A'A''为△ABC的最小值．17、略

【分析】【分析】显然根据两点之间，线段最短，连接两点与直线的交点即为所求作的点．【解析】【解答】解：连接两点与直线的交点即为所求作的点P；

这样PA+PB最小；

理由是两点之间，线段最短．18、略

【分析】【分析】根据轴对称的性质作出B点与河面的对称点B′，连接AB′，AB′与河面的交点C即为所求．【解析】【解答】解：作B点与河面的对称点B′；连接AB′，可得到马喝水的地方C；

如图所示；

由对称的性质可知AB′=AC+BC；

根据两点之间线段最短的性质可知；C点即为所求．

19、略

【分析】【分析】作出A关于OM的对称点A'，关于ON的A对称点A''，连接A'A''，根据两点之间线段最短即可判断出使三角形周长最小的A、B的值．【解析】【解答】解：作A关于OM的对称点A'；关于ON的A对称点A''，与OM；ON相交于B、C，连接ABC即为所求三角形．

证明：∵A与A'关于OM对称；A与A″关于ON对称；

∴AB=A'B；AC=A''C；

于是AB+BC+CA=A'B+BC+A''C=A'A''；

根据两点之间线段最短，A'A''为△ABC的最小值．四、解答题(共2题，共12分)20、略

【分析】【解析】

试题分析：.(1)由已知可设椭圆的方程为

其离心率为故则

故椭圆的方程为

(2)解法一两点的坐标分别记为

由及(1)知,三点共线且点不在轴上,

因此可以设直线的方程为

将代入中,得所以

将代入中,则所以

由得即

解得故直线的方程为或

解法二两点的坐标分别记为

由及(1)知,三点共线且点不在轴上,

因此可以设直线的方程为

将代入中,得所以

由得

将代入中,得即

解得故直线的方程为或

考点：椭圆方程及性质。

点评：再求椭圆方程时要注意焦点的位置，第二问中向量关系转化为坐标关系,A,B两点坐标可将向量与两椭圆方程联系起来【解析】【答案】(1)(2)或21、略

【分析】

分析使不等式+2≥a++成立的充分条件；一直分析到使不等式成立的充分条件显然具备，从而不等式得证．

本题考查用分析法证明不等式，关键是寻找使不等式成立的充分条件．【解析】证明：要证+2≥a++

∵a＞0，∴两边均大于零，因此只需证（+2）2≥（a++）2（2分）

只需证≥（a+）；（4分）

只需证≥（+2）；（6分）

即证≥2；它显然成立．

∴原不等式成立．（8分）五、计算题(共1题，共4分)22、解：f（x）=（t4+）|1x=x4+﹣2f（1﹣i）=（1﹣i）4+﹣2=+

f（i）=i4+﹣2=﹣1﹣i

f（1﹣i）f（i）=6+5i【分析】【分析】先根据定积分求出函数f（x）的解析式，然后分别求出f（1﹣i）与f（i）即可求出所求．六、综合题(共1题，共8分)23、略

【分析】【分析】（1）由待定系数法可求得抛物线的解析式．

（2）连接BC；交直线l于点D，根据抛物线对称轴的性质，点B与点A关于直线l对称，∴AD=BD．

∴AD+CD=BD+CD；由“两点之间，线段最短”的原理可知：D在直线BC上AD+CD最短，所以D是直线l与直线BC的交点；

设出直线BC的解析式为y=kx+b；可用待定系数法求得BC直线的解析式，故可求得BC与直线l的交点D的坐标．

（3）由（2）可知，当AD+CD最短时，D在直线BC上，由于已