四川省仁寿2025届高三上学期一模诊断数学试卷（解析版）

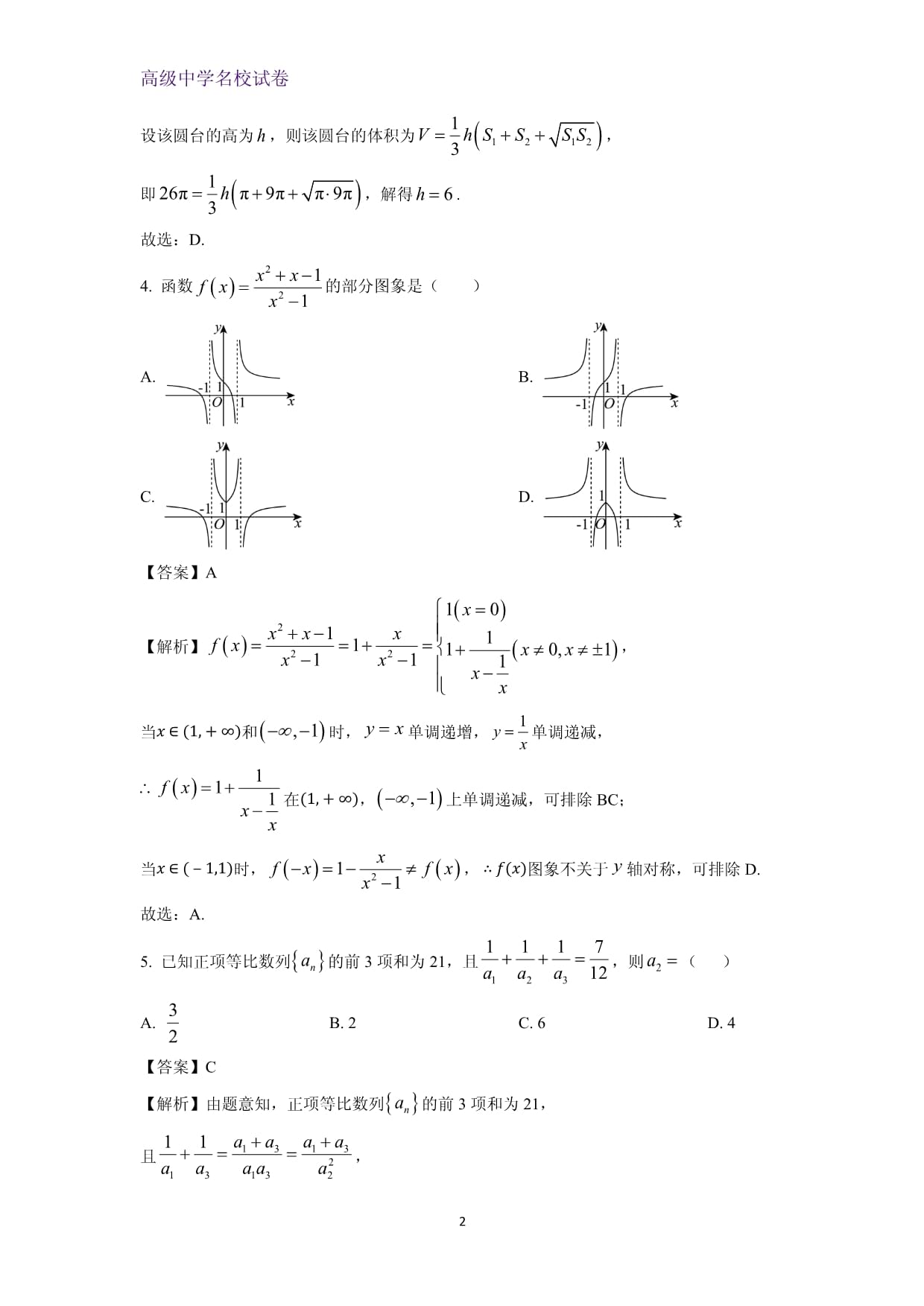
高级中学名校试卷PAGEPAGE1四川省仁寿2025届高三上学期一模诊断数学试卷一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.设集合，，则（）A. B.C D.【答案】A【解析】因为，，所以.故选：A.2.在平行四边形ABCD中，（）A. B.C. D.【答案】B【解析】在平行四边形ABCD中，，而，，，.故选：B.3.若某圆台的上、下底面的半径分别为1，3，且该圆台的体积为，则该圆台的高为（）A.3 B.4 C.5 D.6【答案】D【解析】由题可知，该圆台上底面圆的面积为，下底面圆的面积为，设该圆台的高为，则该圆台的体积为，即，解得.故选：D.4.函数的部分图象是（）A. B.C. D.【答案】A【解析】，当x∈1,+∞和时，单调递增，单调递减，在1,+∞，上单调递减，可排除BC；当x∈-1,1时，，∴fx图象不关于轴对称，可排除D.故选：A.5.已知正项等比数列的前3项和为21，且，则（）A. B.2 C.6 D.4【答案】C【解析】由题意知，正项等比数列的前3项和为21，且，则，解得.故选：C.6.曲线在点处的切线与坐标轴围成的三角形的面积为（）A. B. C. D.【答案】B【解析】由，得，则，所以曲线在点处的切线方程为，令，得；令，得，所以切线与坐标轴围成的三角形面积为.故选：B.7.已知，则的最大值为（）A. B. C. D.【答案】A【解析】因为，所以，所以，当且仅当，即时，等号成立，所以的最大值为.故选：A.8.若，，，则（）A. B.C. D.【答案】B【解析】，，，则，，下面比较与的大小，即比较与的大小，即比较与大小，即比较与的大小，而，则，所以.故选：B.二、选择题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.9.若复数，是方程的两个根，则（）A.为纯虚数 B.C. D.【答案】ABD【解析】方程，，方程的根为，即方程的根为，，不妨设，，则为纯虚数，故A正确；，故B正确；，故C错误；，则，故D正确.故选：ABD.10.已知函数的部分图象如图所示，其中，，则（）A. B.C.在上单调递增 D.在上恰有10个零点【答案】ABD【解析】由图可知，，，即，又，则，故A正确；此时，又，且，则，故B正确；此时，当时，，因为函数在上不单调，所以在上不单调，故C错误；当时，，因为函数在上有10个零点，所以在上恰有10个零点，故D正确.故选：ABD.11.在体积为的正四棱锥中，异面直线PC与AB所成角的余弦值为，则（）A.B.二面角的余弦值为C.正四棱锥的外接球的表面积为D.直线BC与平面PCD所成角的正切值为2【答案】BCD【解析】取的中点，设为正方形的中心，连接，，则.因为，所以异面直线与所成的角即，则.设，则，，，则，所以正四棱锥的体积为，解得，所以，故A错误.在正方形中，由于，为的中点，所以，则为二面角的平面角，所以，故B正确.设正四棱锥的外接球的球心为，且，又，由，得，解得，所以正四棱锥的外接球的表面积为，故C正确.因为，所以直线与平面所成的角即直线与平面所成的角.过点作，垂足为，因为平面，且平面，所以，又，且平面，所以平面，又平面，所以，又，且平面，所以平面，则为直线与平面所成的角，则，故D正确.故选：BCD.三、填空题：本题共3小题，每小题5分，共15分.12.若钝角满足，则______.【答案】5【解析】由题意，，则，所以，由，解得.13.已知是奇函数，当时，，则______.【答案】【解析】由是奇函数，得函数关于对称，又当时，，则.14.在如图所示的方格表中选5个方格，则这5个方格的数中恰有2个11的概率为______，若要求每行和每列都恰有1个方格被选中，则被选方格的5个数之和的最大值为______.10213041501120304049101929405111203139501123324352【答案】【解析】由题知表中共有25个数，其中包含3个11，所以任选5个方格，其中恰有2个11的概率为.根据题表知每列数字最大值都在最后一行出现，根据题表可得出每列数字与此列中最大数的差的绝对值，如下表：1222203233143310314200000按要求每行和每列都恰有1个方格被选中，若被选方格的5个数之和最大，则差的绝对值之和最小，所以要使得5个数之和最大，则这5个数可以为11，23，31，41，51，此时和为，即和的最大值为.四、解答题：本题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤.15.已知的内角A，B，C的对边分别为，，，且.（1）求的大小；（2）若的面积为，求外接圆的直径.解：（1）因为，由正弦定理得，，不妨设，，则由余弦定理得，，又，则.（2）设外接圆的半径为，由题意，，即，由（1）知，设，，则，解得，则，所以，则外接圆的直径为.16.如图，四边形ABCD是正方形，AE，DF，BG都垂直于平面ABCD，且，，，M，N分别是EG，BC的中点.（1）证明：平面ABCD.（2）若，求点N到平面AMF的距离.（1）证明：因为，，都垂直于平面，则.取的中点，连接，，则，且，所以且，所以四边形为平行四边形，可得，且平面，平面，所以平面.（2）解：连接.以为坐标原点，，，所在直线分别为轴，轴，轴，建立如图所示的空间直角坐标系，则A2,0,0，，，，可得，，.设平面的法向量为n=x,y,z，则，取，得，，可得.故点到平面的距离.17.在递增的等差数列中，，.（1）求的通项公式；（2）求数列的前项和.解：（1）设的公差为，因为数列是等差数列，所以，由解得，所以，所以.（2）由（1）可得，则①，②，①-②得则.18.某工厂打算购买2台设备，该设备有一种易损零件，在购买设备时可以额外购买这种易损零件作为备件，价格为每个200元.在设备使用期间，零件损坏，备件不足再临时购买该零件，价格为每个320元.在使用期间，每台设备需要更换的零件个数T的分布列为45670.30.20.40.1表示2台设备使用期间需更换的零件个数，代表购买2台设备的同时购买易损零件的个数.（1）求的分布列；（2）以购买易损零件所需费用的期望为决策依据，试问在和中，应选择哪一个?解：（1）由题意，的可能取值为8，9，10，11，12，13，14，则，，，，，，，则的分布列为：8910111213140.090.120.280.220.20.080.01（2）记为当时购买零件所需费用，的可能取值为2000，2320，2640，2960，3280，则，，，，，则.记为当时购买零件所需费用，的可能取值为2200，2520，2840，3160，则，，，，，显然，所以应选择.19.若存在有限个，使得，且不是偶函数，则称为“缺陷偶函数”，称为的偶点.（1）证明：为“缺陷偶函数”，且偶点唯一.（2）对任意x，，函数，都满足.①若是“缺陷偶函数”，证明：函数有2个极值点.②若，证明：当时，.参考数据：，.解：（1）由可得，由可得，解得，所以为“缺陷偶函数”，且偶点唯一，且为0，（2）由可得对