数学自我小测：回归分析

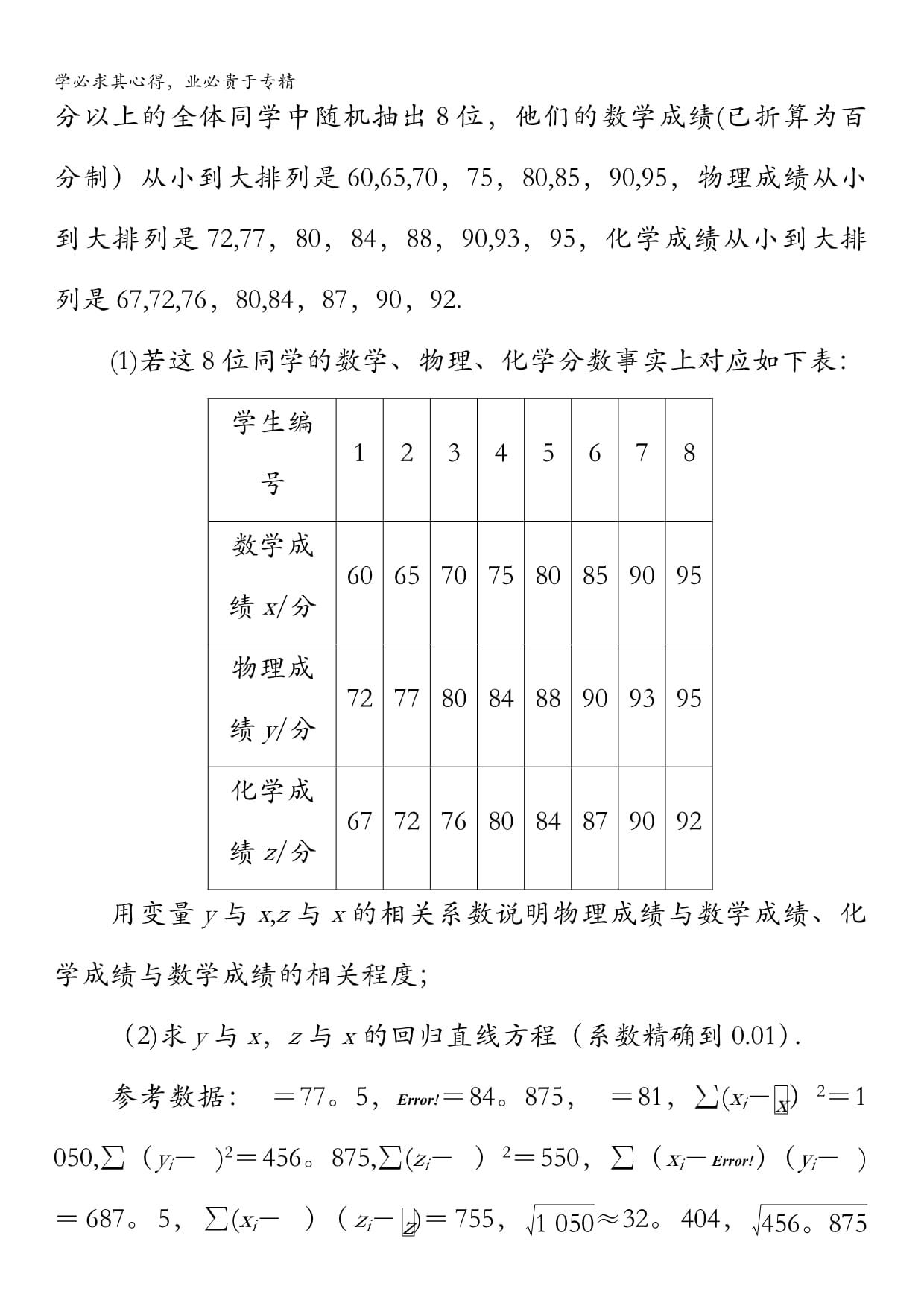
学必求其心得，业必贵于专精学必求其心得，业必贵于专精学必求其心得，业必贵于专精自我小测1．设两个变量x和y之间具有线性相关关系，它们的相关系数是r，y关于x的回归直线的斜率是eq\o（b,\s\up6（^)）,纵截距是eq\o（a,\s\up6（^）），那么必有（）A.eq\o(b,\s\up6（^）)与r的符号相同 B。eq\o(a，\s\up6(^)）与r的符号相同C.eq\o（b,\s\up6(^))与r的符号相反 D.eq\o(a,\s\up6（^))与r的符号相反2．设有一个回归直线方程为eq\o(y,\s\up6(^）)＝3－5x,则当变量x增加1个单位时(）A．y平均增加3个单位 B．y平均减少5个单位C．y平均增加5个单位 D．y平均减少3个单位3．变量X与Y相对应的一组数据为（10,1），(11.3,2)，（11.8，3),(12.5,4），(13，5);变量U与V相对应的一组数据为(10,5），(11。3,4)，（11。8,3)，(12。5，2)，(13,1)．r1表示变量Y与X之间的相关系数，r2表示变量V与U之间的相关系数，则（）A．r2＜r1＜0B．0＜r2＜r1C．r2＜0＜r1D．r2＝r14．在一组样本数据(x1，y1)，（x2,y2），…，(xn,yn)（n≥2，x1，x2，…，xn不全相等）的散点图中，若所有样本点（xi，yi)（i＝1，2，…，n）都在直线y＝eq\f（1,2)x＋1上，则这组样本数据的样本相关系数为（）A．－1B．0C。eq\f（1，2)D．15．为了解儿子身高与其父亲身高的关系，随机抽取5对父子的身高数据如下：父亲身高x/cm174176176176178儿子身高y/cm175175176177177则y对x的回归直线方程为（)A.eq\o(y,\s\up6(^))＝x－1B。eq\o（y,\s\up6(^))＝x＋1C.eq\o（y,\s\up6（^)）＝88＋eq\f(1,2）xD。eq\o（y，\s\up6(^))＝1766．设某大学的女生体重y（单位：kg）与身高x(单位:cm)具有线性相关关系，根据一组样本数据(xi，yi)(i＝1，2，…，n)，用最小二乘法建立的回归直线方程为eq\o(y，\s\up6(^）)＝0.85x－85。71，则下列结论中不正确的是()A．y与x具有正的线性相关关系B．回归直线过样本点的中心(eq\x\to(x)，eq\x\to(y))C．若该大学某女生身高增加1cm，则其体重约增加0.85kgD．若该大学某女生身高为170cm，则可断定其体重必为58.79kg7．对四组变量y和x进行线性相关性检验，已知n是观测值组数，r是相关系数．已知①n＝7,r＝0.9545；②n＝15,r＝0.3812；③n＝17，r＝0。4985;④n＝3，r＝0。9870，则变量y与x具有线性相关关系的是__________．8．图书馆工作人员想知道每天到图书馆的人数x（百人)与借出的图书本数y（百本)之间的关系,已知上个月图书馆共开放25天，且得到资料：∑xi＝200，∑yi＝300，∑xeq\o\al(2，）i＝1660，∑yeq\o\al（2，）i＝3696，∑xiyi＝2436，则y对x的回归直线方程为__________．9．已知x,y的取值如下表所示:x0134y2。24.34.86.7从散点图分析，y与x线性相关，且eq\o（y,\s\up6(^))＝0.95x＋eq\o（a，\s\up6（^)）,则eq\o（a,\s\up6(^）)＝__________。10．已知10只狗的血球体积x(单位：mm3）及红血球数y(单位：百万）的测量值如下：x45424648423558403950y6.536.309.257.506。995.909。496.206。557。72（1)画出散点图;（2)求出y对x的回归直线方程；(3)若血球体积为49mm3,预测红血球数大约是多少?11．下表是美国旧轿车价格的调查资料，今以x表示轿车的使用年数,y表示相应的平均价格,求y关于x的非线性回归方程．使用年数x12345678910平均价格(美元)y265119431494108776553848429022620412．为了对2014年佛山市某中学的中考成绩进行分析，在60分以上的全体同学中随机抽出8位，他们的数学成绩(已折算为百分制）从小到大排列是60,65,70，75，80,85，90,95，物理成绩从小到大排列是72,77，80，84，88，90,93，95，化学成绩从小到大排列是67,72,76，80,84，87，90，92.(1)若这8位同学的数学、物理、化学分数事实上对应如下表：学生编号12345678数学成绩x/分6065707580859095物理成绩y/分7277808488909395化学成绩z/分6772768084879092用变量y与x,z与x的相关系数说明物理成绩与数学成绩、化学成绩与数学成绩的相关程度；（2)求y与x，z与x的回归直线方程（系数精确到0.01）．参考数据：eq\x\to(x）＝77。5，eq\x\to（y)＝84。875，eq\x\to（z）＝81，∑(xi－eq\x\to(x)）2＝1050,∑（yi－eq\x\to（y）)2＝456。875,∑(zi－eq\x\to(z））2＝550，∑（xi－eq\x\to（x)）（yi－eq\x\to(y）)＝687。5，∑(xi－eq\x\to(x））（zi－eq\x\to(z))＝755，eq\r(1050)≈32。404，eq\r(456。875)≈21.375,eq\r（550)≈23.452。

参考答案1.解析：由回归直线方程的斜率eq\o(b，\s\up6(^)）与相关系数r的计算公式可以得出结论．答案：A2.解析：因为－5是斜率的估计值,说明x每增加1个单位时，y平均减少5个单位．答案：B3.解析：∵r＝eq\f(∑(xi－\x\to(x）)(yi－\x\to（y)）,\r(∑（xi－\x\to(x）)2）\r(∑（yi－\x\to（y））2）)，∴通过计算得第一组变量正相关，第二组变量负相关．故选C。答案：C4。解析：样本相关系数越接近1，相关性越强，若所有的样本点都在直线y＝eq\f（1,2）x＋1上，则样本相关系数应为1。答案：D5。解析：法一：由回归直线方程过样本中心（176，176），排除A，B答案，结合选项可得C为正确答案．法二：将表中的五组数值分别代入选项验证，可知eq\o(y，\s\up6（^))＝88＋eq\f（1，2）x最适合．答案:C6。解析：∵0.85＞0,∴y与x正相关，∴A正确；∵回归直线方程经过样本点的中心(eq\x\to(x）,eq\x\to（y)），∴B正确；∵Δy＝0。85×（x＋1）－85.71－（0.85x－85.71）＝0。85，∴C正确．故选D.答案：D7.解析：①r＞r0。05＝0.754，②r＜r0。05＝0.514,③r＞r0。05＝0.482,④r＜r0.05＝0.997,从而①③正确．答案：①③8。解析:将已知量代入回归直线方程可得eq\o（a,\s\up6(^))＝7。2，eq\o（b，\s\up6(^))＝0.6。答案：eq\o（y，\s\up6（^）)＝7。2＋0.6x9。解析：eq\x\to（x)＝eq\f（1,4)（0＋1＋3＋4)＝2，eq\x\to（y)＝eq\f(1，4）(2.2＋4.3＋4。8＋6.7）＝4.5.回归直线方程过（2,4。5），则4.5＝0.95×2＋eq\o(a,\s\up6(^))，eq\o（a，\s\up6（^)）＝2.6。答案：2。610.解：（1）散点图如图所示．(2)设回归直线方程为eq\o(y，\s\up6(^))＝eq\o（b,\s\up6（^））x＋eq\o（a，\s\up6（^)），由表中数据代入公式，得eq\o（b,\s\up6(^)）＝eq\f(∑xiyi－10\x\to(x)\x\to（y),∑x2i－10\x\to（x)2）＝0。16，eq\o(a,\s\up6(^))＝eq\x\to（y）－eq\o(b，\s\up6（^））eq\x\to（x）＝0。12。所以所求回归直线方程为eq\o(y，\s\up6(^))＝0。16x＋0.12。(3）x＝49代入回归直线方程,得eq\o(y,\s\up6（^)）＝0.16×49＋0.12＝7.96（百万)，计算结果表明，当血球体积为49mm3时，红血球数大约为7.96百万．11。解：作散点图如图所示．由散点图看出y与x呈指数关系，于是令z＝lny。变换后得数据:x12345z7.8837。5727。3096.9916。640x678910z6.2886。1825。6705.4215.318画出散点图如图所示:由图可知，各点基本上处于一直线，由表中数据可得回归直线方程:eq\o（z,\s\up6(^)）＝8。166－0.298x。因此旧车的平均价格对使用年数的非线性回归方程为eq\o(y，\s\up6(^）)＝e8。166－0.298x.12。分析：利用样本相关系数公式求出r,再利用r的值分析两变量之间相关程度的大小．解：(1）变量y与x，z与x的相关系数分别是r＝eq\f(∑（xi－\x\to（x)）(yi－\x\to（y）），\r（∑（xi－\x\to(x))2∑(yi－\x\to(y）)2））＝eq\f（687.5,\r(1050×456。875))＝0.993,r′＝eq\f（∑（xi－\x\to(x）)(zi－\x\to（z）)，\r（∑(xi－\x\to(x））2∑（zi－\x\to（z))2）)＝eq\f(755，\r(1050×550））＝0。994，可以看出物理成绩与数学成绩、化学成绩与数学成绩之间都是高度正相关的．(2)设y与x，z与x的回归直线方程分别是eq\o(y，\s\up6(^))＝eq\o（b,\s\up6（^））x＋eq\o(a，\s\up6（^）)，eq\o(z,\s\up6（^))＝eq\o(b,\s\up6（^))′x＋eq\o(a，\s\up6（^））′，根据所给的数据，可以计算出eq\o(b，\s\up6（^)）＝eq\f(∑(xi－\x\to（x)）(yi－\x\to（y）),∑（xi－\x\to(x)）2)＝eq\f（687。5,1050)＝0.65，eq\o（a,\s\up6（^））＝eq\x\to（y）－eq\o(b,\s\up6(^）)eq\x\to(x)＝34.