2024-2025学年新教材高中数学课时作业13第十一章立体几何11.1.4棱锥与棱台含解析新人教B版必修第四册

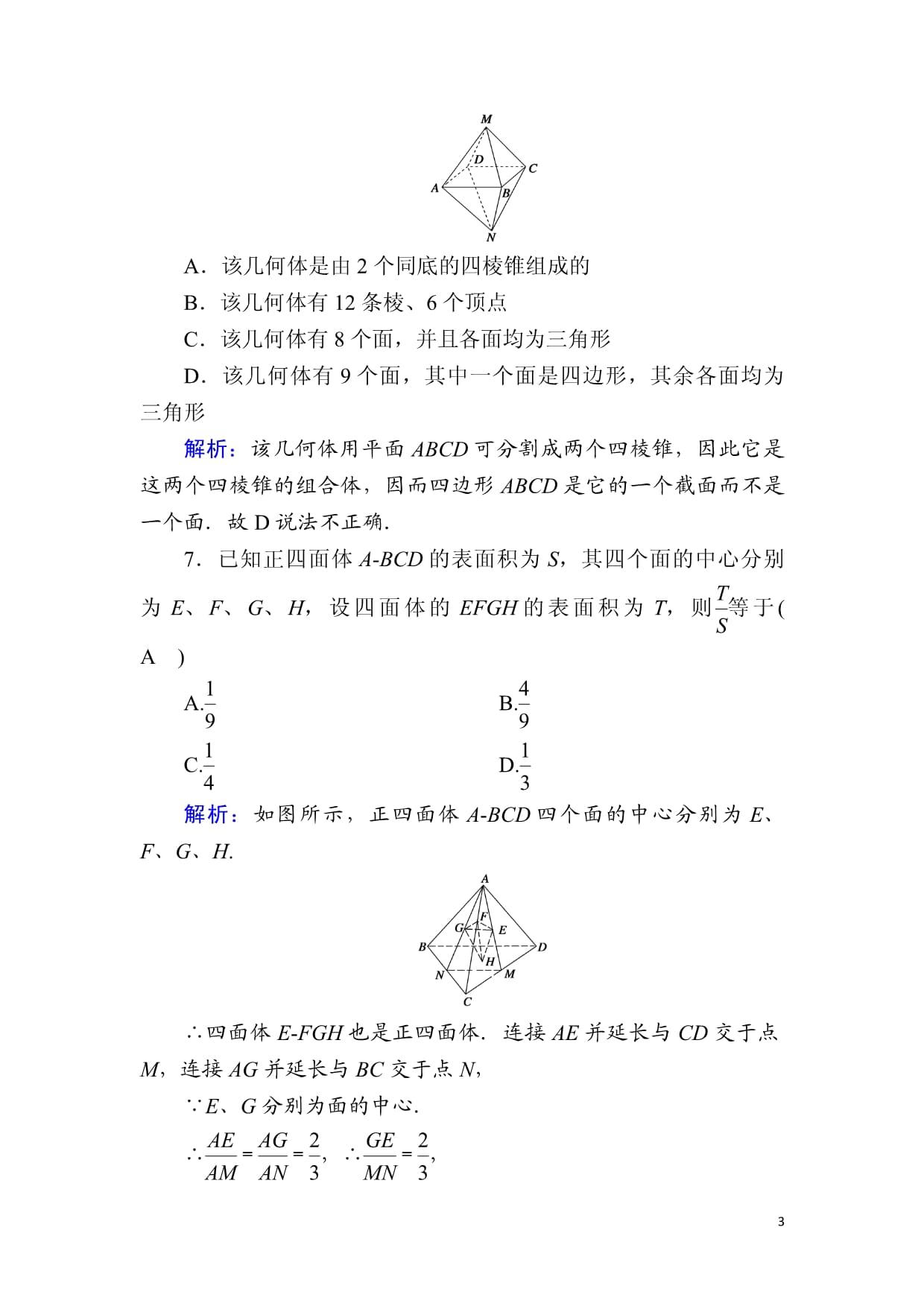
PAGEPAGE1课时作业13棱锥与棱台时间：45分钟eq\a\vs4\al(一、选择题每小题5分，共40分)1．(多选)关于多面体的结构特征，下列说法正确的是(ACD)A．棱柱的侧棱长都相等B．棱锥的侧棱长都相等C．三棱台的上、下底面是相像三角形D．有的棱台的侧棱长都相等解析：依据棱锥的结构特征知，棱锥的侧棱相交于一点但长度不肯定相等．2．以三棱台的顶点为三棱锥的顶点，这样可以把一个三棱台分成的三棱锥的个数是(C)A．1B．2C．3D．4解析：如图，分割为A1­ABC，B­A1B1C1，C1­A1BC,3个棱锥．3．下列三种叙述，正确的有(A)①用一个平面去截棱锥，棱锥底面和截面之间的部分是棱台；②两个面平行且相像，其余各面都是梯形的多面体是棱台；③有两个面相互平行，其余四个面都是等腰梯形的六面体是棱台．A．0个B．1个C．2个D．3个解析：①中的平面不肯定平行于底面，故①错；②③可用反例去检验，如图所示，侧棱延长线不能相交于一点，故②③错．故选A.4．正四棱台的上、下底面均为正方形，它们的边长分别为2cm和6cm，两底面之间的距离为2cm，则四棱台的侧棱长为(C)A．3cm B．2eq\r(2)cmC．2eq\r(3)cm D.eq\r(5)cm解析：如图，由题设可知O1B1＝eq\r(2)，OB＝3eq\r(2)，OO1＝2，故侧棱长BB1＝eq\r(22＋3\r(2)－\r(2)2)＝2eq\r(3)(cm)．5．侧棱长为2a的正三棱锥，若底面周长为9a，则棱锥的高是(A)A．a B．2aC.eq\f(\r(3),2)a D.eq\f(\r(2),2)a解析：如图，由题意知AB＝BC＝AC＝3a，∴OC＝eq\f(2,3)·eq\f(\r(3),2)·3a＝eq\r(3)a.∴SO＝eq\r(SC2－OC2)＝eq\r(4a2－3a2)＝eq\r(a2)＝a.6.如图所示的几何体，关于其结构特征，下列说法错误的是(D)A．该几何体是由2个同底的四棱锥组成的B．该几何体有12条棱、6个顶点C．该几何体有8个面，并且各面均为三角形D．该几何体有9个面，其中一个面是四边形，其余各面均为三角形解析：该几何体用平面ABCD可分割成两个四棱锥，因此它是这两个四棱锥的组合体，因而四边形ABCD是它的一个截面而不是一个面．故D说法不正确．7．已知正四面体A­BCD的表面积为S，其四个面的中心分别为E、F、G、H，设四面体的EFGH的表面积为T，则eq\f(T,S)等于(A)A.eq\f(1,9) B.eq\f(4,9)C.eq\f(1,4) D.eq\f(1,3)解析：如图所示，正四面体A­BCD四个面的中心分别为E、F、G、H.∴四面体E­FGH也是正四面体．连接AE并延长与CD交于点M，连接AG并延长与BC交于点N，∵E、G分别为面的中心．∴eq\f(AE,AM)＝eq\f(AG,AN)＝eq\f(2,3)，∴eq\f(GE,MN)＝eq\f(2,3)，又∵MN＝eq\f(1,2)BD，∴eq\f(GE,BD)＝eq\f(1,3)，∵面积比是相像比的平方，∴eq\f(T,S)＝eq\f(1,9).8．正四棱锥的侧棱长是底面边长的k倍，则k的取值范围是(D)A．(0，＋∞) B.eq\b\lc\(\rc\)(\a\vs4\al\co1(\f(1,2)，＋∞))C．(eq\r(2)，＋∞) D.eq\b\lc\(\rc\)(\a\vs4\al\co1(\f(\r(2),2)，＋∞))解析：由正四棱锥的定义(如图)知正四棱锥S­ABCD中，S在底面ABCD内的射影O为正方形的中心，而SA>OA＝eq\f(\r(2),2)AB，∴eq\f(SA,AB)>eq\f(\r(2),2)，即k>eq\f(\r(2),2).eq\a\vs4\al(二、填空题每小题6分，共18分)9．已知正四棱锥V­ABCD中，底面面积为16，一条侧棱的长为2eq\r(11)，则该棱锥的高为6.解析：取正方形ABCD的中心O，连接VO，AO，则VO就是正四棱锥V­ABCD的高．∵底面面积为16，∴AO＝2eq\r(2).∵一条侧棱长为2eq\r(11)，∴VO＝eq\r(VA2－AO2)＝eq\r(44－8)＝6.∴正四棱锥V­ABCD的高为6.10．如图，能推断这个几何体可能是三棱台的是③.(填序号)①A1B1＝2，AB＝3，B1C1＝3，BC＝4；②A1B1＝1，AB＝2，B1C1＝1.5，BC＝3，A1C1＝2，AC＝3；③A1B1＝1，AB＝2，B1C1＝1.5，BC＝3，A1C1＝2，AC＝4；④A1B1＝AB，B1C1＝BC，C1A1＝CA.解析：因为三棱台的上下底面相像，所以该几何体假如是三棱台，则△A1B1C1∽△ABC，所以eq\f(A1B1,AB)＝eq\f(B1C1,BC)＝eq\f(A1C1,AC).故选③.11．有一个正四面体的棱长为3，现用一张圆形的包装纸将其完全包住(不能裁剪纸，但可以折叠)，那么包装纸的最小半径为2eq\r(3).解析：由题意，将正四面体沿底面将侧面都绽开，如图所示．绽开图是由4个边长为3的小正三角形组成的一个边长为6的大正三角形，设底面正三角形的中心为O，不难得到当包装纸是大正三角形的外接圆时，所需包装纸的半径最小，此时由正弦定理可得包装纸的最小直径为：2R＝eq\f(6,sin\f(π,3))＝4eq\r(3)，所以包装纸的最小半径为2eq\r(3).三、解答题写出必要的计算步骤，只写最终结果不得分，12、13、15题各12分，14题6分，共42分12．试从正方体ABCD­A1B1C1D1的八个顶点中任取若干个点，连接后构成以下空间几何体，并且用适当的符号表示出来．(1)只有一个面是等边三角形的三棱锥；(2)四个面都是等边三角形的三棱锥；(3)三棱柱．解：(1)如图所示，三棱锥A1­AB1D1(答案不唯一)．(2)如图所示，三棱锥B1­ACD1(答案不唯一)．(3)如图所示，三棱柱A1B1D1­ABD(答案不唯一)．13．正四棱台的体对角线长是5cm，高是3cm，求它的相对侧棱所确定的截面面积．解：如图(1)所示，面ACC1A1是相对的两条侧棱AA1和CC1所确定的截面，它的对角线长即是正四棱台的体对角线长，∴A1C＝5cm，OO1＝3cm.其截面又可画成图(2)的形态，由点A1向AC作垂线交AC于H，则A1H＝OO1＝3cm.∴CH＝4cm，又∵AH＋A1C1＝CH，∴S四边形ACC1A1＝eq\f(1,2)(AC＋A1C1)·A1H＝eq\f(1,2)·2CH·A1H＝4×3＝12(cm2)．∴相对侧棱所确定的截面面积为12cm2.——素养提升——14．如图，已知正三棱锥P­ABC的侧棱长为eq\r(2)，底面边长为eq\r(2)，Q是侧棱PA的中点，一条折线从A点动身，绕侧面一周到Q点，则这条折线长度的最小值为eq\f(3\r(2),2).解析：如图，沿着棱PA把三棱锥绽开成平面图形，所求的折线长度的最小值就是线段AQ的长度，因为点Q是PA′的中点，所以在绽开图中，AQ＝eq\f(3\r(2),2).15.如图，正六棱锥的底面周长为24，H是BC的中点，O为底面六边形中心，∠SHO＝60°.求：(1)棱锥的高；(2)斜高；(3)侧棱长．解：∵正六棱锥的底面周长为24，∴正六棱锥的底面边长为4.在正六棱锥S­ABCDEF中，∵H是BC的中点，∴SH⊥B