6 应用一元二次方程 数学北师大版九年级上册

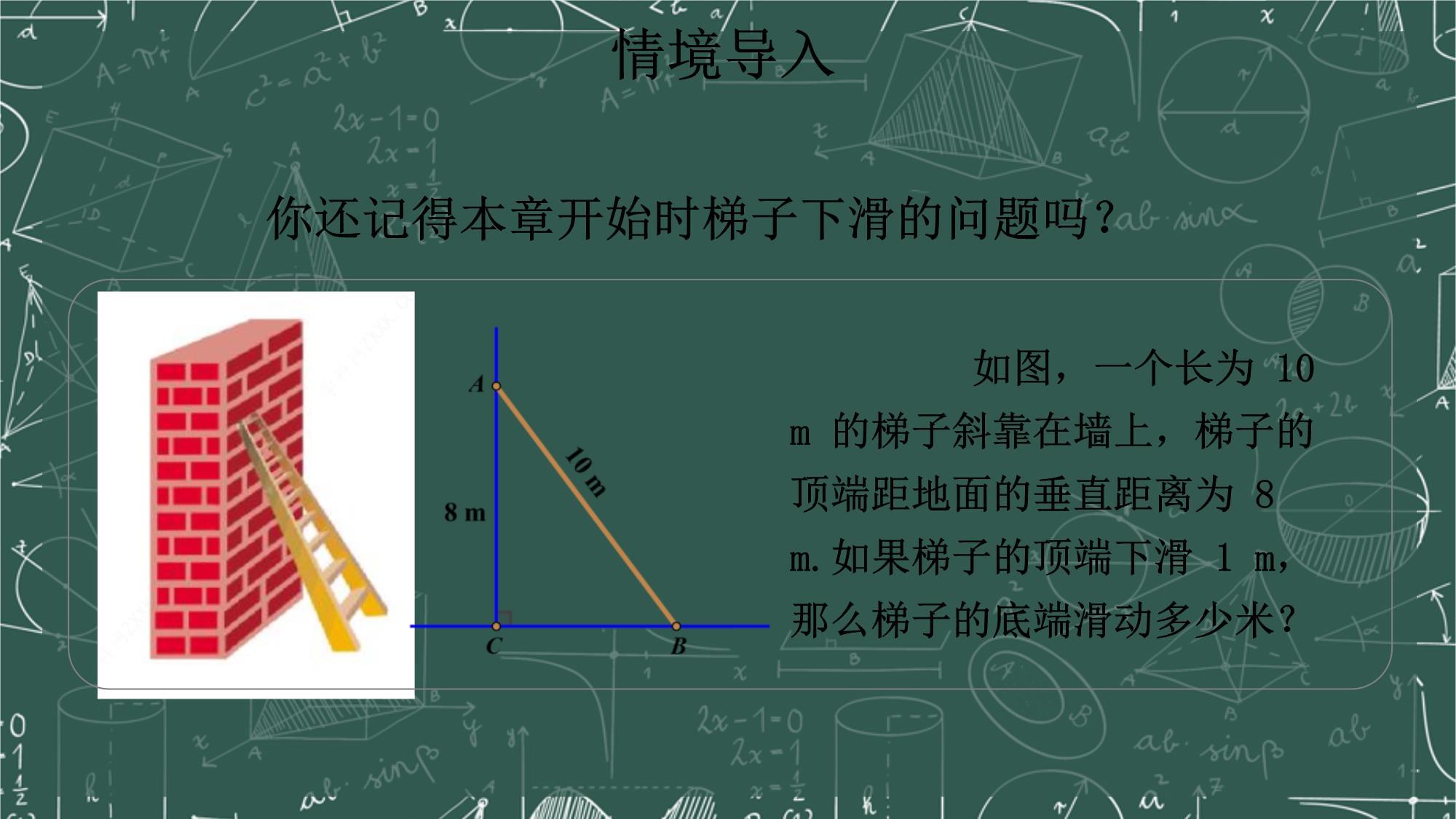
第二章一元二次方程6应用一元二次方程初中数学北师大版九年级上册第1课时利用一元二次方程解决几何问题情境导入你还记得本章开始时梯子下滑的问题吗？如图，一个长为10

m

的梯子斜靠在墙上，梯子的顶端距地面的垂直距离为8

m.如果梯子的顶端下滑1

m，那么梯子的底端滑动多少米？（1）在这个问题中，梯子顶端下滑1米时，梯子底端滑动的距离大于1米，那么梯子顶端下滑几米时，梯子底端滑动的距离和它相等呢？xx设梯子顶端下滑x米，底端滑动x米(8-x)2+(6+x)2=102x2-2x=0x1=0（舍），x2=2.（2）如果梯子长度是13m，梯子顶端与地面的垂直距离为12m，那么梯子顶端下滑的距离与梯子底端滑动的距离可能相等吗？如果相等，那么这个距离是多少？设梯子顶端下滑x米，底端滑动x米(12-x)2+(5+x)2=132x2-7x=0x1=0（舍），x2=7.几何画板探究新知例1如图：某海军基地位于A处，在其正南方向200海里处有一重要目标B，在B的正东方向200海里处有一重要目标C，小岛D位于AC的中点，岛上有一补给码头。小岛F位于BC中点。一艘军舰从A出发，经B到C匀速巡航，一艘补给船同时从D出发，沿南偏西方向匀速直线航行，欲将一批物品送达军舰。已知军舰的速度是补给船的2倍，军舰在由B到C的途中与补给船相遇，那么相遇时补给船航行了多少海里？（结果精确到0.1海里）几何画板（1）要求

DE

的长，需要如何设未知数？

（2）怎样建立含

DE未知数的等量关系？从已知条件中能找到吗？（3）利用勾股定理建立等量关系，如何构造直角三角形？（4）选定Rt△DEF后，三条边长都是已知的吗？DE，DF，EF分别是多少？解：连接DF.∵AD=CD，BF=CF，∴DF是△ABC

的中位线.∴DF∥AB，且DF=AB.∵AB⊥BC，DF=100nmile，BF=100nmile.设相遇时补给船航行了xnmile，那么DE=xnmile，AB+BE=2xnmile，EF=AB+BF-（AB+BE）=（300-2x）nmile.在Rt△DEF

中，根据勾股定理可得方程

x2=1002+(300-2x)2，整理，得3x2-1200x+100000=0.

解这个方程，得

所以，相遇时补给船大约航行了118.4nmile.随堂练习【选自教材P53随堂练习】《九章算术》“勾股”章有一题：“今有二人同所立，甲行率七，乙行率三，乙东行，甲南行十步而斜东北与乙会，问甲乙行各几何。”大意是说：已知甲、乙二人同时从同一地点出发，甲的速度为7，乙的速度为3。乙一直向东走，甲先向南走了10步，后又斜向北偏东方向走了一段后与乙相遇。那么相遇时，甲、乙各走了多远？解：设所行时间为t，则有(3t)2+102=(7t-10)2，解得t1=0（舍去），t2=.∴甲走了×7=（步），乙走了×3=（步）.达标检测【选自教材P53习题2.9】有这样一道阿拉伯古算题：有两笔钱，一多一少，其和等于20，积等于96，多的一笔钱被许诺赏给赛义德，那么赛义德得到多少钱？解:设较多的钱为x．由题意,可得x(20－x)＝96，解得x1＝12，x2＝8(舍去)．所以，赛义德得到的钱数为12.如图：在Rt△ACB中，∠C=90°，点P、Q

同时由A、B两点出发分别沿AC、BC方向向点C

匀速移动，它们的速度都是1m/s，几秒后△PCQ的面积为Rt△ACB面积的一半？解:设经过ts，△PCQ

面积为Rt△ACB

面积的一半．

(8－t)(6－t)＝×6×8×，解得t1＝2，t2＝12(舍去)．所以，经过2s，△PCQ

面积为Rt△ACB

面积的一半．【选自教材P53习题2.9】如图，一条水渠的断面为梯形，已知断面的面积为0.78m2，上口比渠底宽0.6，渠深比渠底少0.4m，求渠深.【选自教材P53习题2.9】解:设渠深为xm，则渠底为(x＋0.4)m．S＝·[(x＋0.4＋0.6＋x＋0.4)]·x

＝0.78，解得x1＝－1.3(舍去)，x2＝0.6．所以，渠深0.6m．解:设

ts后P

，Q

两点相距15cm．由题意有t2＋(21－t)2＝152，解得t1＝9，t2＝12．所以，运动9s或12s时,P,Q

两点相距15cm．如图，在Rt△ACB

中，∠C=90°，AC=30cm，BC=21cm.动点P从点C出发，沿CA方向运动；动点Q同时从点B出发，沿BC方向运动.如果动点P，Q的运动速度均为1cm/s，那么运动几秒时，它们相距15cm？.【选自教材P54习题2.9】第二章一元二次方程6应用一元二次方程初中数学北师大版九年级上册第2课时利用一元二次方程解决经济问题知识回顾请同学们回忆并回答与利润相关的知识利润=（）-

进价售价售价=标价×折扣9折要乘以90%或0.9或，那么x

折呢？探究新知例2新华商场销售某种冰箱，每台进货价为2500元。市场调研表明：当销售价为2900元时，平均每天能售出8台；而当销售价每降低50元时，平均每天就能多售出4台。商场要想使这种冰箱的销售利润平均每天达到5000元，每台冰箱的降价应为多少元？分析基本数量关系售价-进价=利润每台利润×每天的销售量=每天的总利润例2新华商场销售某种冰箱，每台进货价为2500元。市场调研表明：当销售价为2900元时，平均每天能售出8台；而当销售价每降低50元时，平均每天就能多售出4台。商场要想使这种冰箱的销售利润平均每天达到5000元，每台冰箱的降价应为多少元？进价售价销售量每台利润总利润降价前降价后250029008400400×82500未知未知未知5000设每台冰箱降价x

元售价每降低50元多售出4台售价每降低100元多售出4×台售价每降低x

元多售出4×台例2新华商场销售某种冰箱，每台进货价为2500元。市场调研表明：当销售价为2900元时，平均每天能售出8台；而当销售价每降低50元时，平均每天就能多售出4台。商场要想使这种冰箱的销售利润平均每天达到5000元，每台冰箱的降价应为多少元？进价售价销售量每台利润总利润降价前降价后250029008400400×82500未知未知未知5000设每台冰箱降价x

元售价每降低50元多售出4台售价每降低100元多售出4×台售价每降低x

元多售出4×台2900-x8+4×400-x例2新华商场销售某种冰箱，每台进货价为2500元。市场调研表明：当销售价为2900元时，平均每天能售出8台；而当销售价每降低50元时，平均每天就能多售出4台。商场要想使这种冰箱的销售利润平均每天达到5000元，每台冰箱的降价应为多少元？解：设每台冰箱降价x

元，根据题意，得8+4×(2900-x

-2500)()=5000解这个方程，得x1=x2=150.2900-150=2750所以，每台冰箱应定价为2750元.某商场将进货价为30元的台灯以40元售出，平均每月能售出600个。调查发现：售价在40元至60元范围内，这种台灯的售价每上涨1元，其销售量就将减少10个.为了实现平均每月10000元的销售利润，这种台灯的售价应定为多少？这时应购进台灯多少个？解：设这种台灯售价上涨x

元，根据题意，得(40+x-30)(600-10x)=10000解这个方程，得x1=10.

x2=40（舍）.售价为：40+x=40+10=50（元）应购置台灯：600-10x=600-10×10=500（个）利用方程解决实际问题得关键和步骤是什么？关键：寻找等量关系步骤：其一是整体地、系统地审清问题；其二是把握问题中的“相等关系”；其三是正确求解方程并检验解的合理性。随堂练习【选自教材P55随堂练习】某批发市场礼品柜台春节期间购进大量贺年卡，一种贺年卡平均每天可售出500张，每张赢利0.3元.为了尽快减少库存，摊主决定采取适当的降价措施.调查发现，如果这种贺年卡的售价每降价0.05元，那么平均每天可多售出200张.摊主要想平均每天赢利180元，每张贺年卡应降价多少元？解:设每张贺卡应降价x

元．(0.3－x)(×200＋500)＝180，解得x1＝0.1，x2＝．又∵摊主想尽快减少库存．∴减得越多,卖得越多．在盈利相同的情况下选择降价0.1元更合适．达标检测【选自教材P55习题2.10】某种服装，平均每天可销售20件，每件赢利44元.在每件降价幅度不超过10元的情况下，若每件降价1元，则每天可多售5件.如果每天要赢利1600元，每件应降价多少元？解:设每件应降价x

元．(5x＋20)(44－x)＝1600，解得:x1＝4，x2＝36(舍去)所以，每件应降价4元．一个农业合作社以64000元的成本收获了某种农产品80t，目前可以以1200元/t的价格售出．如果储藏起来，每星期会损失2t，且每星期需支付各种费用1600元，但同时每星期每吨的价格将上涨200元.那么，储藏多少个星期出售这批农产品可获利122000元？【选自教材P55习题2.10】解:设储藏x个星期出售这批农产