第五章2　平行四边形的判定第1课时课件数学八年级上册

2平行四边形的判定第1课时基础

主干落实重点

典例研析素养

当堂测评基础

主干落实判定平行四边形的方法:(1)两组对边分别__________的四边形是平行四边形;

(2)两组对边分别__________的四边形是平行四边形;

(3)一组对边________________的四边形是平行四边形.

判一判:1.一组对边相等,另一组对边平行的四边形是平行四边形.

()2.两组对角分别相等的四边形是平行四边形.

()

平行

相等

平行且相等

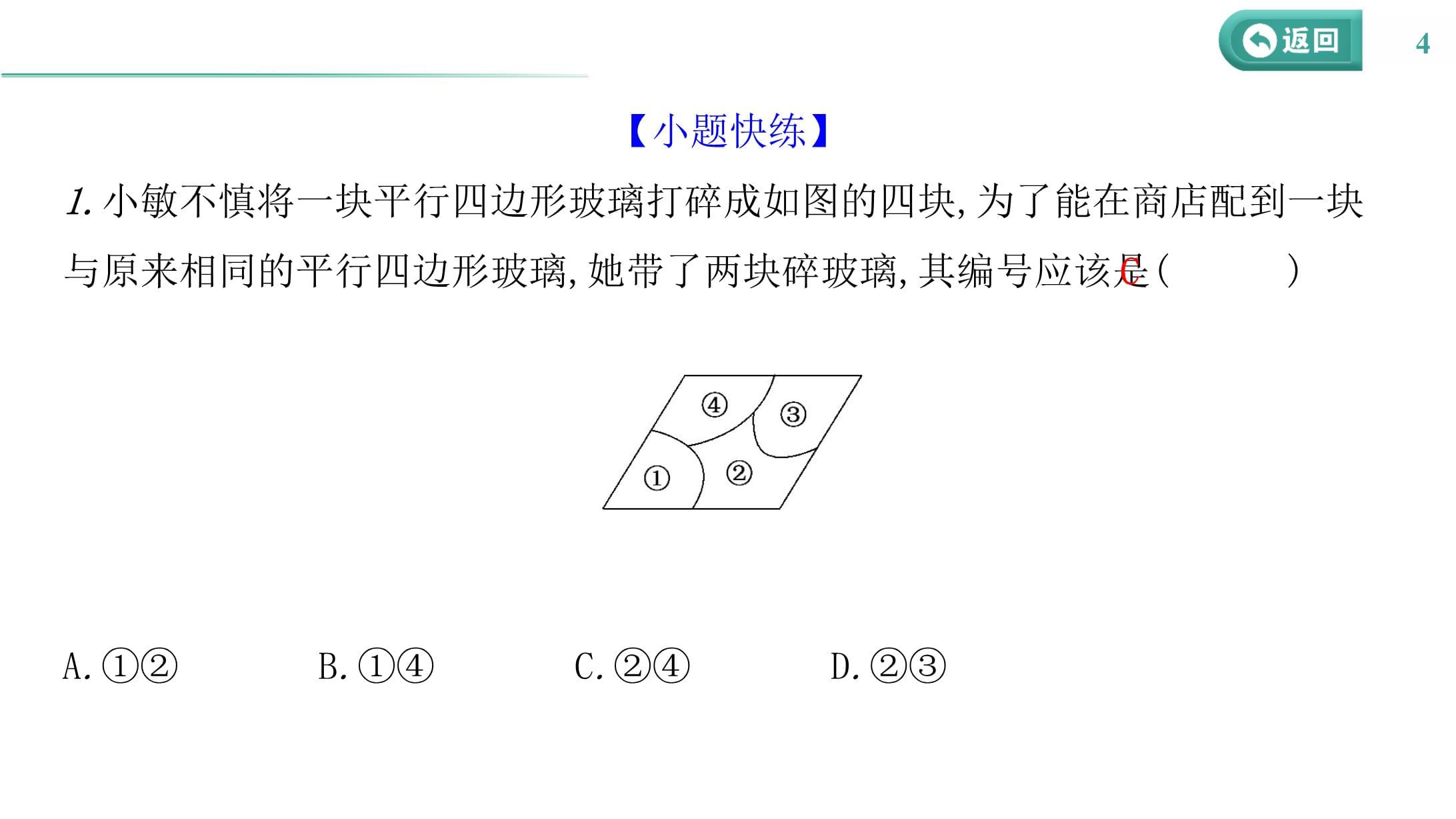
×√【小题快练】1.小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,她带了两块碎玻璃,其编号应该是()A.①②

B.①④

C.②④

D.②③C2.在四边形ABCD中,若AD=8,AB=4,那么当BC=_______,CD=_______时,四边形ABCD是平行四边形.

3.在四边形ABCD中,AB∥CD,AB=8.要使四边形ABCD是平行四边形,则CD的长为_______.

8

4

8

重点

典例研析重点1两组对边分别相等的四边形是平行四边形【典例1】(教材再开发·P128例1拓展)已知:如图,在▱ABCD中,E,F分别是AB,CD的中点.求证:(1)△AFD≌△CEB;

【典例1】(教材再开发·P128例1拓展)已知:如图,在▱ABCD中,E,F分别是AB,CD的中点.(2)四边形AECF是平行四边形.[自主解答](2)由(1)知AE=CF,△AFD≌△CEB,∴AF=CE,∴四边形AECF是平行四边形.【举一反三】如图,以平行四边形ABCD的边AB,CD为边,作等边△ABE和等边△CDF,连接DE,BF.求证:四边形BFDE是平行四边形.

【技法点拨】从两边的角度证明平行四边形的方法(1)两组对边分别平行的四边形是平行四边形.(2)两组对边分别相等的四边形是平行四边形.重点2一组对边平行且相等的四边形是平行四边形【典例2】已知:如图,在平行四边形ABCD中,点M,N分别在AD和BC上,点E,F在BD上,且DM=BN,DF=BE.求证:四边形MENF是平行四边形.

【举一反三】1.依据所标数据,一定为平行四边形的是()B2.如图,E,F是四边形ABCD的对角线AC上两点,AF=CE,DF=BE,DF∥BE.

2.如图,E,F是四边形ABCD的对角线AC上两点,AF=CE,DF=BE,DF∥BE.(2)四边形ABCD是平行四边形.【证明】(2)由(1)知△CFD≌△AEB,∴∠DCF=∠BAE,DC=AB,∴DC∥AB.∴四边形ABCD是平行四边形.素养

当堂测评1.(4分·几何直观、推理能力)(2023·邵阳中考)如图,在四边形ABCD中,AB∥CD,若添加一个条件,使四边形ABCD为平行四边形,则下列正确的是

()A.AD=BC

B.∠ABD=∠BDCC.AB=AD

D.∠A=∠CD2.(4分·几何直观、推理能力)如图,在四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为点E,F.请你只添加一个条件(不另加辅助线),使得四边形AECF为平行四边形,你添加的条件是_______________________.

AE=CF(答案不唯一)

3.(7分·几何直观、推理能力)如图,在▱ABCD中.(2)若BE平分∠ABC且交边AD于点E,AB=5,BC=9,求DE的长.【解析】(2)∵AD∥BC,∴∠AEB=∠CBE