河北省秦皇岛卢龙县联考2024年中考猜题数学试卷含解析

河北省秦皇岛卢龙县联考2024年中考猜题数学试卷

注意事项：

1.答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再

选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

3.考试结束后，将本试卷和答题卡一并交回。

一、选择题（本大题共12个小题，每小题4分，共48分.在每小题给出的四个选项中，只有一项是符合题目要求的.）

1.把一副三角板如图（1）放置，其中NACB=NDEC=90。，NA=41。，/D=30。，斜边AB=4,CD=L把三角

板DCE绕着点C顺时针旋转11。得到△DiCEi（如图2）,此时AB与CDi交于点O,则线段ADi的长度为（）

A.V13B.75C.2夜D.4

2.在如图所示的数轴上，点B与点C关于点A对称，A、B两点对应的实数分别是⑺和-1，则点C所对应的实数

是（）

BAC

II■I,

-1043

A.1+73B.2+73C.273-1D.273+1

3.如图，在正方形ABCD中，点E,F分别在BC,CD±,AE=AF,AC与EF相交于点G,下列结论：①AC垂

直平分EF；②BE+DF=EF；③当NDAF=15。时，△AEF为等边三角形；④当NEAF=60。时，SAABE=-SACEF,其

2

中正确的是（）

A.①③B.②④C.①③④D.②③④

4.如图，矩形ABCD中，AB=3,AD=4,连接BD,NDBC的角平分线BE交DC于点E,现把△BCE绕点B逆时

针旋转，记旋转后的△BCE为ABCE，.当线段BE，和线段B。都与线段AD相交时，设交点分别为F,G.若△BFD

为等腰三角形，则线段DG长为（）

E'

252498

A.—B.—C.—D.一

131355

5.一辆客车从甲地开往乙地，一辆出租车从乙地开往甲地，两车同时出发,它们离甲地的路程y(km)与客车行驶

时间x(h)间的函数关系如图，下列信息：

(1)出租车的速度为100千米/时；

(2)客车的速度为60千米/时；

(3)两车相遇时，客车行驶了3.75小」时；

(4)相遇时，出租车离甲地的路程为225千米.

其中正确的个数有()

—客车一出租车

600卜/

~0\610

A.1个B.2个C.3个D.4个

6.如图，平行四边形ABCD中，E为BC边上一点,以AE为边作正方形AEFG,若ZBAE=4Q°,ZCEF=15°,

则ND的度数是

Brr

A.65°B.55°C.70°D.75°

7.一次函数丫=1«-1的图象经过点P,且y的值随x值的增大而增大,则点P的坐标可以为()

A.(-5,3)B.(1,-3)C.(2,2)D.(5,-1)

8.如图，在四边形ABCD中，对角线AC±BD,垂足为O,点E、F、＜G、H分另()为边AD、AB、BC、CD的中点.若

AC=10,BD=6,则四边形EFGH的面积为()

A.20B.15C.30D.60

2x-a>0

9.如果关于x的不等式组9,八的整数解仅有x=2、x=3,那么适合这个不等式组的整数。、b组成的有序

3x-b<0

数对（a,勿共有。

A.3个B.4个C.5个D.6个

11.一枚质地均匀的骰子，骰子的六个面上分别刻有1到6的点数，投掷这样的骰子一次，向上一面点数是偶数的结

果有（）

A.1种B.2种C.3种D.6种

12.如图，△OAC和△BAD都是等腰直角三角形，ZACO=ZADB=90°,反比例函数y=9在第一象限的图象经过点

x

B,则小OAC与4BAD的面积之差SAOAC-SABAD为（）

二、填空题：（本大题共6个小题，每小题4分，共24分.）

13.如图是抛物线型拱桥，当拱顶离水面2m时，水面宽4Hz.水面下降2.5机，水面宽度增加1

14.在平面直角坐标系中，若点P（2x+6,5x）在第四象限，则x的取值范围是

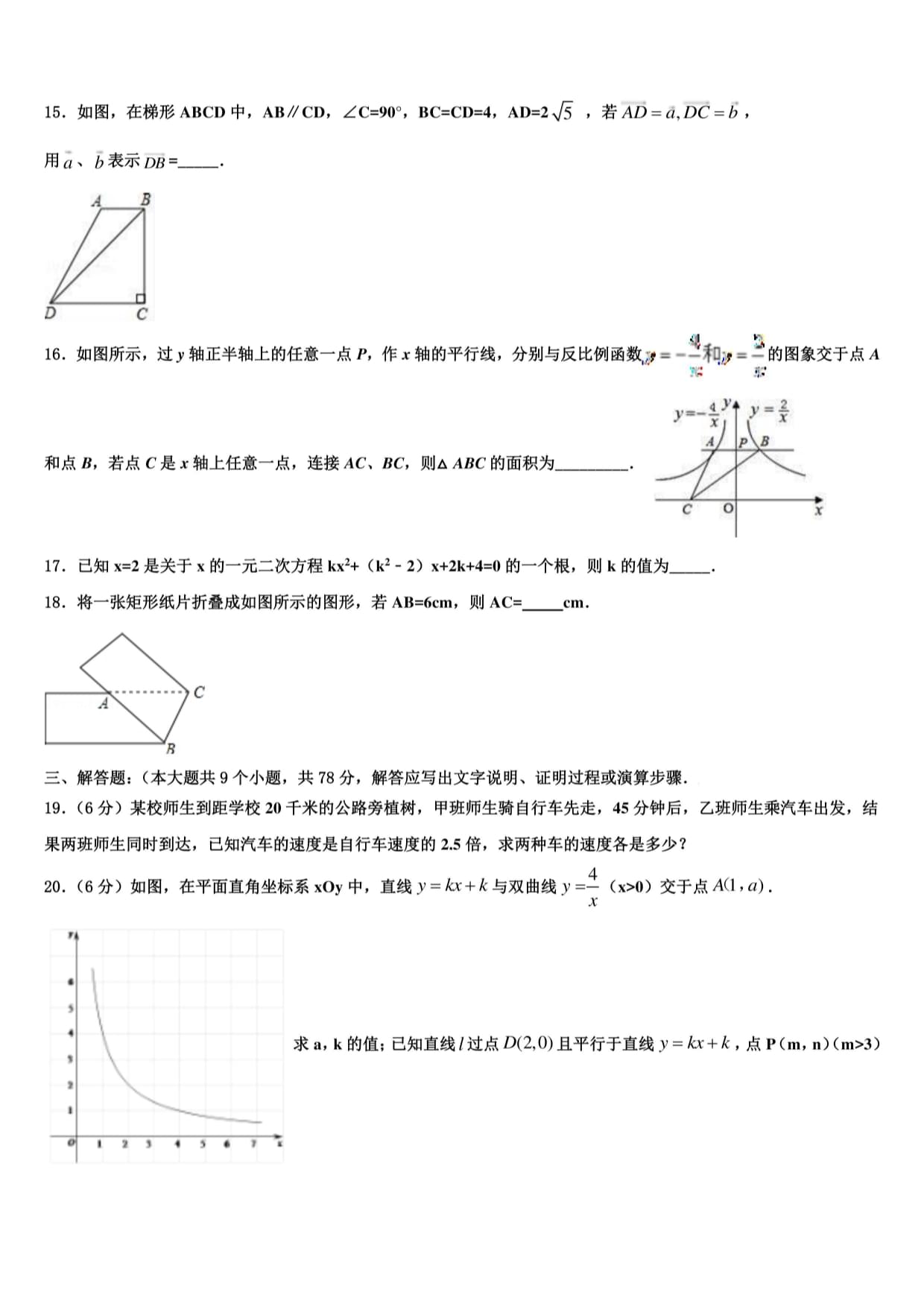
15.如图，在梯形ABCD中，AB〃CD,ZC=90°,BC=CD=4,AD=2逐，若AZ)=a,Z)C=6,

16.如图所示，过y轴正半轴上的任意一点P,作x轴的平行线，分别与反比例函数d=」和孑=二的图象交于点A

和点5,若点C是x轴上任意一点，连接ACBC,则AA3C的面积为

17.已知x=2是关于x的一元二次方程kx?+(k2-2)x+2k+4=0的一个根，则k的值为

18.将一张矩形纸片折叠成如图所示的图形，若AB=6cm,则AC=cm.

三、解答题：(本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤.

19.(6分)某校师生到距学校20千米的公路旁植树，甲班师生骑自行车先走，45分钟后，乙班师生乘汽车出发，结

果两班师生同时到达，已知汽车的速度是自行车速度的2.5倍，求两种车的速度各是多少？

4

20.(6分)如图，在平面直角坐标系xOy中，直线y=履+左与双曲线y=—(x>0)交于点A(l，a).

x

求a,k的值；已知直线/过点。(2,0)且平行于直线y=H+左，点P(m,n)(m>3)

4

是直线/上一动点，过点P分别作X轴、V轴的平行线，交双曲线y=—（x>0）于点M、N,双曲线在点M、NN

间的部分与线段PM、PN所围成的区域（不含边界）记为W.横、纵坐标都是整数的点叫做整点.

①当〃2=4时，直接写出区域W内的整点个数；②若区域W内的整点个数不超过8个，结合图象，求m的取值范围.

21.（6分）计算：|-2|+7+（2017-n）0-4cos45°

22.（8分）如图，在边长为1的小正方形组成的方格纸上，将△ABC绕着点A顺时针旋转90。

画出旋转之后的4AB，。；求线段AC旋转过程中扫过的扇形的面积.

23.（8分）在阳光体育活动时间，小亮、小莹、小芳和大刚到学校乒乓球室打乒乓球，当时只有一副空球桌，他们只

能选两人打第一场.

（1）如果确定小亮打第一场，再从其余三人中随机选取一人打第一场，求恰好选中大刚的概率；

（2）如果确定小亮做裁判，用“手心、手背”的方法决定其余三人哪两人打第一场.游戏规则是：三人同时伸“手心、

手背”中的一种手势，如果恰好有两人伸出的手势相同，那么这两人上场，否则重新开始，这三人伸出“手心”或“手背”

都是随机的，请用画树状图的方法求小莹和小芳打第一场的概率.

24.（10分）如图，海中有一个小岛A,该岛四周11海里范围内有暗礁.有一货轮在海面上由西向正东方向航行，

到达B处时它在小岛南偏西60。的方向上，再往正东方向行驶10海里后恰好到达小岛南偏西45。方向上的点C处.问：

如果货轮继续向正东方向航行，是否会有触礁的危险？（参考数据：72=1-41,若M.73）

25.（10分）如图，AB是。。的直径，CD与。O相切于点C,与AB的延长线交于D.

（1）求证：AADC^>ACDB；

3

（2）若AC=2,AB=-CD,求。O半径.

2

26.（12分）如图，已知△ABC,按如下步骤作图:

①分别以A、C为圆心，以大于.AC的长为半径在AC两边作弧，交于两点M、N；

②连接MN,分另校AB、AC于点D、O；

③过C作CE〃AB交MN于点E,连接AE、CD.

(1)求证：四边形ADCE是菱形;

(2)当NACB=90。，BC=6,AADC的周长为18时，求四边形ADCE的面积.

27.(12分)今年3月12日植树节期间，学校预购进A、B两种树苗，若购进A种树苗3棵，B种树苗5棵,

需2100元，若购进A种树苗4棵，B种树苗10棵，需3800元.

(1)求购进A、B两种树苗的单价；

(2)若该单位准备用不多于8000元的钱购进这两种树苗共30棵，求A种树苗至少需购进多少棵？

参考答案

一、选择题(本大题共12个小题，每小题4分，共48分.在每小题给出的四个选项中，只有一项是符合题目要求的.)

1、A

【解析】

试题分析：由题意易知：ZCAB=41°,ZACD=30°.

若旋转角度为11°,则/A(：0=30。+11。=41。.

:.ZAOC=1800-ZACO-ZCAO=90°.

在等腰RtAABC中，AB=4,贝！|AO=OC=2.

在RtZkAODi中，ODi=CDi-OC=3,

由勾股定理得：AD产而.

故选A.

考点：1.旋转；2.勾股定理.

2、D

【解析】

设点C所对应的实数是x.根据中心对称的性质，对称点到对称中心的距离相等，则有

x--\/3=-^3—(―1^,解得x=2^/§+l.

故选D.

3、C

【解析】

①通过条件可以得出△ABEgAADF,从而得出NBAE=NDAF,BE=DF,由正方形的性质就可以得出EC=FC,就可

以得出AC垂直平分EF,

②设BC=a,CE=y,由勾股定理就可以得出EF与x、y的关系，表示出BE与EF,即可判断BE+DF与EF关系不确

定；

③当NDAF=15。时，可计算出NEAF=60。，即可判断△EAF为等边三角形，

④当NEAF=60。时，设EC=x,BE=y,由勾股定理就可以得出x与y的关系，表示出BE与EF,利用三角形的面积公

式分别表示出SACEF和SAABE,再通过比较大小就可以得出结论.

【详解】

①四边形ABCD是正方形，

；.AB=AD,NB=ND=90°.

在RtAABE和RtAADF中,

AE=AF

AB=AD'

ARtAABE^RtAADF(HL),

；.BE=DF

VBC=CD,

.,.BC-BE=CD-DF,即CE=CF,

VAE=AF,

；.AC垂直平分EF.(故①正确).

②设BC=a,CE=y,

,\BE+DF=2(a-y)

EF=J^y,

...BE+DF与EF关系不确定，只有当y=(2-72)a时成立，(故②错误).

③当/DAF=15。时，

VRtAABE^RtAADF,

.,.ZDAF=ZBAE=15°,

，ZEAF=90°-2xl5°=60°,

又；AE=AF

.•.△AEF为等边三角形.(故③正确).

④当NEAF=60。时，设EC=x,BE=y,由勾股定理就可以得出：

(x+y)2+y2=(72x)2

/.x2=2y(x+y)

1,1

,•SACEF=-x2,SAABE=yy(x+y),

SAABE=—SACEF.(故④正确).

2

综上所述，正确的有①③④，

故选C.

【点睛】

本题考查了正方形的性质的运用，全等三角形的判定及性质的运用，勾股定理的运用，等边三角形的性质的运用，三

角形的面积公式的运用，解答本题时运用勾股定理的性质解题时关键.

4、A

【解析】

25257

先在RtAABD中利用勾股定理求出BD=5,在RtAABF中利用勾股定理求出BF=一,贝|)AF=4--再过G作

888

25

GH〃BF,交BD于H,证明GH=GD,BH=GH,设DG=GH=BH=x,则FG=FD-GD=--x,HD=5-x,由GH〃FB,

8

.FDBDnr—>>45

得出而=而'即可求解.

【详解】

解：在RtAABD中，・.・NA=90。，AB=3,AD=4,

.\BD=5,

在RSABF中，；NA=90°,AB=3,AF=4-DF=4-BF,

/.BF2=32+(4-BF)2,

»25

解得BF=—,

o

257

・・AF=4--=­・

88

过G作GH〃BF,交BD于H,

.\ZFBD=ZGHD,ZBGH=ZFBG,

VFB=FD,

.\ZFBD=ZFDB,

AZFDB=ZGHD,

Z.GH=GD,

111

VZFBG=ZEBC=-ZDBC=-ZADB=-ZFBD,

222

又TNFBG二NBGH,ZFBG=ZGBH,

ABH=GH,

25

设DG=GH=BH=x,贝!JFG=FD・GD二一-x,HD=5-x,

8

VGH/7FB,

.FDBD—5

•.---=----，即nn8=------

GDHD—5-x

x

25

解得X==.

13

故选A.

【点睛】

本题考查了旋转的性质，矩形的性质，等腰三角形的性质，勾股定理，平行线分线段成比例定理，准确作出辅助线是

解题关键.

5、D

【解析】

根据题意和函数图象中的数据可以判断各个小题是否正确，从而可以解答本题.

【详解】

由图象可得，

出租车的速度为：600+6=100千米/时，故（1）正确，

客车的速度为：600+10=60千米/时，故（2）正确，

两车相遇时，客车行驶时间为：600+（100+60）=3.75（小时），故（3）正确，

相遇时，出租车离甲地的路程为：60x3.75=225千米，故（4）正确，

故选D.

【点睛】

本题考查一次函数的应用，解答本题的关键是明确题意，利用数形结合的思想解答.

6、A

【解析】

分析：首先求出NAEB,再利用三角形内角和定理求出NB,最后利用平行四边形的性质得ND=NB即可解决问题.

详解：•.•四边形ABCD是正方形，

/.ZAEF=90o,

,.,ZCEF=15°,

，ZAEB=180o-90°-15o=75°,

,.•ZB=180°-ZBAE-ZAEB=180o-40o-75o=65°,

•••四边形ABCD是平行四边形，

ZD=ZB=65°

故选A.

点睛：本题考查正方形的性质、平行四边形的性质、三角形内角和定理等知识，解题的关键是灵活运用所学知识解决

问题，学会用转化的思想思考问题，属于中考常考题型.

7、C

【解析】

【分析】根据函数图象的性质判断系数k>0,则该函数图象经过第一、三象限，由函数图象与y轴交于负半轴，则该

函数图象经过第一、三、四象限，由此得到结论.

【详解】•••一次函数y=kx-1的图象的y的值随x值的增大而增大，

.,.k>0,

,4一一,

A、把点（-5,3）代入y=kx-1得至！J：k=-y<0,不符合题意；

B、把点（1,-3）代入y=kx-1得至U：k=-2<0,不符合题意；

.,一一3.,

C、把点(2,2)代入y=kx-l得到：k=—>0,符合题意；

D、把点(5,-1)代入y=kx-1得至!］：k=0,不符合题意，

故选C.

【点睛】考查了一次函数图象上点的坐标特征，一次函数的性质，根据题意求得k>0是解题的关键.

8、B

【解析】

有一个角是直角的平行四边形是矩形.利用中位线定理可得出四边形EFGH是矩形，根据矩形的面积公式解答即可.

【详解】

•.•点E、F分别为四边形ABCD的边AD、AB的中点，

)1

.,.EF#BD,且EF=-BD=L

2

同理求得EH〃AC〃GF,且EH=GF=^AC=5,

2

又；AC_LBD,

，EF〃GH,FG〃HE且EF_LFG.

四边形EFGH是矩形.

/.四边形EFGH的面积=EF・EH=1X5=2,即四边形EFGH的面积是2.

故选B.

【点睛】

本题考查的是中点四边形.解题时，利用了矩形的判定以及矩形的定理，矩形的判定定理有：

(1)有一个角是直角的平行四边形是矩形；

(2)有三个角是直角的四边形是矩形；

(1)对角线互相平分且相等的四边形是矩形.

9、D

【解析】

nh

求出不等式组的解集，根据已知求出1<—及、3<-<4,求出2<aW4、9<b<12,即可得出答案.

23

【详解】

解不等式2x-aK),得：x>-,

2

b

解不等式3x-bW0,得：x<-,

•.•不等式组的整数解仅有x=2、x=3,

r、ab

则l<-<2,3<-<4,

23

解得：2Va*、9<b<12,

则a=3时，b=9、10、11；

当a=4时,b=9、10、11；

所以适合这个不等式组的整数a、b组成的有序数对（a,b）共有6个，

故选：D.

【点睛】

本题考查了解一元一次不等式组，不等式组的整数解，有序实数对的应用，解此题的根据是求出a、b的值.

10、B

【解析】

分析：根据三角形全等的判定方法得出乙和丙与△ABC全等，甲与AABC不全等.

详解：乙和AABC全等；理由如下：

在△ABC和图乙的三角形中，满足三角形全等的判定方法：SAS,

所以乙和△ABC全等；

在△ABC和图丙的三角形中，满足三角形全等的判定方法：AAS,

所以丙和△ABC全等；

不能判定甲与△ABC全等；

故选B.

点睛：本题考查了三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS,HL.注意:

AAA,SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须

是两边的夹角.

11、C

【解析】

试题分析：一枚质地均匀的正方体骰子的六个面上分别刻有1到6的点数，掷一次这枚骰子，向上的一面的点数为偶

数的有3种情况，故选C.

考点：正方体相对两个面上的文字.

12、D

【解析】

设AOAC和△R4O的直角边长分别为a、b,结合等腰直角三角形的性质及图象可得出点5的坐标，根据三角形的面

积公式结合反比例函数系数k的几何意义以及点B的坐标即可得出结论.

解：设4。4。和4BAD的直角边长分别为a、b,

则点5的坐标为（4+方，a-b）.

・；点B在反比例函数y=-的第一象限图象上,

:.（a+b）x（Q-））=a2-b2=l.

1。1。1/。八1

*••SAOAC~BAD--a2--b2=-（，-〃）_xi=2.

222=2

故选D.

点睛：本题主要考查了反比例函数系数上的几何意义、等腰三角形的性质以及面积公式，解题的关键是找出4-"的

值.解决该题型题目时，要设出等腰直角三角形的直角边并表示出面积，再用其表示出反比例函数上点的坐标是关键.

二、填空题：（本大题共6个小题，每小题4分，共24分.）

13、1.

【解析】

根据已知建立平面直角坐标系，进而求出二次函数解析式，再通过把y=-L5代入抛物线解析式得出水面宽度，即可得

出答案

【详解】

解：建立平面直角坐标系，设横轴x通过AB,纵轴y通过AB中点O且通过C点，则通过画图可得知O为原点，

抛物线以y轴为对称轴，且经过A,B两点，OA和OB可求出为AB的一半1米，抛物线顶点C坐标为（0,1）,

设顶点式丫=@*】+1,把A点坐标（-1,0）代入得a=-0.5,

.••抛物线解析式为y=-0.5xi+l,

当水面下降1.5米，通过抛物线在图上的观察可转化为：

当y=15时，对应的抛物线上两点之间的距离，也就是直线y=-l与抛物线相交的两点之间的距离，

可以通过把y=-1.5代入抛物线解析式得出：

-1.5=-0.5xi+L

解得：x=±3,

lx3-4=l,

所以水面下降1.5m,水面宽度增加1米.

故答案为1.

【点睛】

本题考查了二次函数的应用，根据已知建立坐标系从而得出二次函数解析式是解决问题的关键，学会把实际问题转化

为二次函数，利用二次函数的性质解决问题，属于中考常考题型.

14、-3<x<l

【解析】

根据第四象限内横坐标为正，纵坐标为负可得出答案.

【详解】

:点P(2x-6,x-5)在第四象限，

(22-6>0

I5二V?

解得-3VxVl.故答案为-3VxVL

【点睛】

本题考查了点的坐标、一元一次不等式组，解题的关键是知道平面直角坐标系中第四象限横、纵坐标的符号.

1

15、一b—a

2

【解析】

过点A作AELDC,利用向量知识解题.

【详解】

解：过点A作AELDC于E,

VAE±DC,BC±DC,

，AE〃BC,

XVAB//CD,

二四边形AECB是矩形，

；.AB=EC,AE=BC=4,

•*-DE=飞AD?-AE?={(2布)--42=2,

1

；.AB=EC=2=—DC,

2

DC=b，

:.AB=-b,

2

AD=a，

DA=—d，

:.DB=DA+AB=—aH—b,

【点睛】

向量知识只有使用沪教版(上海)教材的学生才学过，全国绝大部分地区将向量放在高中阶段学习.

16、1.

【解析】

设P(0,b),

•.•直线APB〃x轴，

:.A,B两点的纵坐标都为b,

4

而点A在反比例函数y=--的图象上，

x

：9y=b,X=-y,即A点坐标为(J,b),

bb

2

又•・•点B在反比例函数y=一的图象上，

x

?9

・••当y=b,x=-,即B点坐标为(：，b),

bb

・116

・・SAABC=—•AB*OP=—•—*b=l.

22b

17、-1

【解析】【分析】把x=2代入kx2+(k2-2)x+2k+4=0得4k+2k2-4+2k+4=0,再解关于k的方程，然后根据一元二次

方程的定义确定k的值即可.

【详解】把x=2代入kx2+(k2-2)x+2k+4=0得4k+2k2-4+2k+4=0,

整理得k2+lk=0,解得ki=O,ki=-1,

因为呼0,

所以k的值为-1.

故答案为：-1.

【点睛】本题考查了一元二次方程的定义以及一元二次方程的解，能使一元二次方程左右两边相等的未知数的值是一

元二次方程的解.

18、1.

【解析】

试题分析：如图，\•矩形的对边平行，.*.Z1=ZACB,VZ1=ZABC,/.ZABC=ZACB,AAC=AB,VAB=lcm,

/.AC=lcm.

考点：1轴对称；2矩形的性质；3等腰三角形.

三、解答题：(本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤.

19、自行车速度为16千米/小时，汽车速度为40千米/小时.

【解析】

设自行车速度为x千米/小时，则汽车速度为2.5x千米/小时，根据甲班师生骑自行车先走，45分钟后，乙班师生乘汽

车出发，结果同时到达，即可列方程求解.

【详解】

设自行车速度为x千米/小时，则汽车速度为2.5x千米/小时，由题意得

2045_20

x602.5%

解得x=16,

经检验x=16适合题意，

2.5x=40,

答：自行车速度为16千米〃J、时，汽车速度为40千米/小时.

20、(1)a=4,k=2；(2)①3,②3<mW4.5.

【解析】

4

(1)将41，。)代入y=—可求出a,将A点坐标代入y=H+左可求出k；

x

(2)①根据题意画出函数图像，可直接写出区域W内的整点个数；

②求出直线/的表达式为y=2x-4,根据图像可得到两种极限情况，求出对应的m的取值范围即可.

【详解】

4

解：(1)将4(1，。)代入y=—得a=4

x

将4(1,4)代入左+左=4,得％=2

(2)①区域W内的整点个数是3

②,:直线I是过点£>(2,0)且平行于直线y=2x+2

二直线/的表达式为y=2x-4

当2光—4=5时，即x=4.5线段PM上有整点

3<m<4.5

【点睛】

本题考查了待定系数法求函数解析式以及函数图像的交点问题，正确理解整点的定义并画出函数图像，运用数形结合

的思想是解题关键.

21、1.

【解析】

直接利用零指数幕的性质以及特殊角的三角函数值和绝对值的性质分别化简得出答案.

【详解】

解：原式=2+2.-4X)

=2+2-+1-2-

=1.

【点睛】

此题主要考查了实数运算，正确化简各数是解题关键.

22、.(1)见解析(2)冗

【解析】

(1)根据网格结构找出点B、C旋转后的对应点B，、C的位置，然后顺次连接即可.

(2)先求出AC的长，再根据扇形的面积公式列式进行计算即可得解.

【详解】

解：(1)△ABC，如图所示：

(2)由图可知，AC=2,

90•-22

二线段AC旋转过程中扫过的扇形的面积=%，=n.

360

23、(1)—(2)—

34

【解析】

(1)由小亮打第一场，再从其余三人中随机选取一人打第一场，求出恰好选中大刚的概率即可；

(2)画树状图得出所有等可能的情况数，找出小莹和小芳伸“手心”或“手背”恰好相同的情况数，即可求出所求的概率.

【详解】

解：(1)•••确定小亮打第一场，

...再从小莹，小芳和大刚中随机选取一人打第一场，恰好选中大刚的概率为:；

(2)列表如下：

所有等可能的情况有8种，其中小莹和小芳伸“手心”或“手背”恰好相同且与大刚不同的结果有2个,

21

则小莹与小芳打第一场的概率为二=-.

84

【点睛】

本题主要考查了列表法与树状图法；概率公式.

24、不会有触礁的危险,理由见解析.

【解析】

BH

分析：作AH_LBC,由NCAH=45。，可设根据=----可得关于x的方程，解之可得.

AH

详解：过点A作A77LBC,垂足为点〃.

由题意，得N5AH=60。，ZCAH=45°,BC=1.

设AH=x,则CH=x.

在RtAABH中，tanZBAH=tan60°=1°十苫，:.>j3x=10+x,

AHx

解得：X=5A/3+5^13.65.

；13.65>11,.•.货轮继续向正东方向航行，不会有触礁的危险.

点睛：本题考查了解直角三角形的应用-方向角问题，解一般三角形的问题一般可以转化为解直角三角形的问题，解

决的方法就是作高线.

25、(1)见解析；(2)6

2

【解析】

分析：(1)首先连接CO,根据CD与。O相切于点C,可得:NOCD=90°；然后根据AB是圆O的直径，可得:ZACB=90°,

据此判断出NCAD=/BCD,即可推得4ADC^ACDB.

(2)首先设CD为x,则AB=32x,OC=OB=34x,用x表示出OD、BD；然后根据小ADC^ACDB,可得:ACCB=CDBD,

据此求出CB的值是多少，即可求出。O半径是多少.

详解：

(1)证明：如图，连接CO,

「CD与OO相切于点C,

.\ZOCD=90°,

TAB是圆O的直径,

NACB=90。，

.♦.NACOh/BCD,

,-,ZACO=ZCAD,

.,.ZCAD=ZBCD,

在AADC^ACDB中，

ZCAD=/BCD

ZADC=ZCDB

/.△ADC^ACDB.

(2)解：设CD为x,

33

贝！|AB=-x,OC=OB=-x,

24

VZOCD=90°,

0D=7<9C2+CD2=yl(^x)2+x2=：x,

531

・・BD=OD-OB=—x-----x=—x,

442

由(1)知，△ADCs/\CDB,

.ACCD

・・----=-----9

CBBD

2_x

即ZF一厂，

—x

2

解得CB=1,

；•AB=7AC2+BC2=百，

.•.(DO半径是好.

2

点睛