高中数学【立体几何】多选题专项训练

高中数学【立体几何】多选题专项训练

1.如图,正方形ABC。中,E、尸分别是AB、BC的中点将“。EqaJFgBEF分别沿

DE、DF、所折起，使4B、C重合于点尸.则下列结论正确的是

A.PDYEF

B.平面PZ)E_L平面PZ)尸

C.二面角P-E尸-。的余弦值为g

D.点P在平面OE尸上的投影是ADEF的外心

2.如图，在棱长均相等的四棱锥P-ABCD中，。为底面正方形的中心，分别为侧棱

的中点，有下列结论正确的有：

B.平面PC£>〃平面OMN

C.直线尸。与直线MN所成角的大小为90D.ONLPB

3.已知正四棱柱ABC。-A4GA的底面边长为2,侧棱A4,=l,尸为上底面上的

动点，给出下列四个结论中正确结论为()

A.若PD=3,则满足条件的尸点有且只有一个

B.若尸。=6，则点尸的轨迹是一段圆弧

C.若〃平面ACB,,则。P长的最小值为2

D.若尸£>〃平面ACB,,且尸。=后，则平面30P截正四棱柱ABCD-AB©。的外接球所

9乃

得平面图形的面积为下

4

4.己知正方体ABCD-ABCQ棱长为2,如图，M为CG上的动点，40，平面a.下面说

法正确的是()

A.直线A8与平面a所成角的正弦值范围为

B.点M与点C1重合时，平面a截正方体所得的截面，其面积越大，周长就越大

C.点M为CC,的中点时，若平面a经过点8,则平面a截正方体所得截面图形是等腰梯形

D.已知N为。。中点，当AM+MN的和最小时，M为CG的中点

答案第2页，共20页

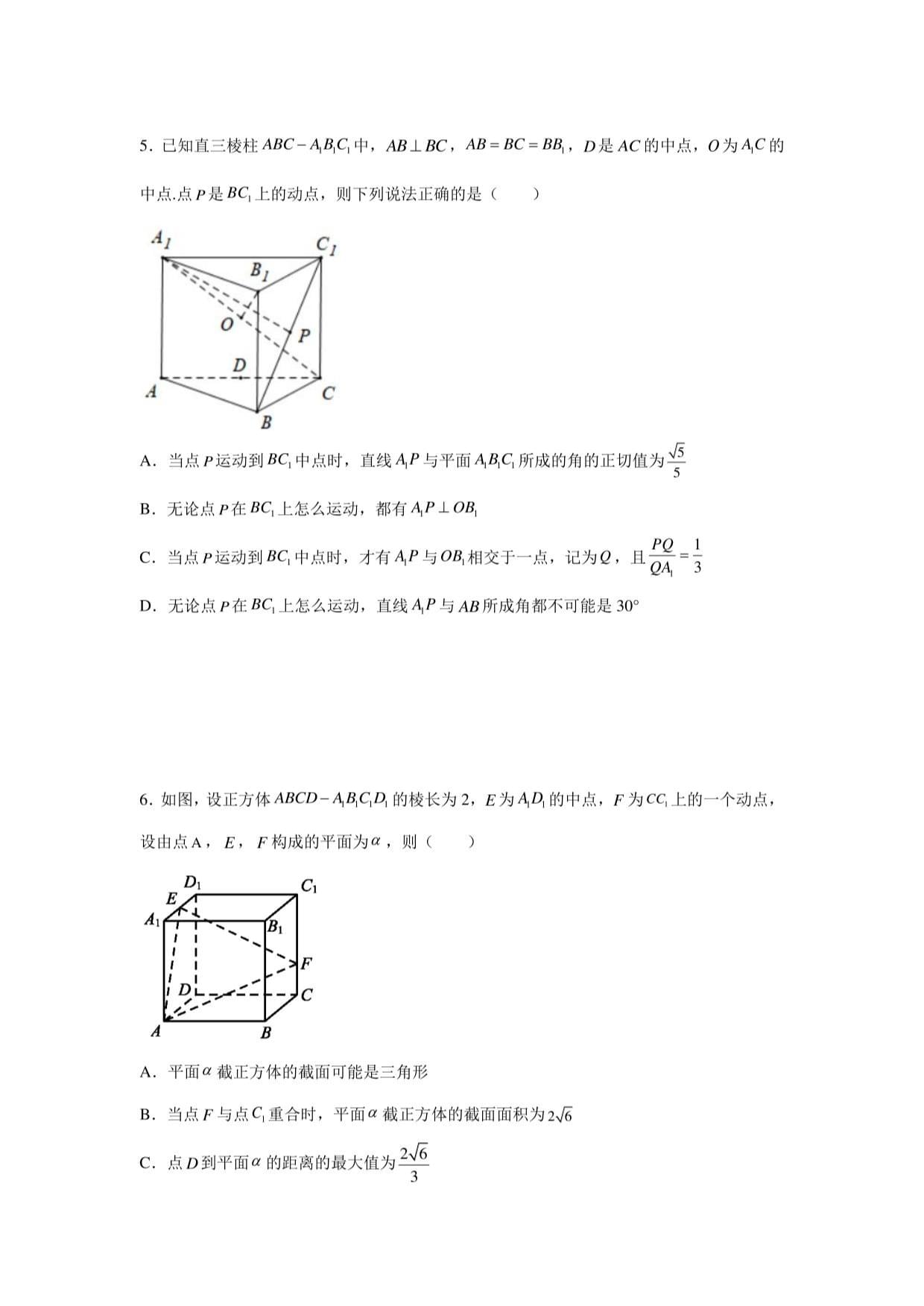
5.已知直三棱柱ABC-AB|G中，ABJ.BC,AB=BC=BB],。是AC的中点，。为AQ的

中点.点P是BG上的动点，则下列说法正确的是(

A.当点尸运动到BG中点时，直线AF与平面AMG所成的角的正切值为手

B.无论点P在BG上怎么运动，都有

C.当点P运动到8G中点时，才有4尸与。耳相交于一点，记为Q,且黑=:

D.无论点尸在BG上怎么运动，直线4P与所成角都不可能是30°

6.如图，设正方体A8CD-A4GQ的棱长为2,E为AA的中点，尸为CG上的一个动点,

设由点A,E,F构成的平面为a,则()

平面&截正方体的截面可能是三角形

当点尸与点G重合时，平面a截正方体的截面面积为

点。到平面a的距离的最大值为亚

3

D.当尸为CG的中点时，平面a截正方体的截面为五边形

7.如图，在棱长为2的正方体ABCD-A'B'C'。中，M为BC边的中点，下列结论正确的有

A.AM与OB所成角的余弦值为巫

10

9

B.过三点A、M、的正方体A8CD—A'8'CZ）'的截面面积为二

2

C.四面体AC8O的内切球的表面积为27T

D.正方体ABCD-AB'C'。'中，点P在底面A'8'C'。'（所在的平面）上运动并且使

ZMAC^ZPAC,那么点尸的轨迹是椭圆

答案第4页，共20页

寿光现代中学强基年级2019级立体几何多选题专项训练2

命题人：陈飞审题人：桑培祥

8.《九章算术》中将底面为直角三角形且侧棱垂直于底面的三棱柱称为“堑堵”:底面为矩形,

一条侧棱垂直于底面的四棱锥称之为“阳马”；四个面均为直角三角形的四面体称为“鳖牖

如图在堑堵ABC-421G中，ACLBC,且4h=AB=2.下列说法正确的是

A.四棱锥8-4ACG为“阳马”

B.四面体4cle8为“鳖膈”

2

C.四棱锥B-4ACG体积最大为］

D.过A点分别作于点E,AFL4C于点凡则EFLAB

9.如图四棱锥P-43CD,平面平面ABCD,侧面PAO是边长为2遥的正三角形,

底面ABC。为矩形，CD=2B点。是PO的中点，则下列结论正确的是（）

A.CQ_L平面尸AQ

B.PC与平面AQC所成角的余弦值为逑

3

C.三棱锥B-ACQ的体积为6及

D.四棱锥Q-ABC。外接球的内接正四面体的表面积为24行

10.如图，线段AB为圆。的直径，点E,尸在圆。上，EF//AB,矩形A8C。所在平面和

圆。所在平面垂直，且43=2,EF=AD=1,则下述正确的是（）

A.0尸//平面

B.平面A£）F

C.点A到平面C。/花的距离为亘

7

D.三棱锥C-BEF外接球的体积为&

11.在正方体中，AB=4,E,F分别为8耳,CD的中点，P是上的动

A.AFJ•平面ARE

答案第6页，共20页

B.平面ARE截正方体ABC。-AgGR的截面面积为18

C.三棱锥ARE的体积与p点的位置有关

D.过AE作正方体ABCO-agCQ的外接球的截面，所得截面圆的面积的最小值为5万

12.为弘扬中华民族优秀传统文化，某学校组织了《诵经典，获新知》的演讲比赛，本次比

赛的冠军奖杯由一个铜球和一个托盘组成，如图①，已知球的体积为手，托盘由边长为4

的正三角形铜片沿各边中点的连线垂直向上折叠而成，如图②.则下列结论正确的是（）

A.经过三个顶点A,B,C的球的截面圆的面积为；

B.异面直线AD与CF所成的角的余弦值为（

O

TT

C.直线AO与平面DE尸所成的角为H

D.球离球托底面。环的最小距离为百+日-1

13.已知直三棱柱A8C-A4G中，ABLBC,AB=BC=BB。。为4（的中点.点P满足

BP=^BC,其中&[0川,则()

A.对时，都有4尸_1_。耳

B.当4时，直线47与A8所成的角是30°

C.当a=；时，直线AP与平面A&G所成的角的正切值手

1PQ1

D.当义=:时，直线AP与。用相交于一点。，则言二不

14.在菱形ABCD中，AB=2,NA8C=60。，将菱形4BC£＞沿对角线AC折成大小为

。（。£（0。,180。））的二面角8—47—。，四面体A3CD内接于球。，下列说法正确的是（）

A.四面体A3CO的体积的最大值是1

B.四面体A8CO的表面积的最大值是4+23

C.当6=90。时，A3与CO所成的角是60。

D.当6=60。时，球O的体积为经叵

81

15.已知正方体ABCD-ABC。的棱长为2,点E,F在平面A8CR内，若|AE|=VL

AC1DF,则（）

A.点E的轨迹是一个圆

B.点尸的轨迹是一个圆

C.|印的最小值为四一

D.AE与平面48。所成角的正弦值的最大值为当

答案第8页，共20页

参考答案

I.ABC对于A选项，作出图形，取EF中点H,连接PH,DH,又原图知尸和△£＞切为等腰三角形，故

DH工EF，所以EF±平面PDH，所以PDJLEF，故A正确；根据折起前后，可知PE,PF,PD三线两两垂直，

于是可证平面尸DE_1_平面尸，＞尸，故B正确：根据A选项可知NPHD为二面角P—EF—D的平面角，设正方形边

长为2,因此PE=M=I，PH=—.DW=2V2--=—•PD=-JDF2-PF2=2-由余弦定理

222

PH?_J_HD2—p/~)21

得：cosZ.PHD=—-~-=--故c正确：由于PE=PFKPD，故点尸在平面OEF上的投影不

2PH-HD3

是△QEE的外心，即D错误：故答案为ABC.

2.ABD选项A,连接BD,显然0为BD的中点，又N为PB的中点，所以〃0N,由线面平行的判定定理可得，〃平

面OMN；选项B.由A1.N分别为侧棱丛.28的中点.得MN〃AB,又底面为正方形，所以MN〃CD，由线面平行的判定

定理可得，CD〃平面OMN,又选项A得P。〃平面OMN，由面面平行的判定定理可得，平而PCD〃平面OMN；选项

C,因为MN〃CD,所以NPDC为直线尸。与直线MN所成的角，又因为所有校长都相等，所以NPDC=60'，故直线尸。与

直线MN所成角的大小为60」：选项D,因底面为正方形，所以A82+AZJ2=•又所有梭长都相等，所以

PB2+PD2=8£＞2，故PB±PD、又

PD〃GN,所以ON工PB，故ABD均正确.

3.ABD

••,正四棱柱ABCO-ABCQi的底面边长为2,二42=20，又何棱

AA=1,二=J(2及J+『=3,则P与81重合时尸£)=3,此

时P点唯一，故4正确：

•；PO=J§e(l,3)，DDt=1,则PR=0,即点尸的轨迹是一段圆

弧，故B正确:

连接。A-DC、,可得平面A〃G〃平面AC8「则当尸为AG中点时，0P有最小值为=^3，故c

错误;

由c知，平面5OP即为平面,平面截正四棱柱ABCQ-AgGR的外接球所得平面图形为外接球的

大圆，其半径为，"T57仔=3,面积为旦，故。正确.

224

4.AC对于A选项，以点。为坐标原点，D4、DC、所在直线分别为X、y、Z轴

建立空间直角坐标系。一盯z,则点A（2,0,0）、8（2,2,0）、设点

M（0,2,a）（0<a<2）,

平面。，则祝为平面a的一个法向量,且画了=（-2,2,a）,丽=（0,2,0）,

1同〈方祝＞卜1巴竺I尸g也[

|AB|-|AM|2xVa2+8J/+8[32.

所以，直线AB与平面a所成角的正弦值范围为1—.A选项正确：

对于B选项，当M与C£重合时，连接A,。、8£＞、AB、AC，

在正方体ABC。一ABCD中，CG，平面ABC。，（28。（=平面488，，8。_1616,

...四边形ABC。是正方形，则5DJ_AC，•••CGnAC=C,，或）"!"平面4CC「

QACtu平面ACC1，；.AR±BD,同理可证AG1A©.

♦.♦AQcB。=£）,;.AC〕J-平面A/。，

易知AA8。足边长为2夜的等边三角形，其面积为§,、,”0=手X（2j5）2=2，3,周长为20x3=60.

设E、F-。、N、G、”分别为楂AR、44、BB-BC、CD、OR的中点，

易知六边形EFQNGH是边长为&的正六边形，且平面EFQNGHH平面A}BD.

正六边形EFQNGH的周长为675,面积为6x=3-73.

则AA8。的面积小于正六边形EFQNG”的面积，它们的周长相等，B选项错误:

对于c选项，设平面a交棱A,A于点E（。,0,2）.点M（0,2,1）,AM=（-2,2,1）.

AM_L+而a,DEu平而a•AMJ_DE,即AM•DE=—2b+2=0,得6=1,

E（l,0,2）,

所以，点E为棱4。的中点，同理可知，点F为棱Ad的中点，则F（2,l,2）,EF=（l,l,0），

答案第10页，共20页

而丽=（2,2,0）,...乔=g丽，...E/7/D8且所

由空间中两点间的距离公式可得DE=722+02+12=BBF=7（2-2）2+（1-2）2+（2-0）2=J5，

/.DE=BF，

所以，四边形8OEF为等腰梯形，C选项正确；

对于D选项，将矩形ACGA与矩形CGRD延展为一个平面，如下图所示：

若AM+最短，则A、M.N三点共线,

亲离1=2一"

MC=2-4i看gcC、

所以，点用不是棱CR的中点，D选项错误.

5.ABD直三棱柱ABC-A5G中，ABLBC-AB=BC=BBX

选项4中，当点p运动到BQ中点时，有E为B|G的中点，连接AE、EP-如下图示

即有EPJ_而A4G

EP

二直线A7与平面AAG所成的角的正切值:tanZPAE=——

“AE

EP=；BBt.AE=办席+与6=与BBy

•••tanZ?4E=y->故A正确

选项8中，连接BC，与8cl交于E,并连接AB.如下图示

由题意知，B]BCG为正方•形,即有4CJ.8G

而AB_LBC口ABC-A181G为直三棱柱，有A,4_L面gBCC,.BC,u面BtBCCt

；.4旦±BC,,又44ngc=4

BC,±面AqC,0与u面A,B|C,故8C|_LOB、

同理可证：A,8_L081,又ABcBQ=B

J_面ABC1，又A/u面A,BC1,即有故8正确

选项c中，点尸运动到BG中点时，即在AA8c中Af、0B1均为中位线

二。为中位线的交点

PQ1

.,.根据中位线的性质有：—7=^"故C错误

QA2

选项。中，由于A,B1//A8,直线Af与AB所成角即为4月与AP所成角：ZBX\P

结合下图分析知：点户在BG上运动时

当P在8或G上时，/B|AP最大为45°

当p在8G中点上时，ZB^P最小为arctan>arctan43=30°

23

二Z?iAP不可能是30。，故。正确

6.BCD

如图，建立空间直角坐标系，延长AE与z轴交于点p.连接尸尸与y轴交于点儿/.

则平面a由平面AEF扩展为平面APM,由此模型可知A错误，H,。正确.

。（0,0,0）,4（2,0,0）,「（0,0,2）设点加的坐标为（0/。«€[2,4]）,

方=（2,0,0）,而=（-2/,0）.PA=（2,0,-2）

则可知点尸到直线AM的距离为I?=

则可得△APM的面积S=1J产+4-d2=>/5尸+16.

S△弘o=g-2-4=4,设点。到平面a的距离为〃.

利用等体积法VD-APM=XM-MD，即:.'"=g•S&pz/t

»4fh=1-

可得〃=一厂，—・•则I16，

V5r+16/+产

答案第12页，共20页

h二4

由一「16在fe[2,4]单调递增所以当r=4时,力取到最大值为2芈.

7.AB

A：构建如下图所示的空间直角坐标系:

则有：A(0,0,2),M(1,2,2),B'(0,2,0),。'(2,0,0),

•••AW=(1,2,0),=(-2,2,0)，

—-=^；AMD^2Ma”

cos<AM,DB>=.­.=—T=—=-------,故正确.

\AM\\D,B,\yJ5xy/s10

B:若N为CC'的中点，连接MM则有MV//AT>'，如下图示，

・•・梯形AMND'为过三点A、M、D0的正方体ABC。一A3'CZ>'的截面，

而MN=72,AD'=2>/2,AM=D'N=小，可得梯形的高为逑,

2

二梯形的面积为S=1x3j2x£Z=2.故正确.

222

c：如下图知：四而体A'C'B。的体积为正方体体积减去四个直极锥的体积,

।।8

V=8-4x-x-x8=-,而四面体的棱长都为2J5,有表面积为

S=4x1x2^x272xsin-=8^,

23

10八

;若其内切圆半径为r,则有上x8j?-r=-,即r所以内切球的表面积为

333

47r

44，=——.故错误.

3

D：正方体AgCO-A'8'CZ)'中，点尸在底面A'8'CZ)'(所在的平面)上运动且NM4C'=NR4C'，即2的轨迹

为面A'3'C'。'彼以AM、AP为母线，,为轴的圆锥体侧面所得曲线，如下图曲线GPK，

构建如下空间直角坐标系，A(0,0,2),M(-逝，延⑵,C'(0,2&,0)，若尸",%())，则

22

AM=(―-^-，―^―,0),AC=(0,2-\/2,—2),AP=(x,y,—2)•

6岳

cosZMAC=

\AM\\AC\舟疝一5

理整理得

8,如0=迎-f=/,0'+2「，即/,二'+2

IAP\\ACf\旧+/+4X6旧+y2+4

(y+l()J5)2-9x2=216(y>0)，即轨迹为双曲线的一支，故错误.故选：AB

8.ABD底面为直角三角形且侧棱垂直于底面的三棱柱称为“堑堵

所以在堑堵4BC-4SG中，AC1BC,侧棱AA-L平面A8C.

在选项A中.所以AABC,又AC_LBC,且AAnAC=A，则BC_L平面AAGC.

所以四棱锥B-AMCG为“阳马”，故A正确.

在选项B中.由AC_LBC,即AGJ_BC,又4G■1■£(?且C|CnBC=c，所以4GJ■平面88cle.

所以AG，BC-则VA^G为直角三角形.

又由BC_L平面AAGC,得AA|BC为直角三角形.

由“堑堵”的定义可得AA£C为直角三角形，ACGB为直角三角形.

所以四面体4GCB为“鳖瞒”，故B正确.

在选项c中.在底面有4=AC?+8C2Z2AC-3CMAC-BCM2当且仅当AC=8C时取等号.

1124

V»AACC=—S,xBC=—AA,xACxBC=—ACxBC4—，所以c不正确.

34向ex13133

在选项D中.由上面有BC_L平面AAGC，则且ACn8C=C,则AF_L平而\BC

所以AF_LA8AEA.MB且AFcAE=A,则A1J-平面AEF，则AtB1.EF，所以D正确.

9.BD

解：取AO的中点0，BC的中点E，连接OE,OP，

因为三角形PAD为等边三角形，所以OP_LA£>.

因为平面PAD_L平面ABC。，所以OPJ_平面ABCD.

因为AO_LOE，所以0O,0E,0P两两垂直，

所以，如下图，以。为坐标原点，分别以OZ>,OE,OP所在的直线为X轴，y轴，z轴，

建立空间直角坐标系，则。(0,0,0),0(、/&,0,0),A(-#,0,0)，

P(0,0,36,C(而2&0),8(-76,2后0)，

因为点。是P£>的中点，所以。(当，0,之，)，

平面PAD的一个法向量为m=(0,1,0).

答案第14页，共20页

取用,2凤平)

显然正与配不共线，

所以CQ与平面尸4£)不垂直，所以A不正确；

定=(6,26,-3&),AQ=(孚,0,乎),AC=(2^,273,0).

设平面AQC的法向量:为八=(x,y,z),则

_/3任3拉n

nAQ=-----x-\-----z=0

22令x=l，则y=_&,z=_百，所以〃一\/§)，

n-AC=2瓜x+2\l^y=0

ruim

n■PC27612V2

设尸C与平面4QC所成角为。，则sin6=irj.uuB.=—产=二，所以cos8=----,所以B正确;

|n||pc|6x/633

三棱锥B-ACQ的体积为%TCO=%rsc=；£ABC.；°P=；xgx26x2#xgx3夜=6.

所以c不正确:

设四棱锥Q-ABCD外接球的球心为M(0,瓜a)，则MQ=MD,

所以［曰］+(@2+(叱¥［=(旬〉心门心

解得。=0,即M((),J§,0)为矩形ABCD对角线的交点，所以四棱锥Q-A3CQ外接球的半径为3,设四棱锥

Q-A8C。外接球的内接正四面体的棱长为x,将四面体拓展成正方体，其中正四面体棱为正方体面的对角线,

故正方体的校长为正方，

所以6?，得=24,所以正四面体的表面积为4X、2X?=24石，所以D

24

10.ABC

解：EF=OB=\-EFIIOB,四边形OFEB为平行四边形，所以OF//BE,

。尸(Z平面6C£，BEu平面BCE，所以。尸〃平面8CE，故A正确.

线段AB为圆0的直径，所以BF1FA-

矩形A8co所在平面和圆。所在平面垂直，平面A3CD「|平面A5EF=A3，ADu平面

ABCD，所以AD_L平面ABEF，BFu平面ABEF，所以AD_L3F

ADu平面A£)F，AFu平面AD尸，ADQAF^A,

所以BF、_L平面AOF，故B正确.

OF=OE=EF=\.△OFE是正三角形，所以EF=BE=AF=1，

DA/IBC，所以BC_UREA8EF，BC上BF，

BF=®CF=dCB?+BF2=百1=2,

DF=>]DA2+AF2=JiTT=72,

V14

AB=CD=2.ACDF是等腰三角形，ACOF的边。尸上的高Jc/2

亏’

DAIIBC-平面平面BC"ADFC

SAr„F=-x—xV2=—,AZ）uADF，8C（ZAOF，平面♦点

△CDF222

到平面ADF的距离为BF=5SADAF=；x1x1=；,VC_DM.=VA,CDF,

设点A到平面CDFE的距离为/?，

]XSBADFxFB=—xSMFDxh,—x—x百=—xxh•

所

所以〃=力，故c正确.

7

取OB的中点M，则MO〃A£），MO=~,所以MO，平面8尸石,

2

一：棱锥C—BEF外接球的体积为丫=弓%/=3%、（45]=*且不，故D错误,

3312J6

11.AB对于A,如图，以A为原点，AO,A8,AA1为坐标轴建立空间直角坐标系,

则4（0,0,0）,£（0,4,2）,4（0,0,4）,尸（4,2,0）,〃（4,0,4）,

.•.荏=（0,4,2）,即=（4,2,Y）,皿'=（4,0,4），

•.•荏•蒲=0x4+4x2+2x（T）=0..♦,AhAE,•.•9.4F=4X4+0X2+4X（T）=0,

二AFJ.A£>|,♦.•AEnAA=A，,AFJ.平面ARE,故A正确:

；C、B=2五,可知C|B//AQ.所以

对于B,如图，取用G中点G，连接RG,GE,则GE〃C|B且GE=

A,O1,G,E共面，则等腰梯形GE即为截面，可求得其面积为18,故B正确:

对于C,可知在正方体中，BC、“AD、,又BC\<z平面ARE,ARu平面ARE,所以BCJ/

答案第16页，共20页

平面因为P是8G上的动点，所有p到平面的距离为定值，故三棱锥P-AO|E的体积与尸点的位置无

关，故C错误;

对于D,设外接球心为0,过。作00'J_AE，垂足为O'，则以O'为圆心，O'A为半径的圆是过A£面积最小的截面圆,

迎故D错误.

5

根据图形的形成，知A,B,C三点在底面DEF上的射影分别是&DEF-:边中点M,N、P,如图，5c与/^MNP

全等且所在面平行，截而圆就是aA8c的外接圆与Z\M?VP的外接圆相同.

由题意△M7VQ的边长为1，其外接圆半径为r=X3xl=Y3,圆而积为S=;r/=J_,A错;

333

由上面讨论知AC与MP平行且相等，而MP与NF平行且相等，因此AC与NF平行且相

等,从而ACFN是平行四边形，CF//AN，所以NZM7V是异面直线40与CF所成的

角（或其补角）.由己知，A£>=2，DN=&，AN=CF=2,

AN2+AD2-ND24+4-35…,

cos4DAN=-------=—»B正确；

2ANAD2x2x28

由平面ADE与平面0EF垂直知AE在平而A£F内的射影是DE，所以NA£»为直线A0与平而。£户所成的角,

此角大小工，c正确.

3

4a4

由上面讨论知AB=BC=C4=1，设。是球心，球半径为R，由一4R=—乃得R=1，则0—ABC是正四而体,

33

n

棱长为1,设”是A44C的中心，则Oa_L平面A8C，又C”u平面ABC，所以OH_LCH，CH=—»

所以球离球托底面DEF的最小距离为73+—-1»D正确.

13.ACD

以8A,8C,881为x,y,z轴，建立如图所示空间直角坐标系，设A8=l，

其中A(1,0,1),01；,g,g),g(0,0,1),8(0,0,0),G(0,1,1),

因为丽=2月。，所以P（0",/l），

A.因为4P=A|POB|+9一;=0,

所以卒_1_函，所以4尸_1。与，故正确；

B.当2二：时，A^P=^—1,—,——^,AB=(—1,0,0),所以

1

Icos<^P,AB>\=,—=岖金

、"+土.142'

V99

所以直线AP与AB所成的角不是30°，故错误;

c.当/=g时，AP1111

t取平而4与a的一个法向量为“=((),0,1)，

-2

所以卜os<AA,〃>卜

=—,设直线A|P与平面ASG所成的角为夕

6

1+-+-V1

44

所以sin6=4,cose=1一,所以tanO=@，故正确;

5

D.当时，如图所示，p为BC中点，。为AC中点，连接OP.

1PQOP1

所以。2//^^，。/^二一4四，所以万元==彳,故正确;

2Q4A42

故选：ACD.

14.ABD

解：对于A选项，当6=90。时，四面体ABCQ的体积的最大值是V=』x立x22xj]=l，故A选项正确:

34

对于8选项，SACD=5e=6，

^ni-U△A/IBOC'

,:AB=AD=BC=CD，BD=BD，

:•△AB*ACBD.

:.SCRri=SARn=—AB-ADsin/.BAD=2sinNBAD<2，

所以，四面体A5CO的表面积的最大值是2x6+2x2=4+26,故5选项正确:

答案第18页，共20页

对于c选项，取AC中点尸，连接。尸，BF、

由题意，