第1课时圆周角和圆心角的关系

3.4圆周角和圆心角的关系第三章圆第1课时圆周角和圆心角的关系

问题1

什么叫圆心角？指出图中的圆心角.顶点在圆心，角的两边与圆相交的角叫圆心角，如∠BOC.A

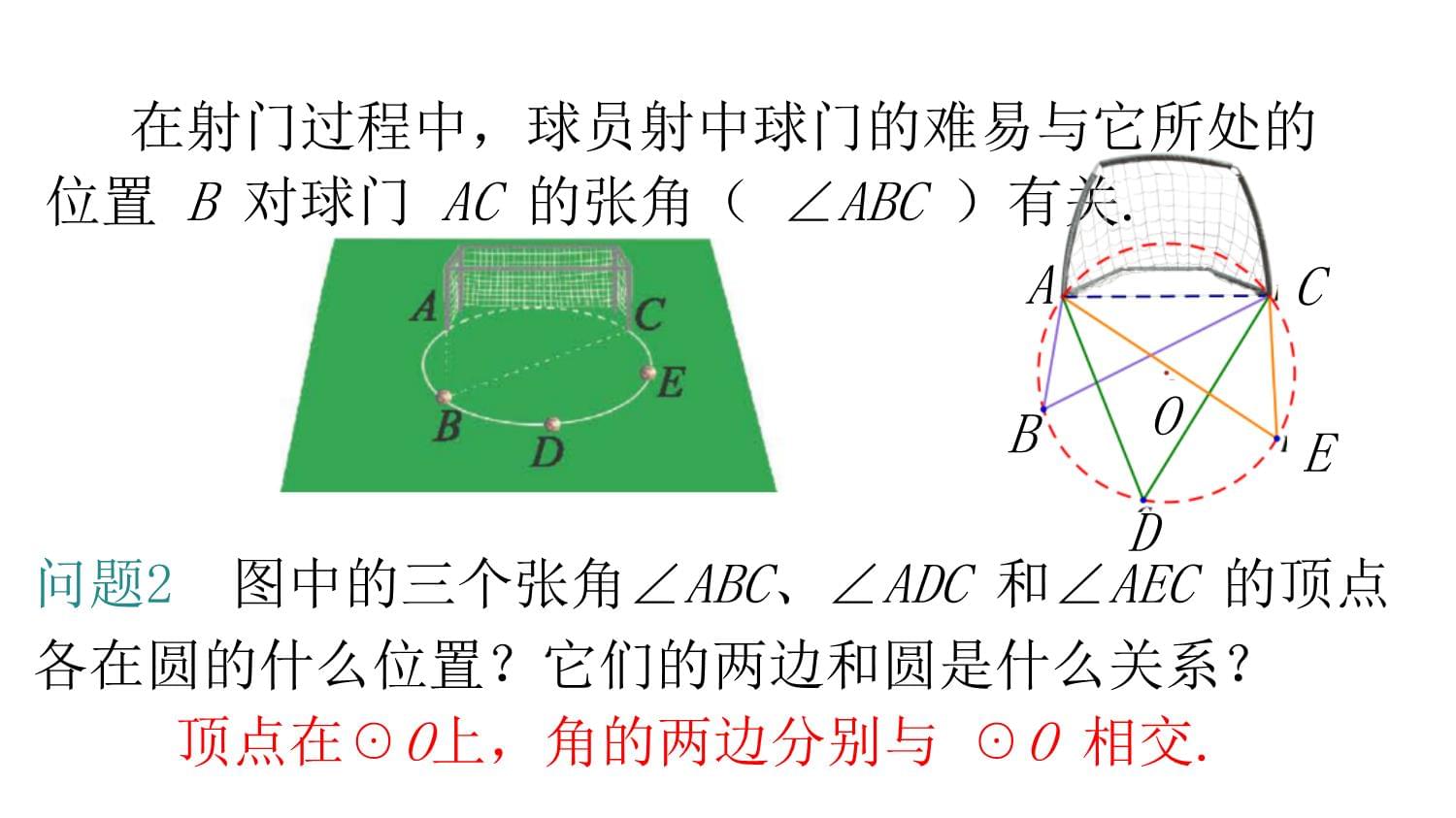
在射门过程中，球员射中球门的难易与它所处的位置

B对球门

AC的张角（∠ABC）有关.问题2图中的三个张角∠ABC、∠ADC和∠AEC的顶点各在圆的什么位置？它们的两边和圆是什么关系？

顶点在☉O上，角的两边分别与

☉O相交.ABDECO圆周角的定义1（两个条件必须同时具备，缺一不可）总结顶点在圆上，并且两边都与圆相交的角叫做圆周角.例如：∠ACB.ABOC·COAB·COB·COBAA·COAB·COB·COBAA1.下列各图中的∠BAC是否为圆周角？简述理由.顶点A不在圆上顶点

A不在圆上边

AC没有和圆相交√√√做一做2圆周角定理及其推论当球员在B，D，E

处射门时，他所处的位置对球门AC

分别形成三个张角∠ABC，∠ADC，∠AEC.这三个角的大小有什么关系？ABDECO如图，∠AOB=80°.（1）请你画出几个所对的圆周角，这几个圆周角有什么关系？与同伴进行交流.提示：思考圆周角和圆心角有几种不同的位置关系？做一做ABOCABOCABOCABO圆心

O

在∠C

的内部圆心

O

在∠C

的一边上圆心

O

在∠C

的外部(2)这些圆周角与圆心角∠AOB的大小有什么关系?猜想：

改变圆心角∠AOB的度数，上述结论还成立吗？议一议CABOCABOCABO圆心

O

在∠C

的内部圆心

O

在∠C

的一边上圆心

O

在∠C

的外部

证明：(1)圆心O

在∠C

的一条边上，如图.情况一：圆心

O在∠C的一边上

(特殊情形)已知：如图，∠C

是所对的圆周角，∠AOB

是所对的圆心角.求证：CABO∴∠AOB=2∠C，∵OA=OC，∴∠A=∠C.∵∠AOB

是△AOC

的外角，∴∠AOB=∠A+∠C.CABOCABO圆心

O

在∠C

的内部圆心

O

在∠C

的外部试一试：你能完成另两种情况的证明吗？合作探究已知：如图，∠C

是所对的圆周角，∠AOB

是所对的圆心角.求证：情况二：圆心

O在∠C的内部提示：能否转化为前一种已证明的情况?D过点

C作直径

CD.由已证可得：CABO情况三：圆心

O在∠C的外部提示：能否也转化为第一种已证明的情况?D过点

C作直径

CD.由已证可得:已知：如图，∠C

是所对的圆周角，∠AOB

是所对的圆心角.求证：CABO圆周角定理：一条弧所对的圆周角等于它所对的圆心角的一半.归纳总结CABOCABOCABO

在上面的射门游戏中，当球员在B，D，E

处射门时，所形成三个张角∠ABC，∠ADC，∠AEC

的大小有什么关系？你能用圆周角定理证明你的结论吗？●

O所以∠ABC

=∠ADC=∠AEC.根据圆周角定理，想一想归纳总结●

O推论：同弧所对的圆周角相等.1.

如图，点

A、B、C、D在☉O上，点

A与点

D在点

B、C所在直线的同侧，∠BAC=35°.(1)

∠BOC=

°，理由是

;(2)

∠BDC=

°，理由是

.7035同弧所对的圆周角相等一条弧所对的圆周角等于该弧所对的圆心角的一半练一练例1

如图，OA、OB、OC

都是

⊙O

的半径，∠AOB

=

50°，

∠BOC

=

70°.求∠ACB

和

∠BAC

度数.BCO.70°A∴∠ACB

=∠AOB

=

25°.同理∠BAC

=∠BOC

=

35°.

解：∵圆心角∠AOB与圆周角∠ACB

所对的弧为，典例精析圆心角类比圆周角圆周角定义圆周角定理圆周角定理的推论1圆周角的度数等于它所对弧上的圆心角度数的一半.同弧或等弧所对的圆周角相等.1.顶点在圆上；2.两边都与圆相交的角.1.判断（1）同一个圆中等弧所对的圆周角相等（）（2）相等的弦所对的圆周角也相等（）（3）同弦所对的圆周角相等（）√××2.已知

△ABC的三个顶点在

⊙O

上，∠BAC=50°，∠ABC=47°，

则

∠AOB=

．BACO166°3.如图，已知圆心角∠AOB=100°，则圆周角∠ADB=

.DAOCB50°4.如图，△ABC

的顶点

A、B、C都在

⊙O

上，∠C＝30°，AB＝2，则

⊙O

的半径是