西南交大版电路分析电子稿

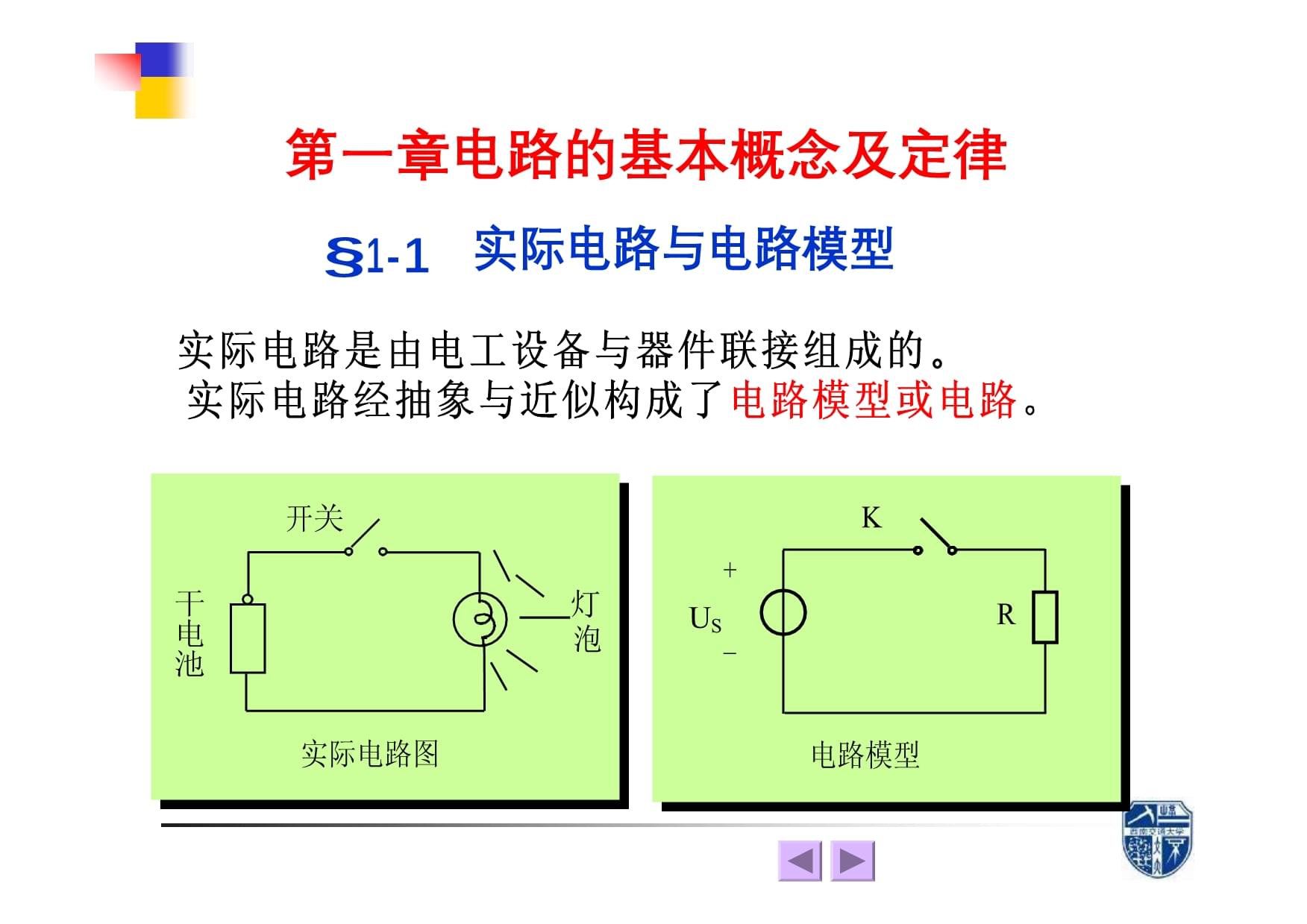
-实际电路是由电工设备与器件联接组成的实际电路经抽象与近似构成了电路模型或电路K开+- 泡R实际电路电路模-实际电路是由电工设备与器件联接组成的实际电路经抽象与近似构成了电路模型或电路K开+- 泡R实际电路电路模元件的分类：线性元件与非线性元件有源元件与无源元件二端元件与多端元件静态元件与动态元件集中参数元件与分布参数元件。元件的分类：线性元件与非线性元件有源元件与无源元件二端元件与多端元件静态元件与动态元件集中参数元件与分布参数元件。基本物理量与参考方向§1-基本物理量（基本变量）：iu，电量磁链，能基本物理量与参考方向§1-基本物理量（基本变量）：iu，电量磁链，能量W，功率电流的参考方向电流参考方向 元件 实际电流方向i>0电流参考方向i 元 实际电流方向i<i(t)电流的大小i(ti(t)电流的大小i(t)Iqt直电电流电流的单位：安培，简称安（A）千安（kA）、毫安（mA）、微安（μA）、纳安（nA）1kA1031A1061mA1031nA109电压的参考方向：又称参考极性电压又称电位差或电压降电压的大小:W WBWBWuAB电压的参考方向：又称参考极性电压又称电位差或电压降电压的大小:W WBWBWuAB（实际极性 u<（实际极性 u>电压单位：伏特（V）常用的有:千伏（kV）、毫伏（mV）、微伏（μV）关联参考方向：“+”极性流入、从否则为非关联参考方向“－”极性流出。i+u-电压单位：伏特（V）常用的有:千伏（kV）、毫伏（mV）、微伏（μV）关联参考方向：“+”极性流入、从否则为非关联参考方向“－”极性流出。i+u-关联参考方向i+u-非关联参考方向元件吸收的功率：关联参考方向p(t)u(元件吸收的功率：关联参考方向p(t)u(t)i(t)p(t)非关联参考方向P>0时，元件实际在吸收功率P<0时，元件吸收的是负功率，即元件实际释放功率功率的单位：瓦特简称瓦（W）、千瓦（kW）tWt0到t吸收的电能：to功率的单位：瓦特简称瓦（W）、千瓦（kW）tWt0到t吸收的电能：toWP(tt0直流情况下电能的单位：焦耳（J）1（J）=11kW·h（千瓦·小时电阻、电感和电容元件§1-一、电阻元件线性电阻在关联参考方向时，满足欧姆定律u(t)电阻、电感和电容元件§1-一、电阻元件线性电阻在关联参考方向时，满足欧姆定律u(t)i(t)Gu(t)R：线性电阻元件的电阻。G：线性电阻元件的电导 u 0-线性电阻电阻的单位：欧姆（Ω）电导的单位：西门子（S） +u 电阻的单位：欧姆（Ω）电导的单位：西门子（S） +u -非线性电阻R=0时，称其为“短路；R=时，称其为R=0时，称其为“短路；R=时，称其为“开路”或“断路”ui0R=的伏安特性ui0R=0的伏安特性电阻吸收的功率：关联参考方向条件下p(t)u(t)i(t)Ri2(t电阻吸收的功率：关联参考方向条件下p(t)u(t)i(t)Ri2(t)u2(t)Gu2R非关联参考方向时：p(t)u(t)i(t)Ri2(t)u2(t)Gu2Rt0到t内电阻消耗的能ttWpdtRi2t0t0二、电感元件1、电感：是一种储存磁场能量的元件。磁链:二、电感元件1、电感：是一种储存磁场能量的元件。磁链:N--线圈匝若－iL曲线是过原点的直线，则此电感为线性电感，且定义L 线性电感Ψi 0非线性电感L:电感量或电感值，为常数。单位：亨利简称亨（H）、毫亨（mH）2、电感上电压与电流的关系：uL与iL取关联参考方向时u(t)dLiL:电感量或电感值，为常数。单位：亨利简称亨（H）、毫亨（mH）2、电感上电压与电流的关系：uL与iL取关联参考方向时u(t)dLiLdiLL取非关联参考方向时 (t)LdiL+ -直流电路中，电感两端电压为零，电感相当于短路；当电流变化剧烈时，电感两端出现高电压。ud1LLtu00tuiLLLLL(0)tuLL直流电路中，电感两端电压为零，电感相当于短路；当电流变化剧烈时，电感两端出现高电压。ud1LLtu00tuiLLLLL(0)tuLLL0iL(0):初始值。电感是记忆元件3、功率和能量关联参考方向下，电感吸收的功率Lpii Lpp吸收能量释放能量0到t吸收的能量:1212ttWpddtLi(t)pp吸收能量释放能量0到t吸收的能量:1212ttWpddtLi(t)22LiLLL0t时刻具有的能量:W1Li2L2三、电容元1、电容：是一种储存电场能量的元件。C线三、电容元1、电容：是一种储存电场能量的元件。C线性电容器的电容单位：法拉简称法（F）1F106F109nF1012 -线性电 非线性电2、电容上电压与电流的关系id11t0tid iccccCCC01t(0)idccC0uc—初始值i2、电容上电压与电流的关系id11t0tid iccccCCC01t(0)idccC0uc—初始值i(t)c非关联参考方向时：c直流时，电容相当于开路；当电压变化时，电容流才有i(t)dq Cduc(关联 3、功率和能量关联参考方向下，电容吸收的功率:ppC吸收能量释放能量puu c0到t吸收的能量:1212tpd 3、功率和能量关联参考方向下，电容吸收的功率:ppC吸收能量释放能量puu c0到t吸收的能量:1212tpd tWdtCu(t)22Cuccc00t时刻具有的能量:W122Cu(t)c独立电§1-独立电源（又称激励源）：电压源和电流源u(t)us独立电§1-独立电源（又称激励源）：电压源和电流源u(t)us流过的电流取决于外电路一、电压源时，相当于“短路”当++ --电路符号ui0t时刻的伏安特性直流情况:电压源发出的功率：（非关联p(t)us(t)i(直流情况:电压源发出的功率：（非关联p(t)us(t)i(t)i + -电路符ui0伏安特实际电压源：uusu R实际电压源：uusu Ri i+-+u-二、电流电流源的特性:i(t)is二、电流电流源的特性:i(t)is其端电压取决于外部电路i + _电路符号ui0伏安特性当时，相当于“开路”电流源发出的功率（非关联当时，相当于“开路”电流源发出的功率（非关联p(t)u(t)isp(t)u(t)is电流源吸收的功率ui0is=0的伏安特性实际电流源：Risiu s端口的伏实际电流源：Risiu s端口的伏安特性i -电路模型受控电源§1-受控电源是多端元件，有四种类型。电流控制电流源（CCCS）+ g-电压控制电流源（VCCS） 受控电源§1-受控电源是多端元件，有四种类型。电流控制电流源（CCCS）+ g-电压控制电流源（VCCS） 电压控制电压源（VCVS） r1电流控制电压源（CCVS）基尔霍夫定§1-基尔霍夫电流定律简称基尔霍夫电压定律简称基尔霍夫定§1-基尔霍夫电流定律简称基尔霍夫电压定律简称一、名词介支在电路中，一般可以把一个二端元件当成一条支路。但为了方便起见，通常把流过同一电流的分支称为一条支路。a支路：acb、adb、abd+c+__b结一般认为支路间的联接点即为结点。为简便起见，今后则定义三条和三条以上的支路联接点为结点。如a、b结点。a支路：acb、adb、abd+c+__b结一般认为支路间的联接点即为结点。为简便起见，今后则定义三条和三条以上的支路联接点为结点。如a、b结点。回电路中的任何一条闭合路径称为回路。如acbda、acbaadbaad+c+__b回电路中的任何一条闭合路径称为回路。如acbda、acbaadbaad+c+__ba网在回路内部如果不含任何支路时，则称该回路为网孔。d+c+__如acbda、adbab二、基尔霍夫电流定律（KCL）：在集中参数电路中，对于任意一个结点来说，任何时刻流出该结点的各支路电流的代数和等于零。即nik a网在回路内部如果不含任何支路时，则称该回路为网孔。d+c+__如acbda、adbab二、基尔霍夫电流定律（KCL）：在集中参数电路中，对于任意一个结点来说，任何时刻流出该结点的各支路电流的代数和等于零。即nik k假设流出该结点的电流为正，那么流入即为负，于是有:i1i2i3假设流出该结点的电流为正，那么流入即为负，于是有:i1i2i3或iii1234即i1KCL也可描述为：在集中参数电路中，对于任意一个出的电流之和。引申到一个闭合面（又称高斯面、广义结点）：合面的电流。i1i2 ①iii引申到一个闭合面（又称高斯面、广义结点）：合面的电流。i1i2 ①iii证'1133i2i2'i1 i3'i2三等式相②③i2i1i22siniii,例1：已知123bacd i2i3解i12sint3e2siniii,例1：已知123bacd i2i3解i12sint3e 例2：已知i22A1A,6,例2：已知i22A1A,6,i i3ii50解 i2 2165A三、基尔霍夫电压定律（KVL）对于集中参数电路来说，在任何时刻，沿任一闭合回路绕行一周,各支路电压的代数和等于零。即u1＋＋－ab＋ue假设电压的参考方向与绕行的方向一致时取“”2－－ucd4＋u3＋取“－”u三、基尔霍夫电压定律（KVL）对于集中参数电路来说，在任何时刻，沿任一闭合回路绕行一周,各支路电压的代数和等于零。即u1＋＋－ab＋ue假设电压的参考方向与绕行的方向一致时取“”2－－ucd4＋u3＋取“－”u1u2nuk ku1＋＋－auub1u23＋－eu4u5－u4cdu＋＋u3u1＋＋－auub1u23＋－eu4u5－u4cdu＋＋u3ad即：两点间的电压与路径无关。注意：（1）KCL，KVL只用在集中参数电路中（布参数不适用）；（2）KCLKVL与元件的性质无关。所以线性、非线性电路均适用。例3：支路电流如图所标，列出该回路的KVL方程。解：根据KVL可列出：iba1+-RRius 1+-R3i3R4i4 usR1例3：支路电流如图所标，列出该回路的KVL方程。解：根据KVL可列出：iba1+-RRius 1+-R3i3R4i4 usR1i1R2i2即dcR3i3R4usus电阻上电压的代数和等于电动势的代数和。Rk即例4：求支路电流i1i2i3。已知us1us2V,us35V,KCLi例4：求支路电流i1i2i3。已知us1us2V,us35V,KCLii-123u+KVL方程回路+u-uRu2s回路us2R2i2us3i13A,i21A,2联立求解得 u-§2-电阻的串联、并一、电阻的串ii＋＋＋un－＋u1＋nuRuk－－ nuu1§2-电阻的串联、并一、电阻的串ii＋＋＋un－＋u1＋nuRuk－－ nuu1 uk所R:等效电阻输入电kuR1iR2iRni(R1R2Rn)i Ri 分压:kkR电路吸收的总功率pui(u1u2unnk二、电阻的并ii＋ Ri 分压:kkR电路吸收的总功率pui(u1u2unnk二、电阻的并ii＋＋nuｕGk－－nii1i2ininii1i2inikki(G1G2Gn)unGkGG1G2kG：等效电导、输入电导 Gui分流kkGpui(i1i2inn电路吸收的总功率 p1 k电路如图。求：例2－1cabd解：（1）求解aaaΩΩΩΩΩbbb电路如图。求：例2－1cabd解：（1）求解aaaΩΩΩΩΩbbbc(2)求dccddc(2)求dccdd求惠斯通电桥的平衡条件例a解：电桥平衡时ig 0, i3cduab另GR4所求惠斯通电桥的平衡条件例a解：电桥平衡时ig 0, i3cduab另GR4所bRR－＋即uad1 R4即R故电桥平衡的条件：R即 RR34-星形（Ｙ）一、电阻的三角形（Δ）与星形（Ｙ）联a三角形（Δ）联接如R1R2-星形（Ｙ）一、电阻的三角形（Δ）与星形（Ｙ）联a三角形（Δ）联接如R1R2R5星形（Ｙ）联接:如R1R5R3二、Δ联接与Ｙ联接的等效变R3R4bＹ→Δ已知R1、R2、R3求R12、R23、uab a根据KCLi1i12 iR i2RR i已知R1、R2、R3求R12、R23、uab a根据KCLi1i12 iR i2RR i cb3RRaR1i1R2iR2 uab根据KVLR1oR3i3 ubccbi1i2 另根据KCLi3RR RRRi3RR RRR RRRRR i2RR RRR RRRRR i1R RRR R RRR R1R2R2R3R3RR2 同2RR1R2R2R3R3RR2 同2RRR R23 R R31 R1R2R2R3R3 1 R1R2R2R3R3 3且R时。例2－3：求RabaaRRR32bb 3 1.5且R时。例2－3：求RabaaRRR32bb 3 1.52 1解R135235 1 2 0.633541.525.50.89R2另解Ｙ→Δ变换1a231R11R1a12233 2 0.633541.525.50.89R2另解Ｙ→Δ变换1a231R11R1a1223310.63RaR23R1R1223323 b2R245.5R5.5 b电路如图，各电阻的阻值均为1Ω。试例2－4求ab间的等效电阻。aaa①③③③②②②bbbaa③③②②bb 2 电路如图，各电阻的阻值均为1Ω。试例2－4求ab间的等效电阻。aaa①③③③②②②bbbaa③③②②bb 2 图示电路为一个无限链形网络，每个环例2－5节由R1与R2组成，求输入电阻RababbR2,2RRR1 2R24RR R2图示电路为一个无限链形网络，每个环例2－5节由R1与R2组成，求输入电阻RababbR2,2RRR1 2R24RR R2R1 4R12R由于>0,所以ab2电源的串联、并§2-一、电压源的串联与并电压源的串联:i+–+––+i＋＋+－uu－电源的串联、并§2-一、电压源的串联与并电压源的串联:i+–+––+i＋＋+－uu－ －uu1u2u3根据KVL电压源的并联:大小相等、方向相同 二、电流源的并联与串电流源的并联：ii++uu__i根据KCL电流源的串联:大小相等、方向相同二、电流源的并联与串电流源的并联：ii++uu__i根据KCL电流源的串联:大小相等、方向相同对外电路而言:aaaa＋＋－bbbbaaaa＋isus＋－－bbbb＋－－对外电路而言:aaaa＋＋－bbbbaaaa＋isus＋－－bbbb＋－－例2-求电阻和电流源上的电压。－＋＋+＋uu12－－u1－51010u11050u2解例2-求电阻和电流源上的电压。－＋＋+＋uu12－－u1－51010u11050u2解- ii+u-+u-Rii +s-iu1uR对图即siRR1ii对图iusRi故 u,R'- ii+u-+u-Rii +s-iu1uR对图即siRR1ii对图iusRi故 u,R' aa +_isRibb将图示电路等效为电压源串电阻的形式。例2-iiaa_+b b检查方法：等效变换前后两电路的开路电压应相等等效变换前后两电路的短路电流应相等。注意:理想电压源和理想电流源不能进行aa +_isRibb将图示电路等效为电压源串电阻的形式。例2-iiaa_+b b检查方法：等效变换前后两电路的开路电压应相等等效变换前后两电路的短路电流应相等。注意:理想电压源和理想电流源不能进行等效变换us。用电源等效变换法求流过负载的电流例2-＋I＋－I－R2IIR2I＋－I 4 612。用电源等效变换法求流过负载的电流例2-＋I＋－I－R2IIR2I＋－I 4 612§3-支路电流待求变量：支路电流根据KCL建立独立的电流方程§3-支路电流待求变量：支路电流根据KCL建立独立的电流方程根据KVL建立独立的电压方程用支路电流法求解图示电路。例3－1BI1ACR5R4R3D-+Us解：各支路电流如图所设，变量有6用支路电流法求解图示电路。例3－1BI1ACR5R4R3D-+Us解：各支路电流如图所设，变量有6BRR21RA5CII6D4-+RUs6I1I4IKCL方程结点结点BBRR21RA5CII6D4-+RUs6I1I4IKCL方程结点结点B结点CI1I2 I2I3I BKVL方程回路R1I1R5I回路I1R1RA5C1R4I 2I43IBKVL方程回路R1I1R5I回路I1R1RA5C1R4I 2I43II36D4R2I2R3I3R5I 回路-+RUs6R4I4R3I3UsR6I联立求解得支路电流确保回路方程独立的充分条件：每一个回路必须至少含有一条其它回路所没有的支路。例3－2用支路电流法求u1和u2。已知3,us11V,us确保回路方程独立的充分条件：每一个回路必须至少含有一条其它回路所没有的支路。例3－2用支路电流法求u1和u2。已知3,us11V,us＋us＋＋＋u2u－－－－解＋us－i1 ＋＋ us1R1i1usR2解＋us－i1 ＋＋ us1R1i1usR2 31－R R2－1s i1解i2u11.143回原电路求 R3i3usR2i2§2结点电压§2结点电压法（结点电位法变量：结点电压方法：对独立结点（通常选除参考点以外的结点建立关于结点电压的KCL方程结点电压：任选电路的某一结点作为参考点，并假设该结点的电位为零（通常用接地符号或0示），那么其它结点到该结点的电压就是结点电压，又称结点电位。usR＋－7①②③＋－R5is（或0）结点电压：u1、u2、usR＋－7①②③＋－R5is（或0）结点电压：u1、u2、几点说明：电路中所有的量均可由结点电压表示。usR＋－7①②③＋－R5is（或0）u2u1us1usu3usii17RRR177几点说明：电路中所有的量均可由结点电压表示。usR＋－7①②③＋－R5is（或0）u2u1us1usu3usii17RRR177 结点电压自动满足usR＋－7①②③＋－R5i21s（或0）u1u2而 u1u2回路u1u1u2u2 结点电压自动满足usR＋－7①②③＋－R5i21s（或0）u1u2而 u1u2回路u1u1u2u2u3u3回路如果一个电路有n个结点、b条支路变量的个数：（n－1如果一个电路有n个结点、b条支路变量的个数：（n－1）KCL方程的数目：（n－1）⑶结点电压法比支路电流法少了b-(n-1)个变量。一、电路中没有不串联电阻的电压源usR＋－7②①③＋－is（或0）结点电压u1、u2、u3如图所设。假设流出结点的电流为正，流入为负。一、电路中没有不串联电阻的电压源usR＋－7②①③＋－is（或0）结点电压u1、u2、u3如图所设。假设流出结点的电流为正，流入为负。usR＋－7②①③＋－is（或0）1(u)11u)1uuu)111213sRRR3127111u) )21223RRR3451u)1usR＋－7②①③＋－is（或0）1(u)11u)1uuu)111213sRRR3127111u) )21223RRR3451u)11u)32331ssRRR567usR＋－7②①③＋－is（或0）11111us(1 u123RRR1R1RRRR12373717111u123R1RRRR33455(11111uuu123ssRRRRRR755677usR＋－7②①③＋－is（或0）11111us(1 u123RRR1R1RRRR12373717111u123R1RRRR33455(11111uuu123ssRRRRRR755677usR＋－7②①③＋－is（或0）1111是与结点①相联的各支路电导的总和，称为结点①的自电导，且为正。RRRR12371是结点①与结点②之间usR＋－7②①③＋－is（或0）1111是与结点①相联的各支路电导的总和，称为结点①的自电导，且为正。RRRR12371是结点①与结点②之间各支路电导之和并取负称其为结点①与②的互电导，为负R31是结点①与结点③之间各支路电导之和，并取负R7流入结点①的电流源之和，且入为正，流流入结点①的电流源之和，且入为正，流出为负RR17简写为G11u1G23u3G33u3G22u2G32u2列出图示电例路的结点电压方程。解：选结点5为参考结点，结点电压分别为u、u、u、1234(G1 G3)u1G2 列出图示电例路的结点电压方程。解：选结点5为参考结点，结点电压分别为u、u、u、1234(G1 G3)u1G2 G3u4G1us1is9G1u1(G1 G6)u2 G4u3is6 G2u1G4u2 G5G7)u3G5u4G7us7G3u1G5u3 (G3G5G8)u41 2 us7－ 5例电路如图。用结点电压法求电流I2和以及各电源发出的功率。a＋－＋－＋解：结点电压为a0.4U11311 －260.42II2320.230.2UaUa所UIIa2323例电路如图。用结点电压法求电流I2和以及各电源发出的功率。a＋－＋－＋解：结点电压为a0.4U11311 －260.42II2320.230.2UaUa所UIIa23232I3I3求电流源上的电压U1及功率0.4U1U1Ua10.4用例3－512点电压法求图示电路的结点电压u1和u23i解：(11)u 4121010(11 uiu2 3i1210用例3－512点电压法求图示电路的结点电压u1和u23i解：(11)u 4121010(11 uiu2 3i1210联立求解得1055u1u2两个实际电压源并联向三个负载供电。其例3－6中R1、R2分别是两个电源的内阻，R3、R4、R5为负载，求负载两端的电压。－＋－＋us(11111 us1)u解：结点电压两个实际电压源并联向三个负载供电。其例3－6中R1、R2分别是两个电源的内阻，R3、R4、R5为负载，求负载两端的电压。－＋－＋us(11111 us1)u解：结点电压(G1G2G3 G5)uG1us1G2us即G1us1G2usu所G1G2G3G4二电路中有不串联电阻的电压源例电路如图所示。求结点①与结点②之。间的电压u12②③①+--+二电路中有不串联电阻的电压源例电路如图所示。求结点①与结点②之。间的电压u12②③①+--+解法1：假设流过22V电压源的电流为i②③①+--+u3)3(u1u21)8①②③联立求解得u1u2u1)1i解法1：假设流过22V电压源的电流为i②③①+--+u3)3(u1u21)8①②③联立求解得u1u2u1)1i3(u2124(u3u1)i5u3u3 u2 u1u2所解法2：将22V电压源包围在封闭面内②③①+--+4(u1u3)u21)8结点①广义结点辅助方程4(u3u1) 解法2：将22V电压源包围在封闭面内②③①+--+4(u1u3)u21)8结点①广义结点辅助方程4(u3u1) u11)15u325u3u1u2联立求解得u1解法3：假如参考结点可以任意选择③①+--+②4u13(u1u31)881(u2u3)5u2解法3：假如参考结点可以任意选择③①+--+②4u13(u1u31)881(u2u3)5u225u3结点①结点②结点③联立求解得u2u1u1u3例用结点电压法求I解：U1、U2U如图。3U 1U12(U1例用结点电压法求I解：U1、U2U如图。3U 1U12(U1U2)3(U3U2)5结点②:广义结点:辅助方程:联立求解得所以U1U3I12(U1U2U U U1 I3(U2U3) - +3变量——网孔电流。方法——沿网孔建立独立的KVL方程。网孔电流法只适合于平面电路。平面电路——可以画在平面上，而又不出现支路交叉的电路。+--+3变量——网孔电流。方法——沿网孔建立独立的KVL方程。网孔电流法只适合于平面电路。平面电路——可以画在平面上，而又不出现支路交叉的电路。+--+网孔电流——环流于网孔各支路的电流。+-网孔电流自动满足KCL方程。立体电网孔电流为一组独立的求解变量。如果电路有n个节点、b条支路，则网孔电流的数目为b－(n－1)个，比支路电流法少n－1个变量一、电路中没有不并联电阻的电流源网孔电流——环流于网孔各支路的电流。+-网孔电流自动满足KCL方程。立体电网孔电流为一组独立的求解变量。如果电路有n个节点、b条支路，则网孔电流的数目为b－(n－1)个，比支路电流法少n－1个变量一、电路中没有不并联电阻的电流源(i1i3＋网孔电流为i、i和123R2－假设电压降方向与网孔电流的流向一致时取正、反之取负。i1＋u－i3＋s—i2(i2i3us1(i1i3＋网孔电流为i、i和123R2－假设电压降方向与网孔电流的流向一致时取正、反之取负。i1＋u－i3＋s—i2(i2i3us1R2i3)R3(i1i2)us3i1网孔i2i3网孔us3 R3 i1)R5 i3)(R4 R6R5(i3i2)R2(i3i1)us2(R1 R3)i1 R2i3(R1 R3)i1 R2i3us1整理得RiRR R3345 5R2i1 (R2 R5)i3usR3R1i1网孔的自电阻，为正是i1与i2网孔的互电阻。在共用的支路上，i1与i2方向相同取“+”，反之取“–”。是i1与i3网孔的互电阻。在共用的支路上，当i1与i3方向相同时取“+”，反之取“–”。us1us3是i1网孔内电压源的代数和。电压源压降的方向与为关联参考方向时取“–”，反之取“+”。R11i1R11i1u22简写成当电路中没有受控源时：－＋例用网孔i＋法求流过6Ω阻的电流i－6ii21解：网孔电流i1i2和i3如图所设4(862)i16i2i1网孔i2网孔－＋例用网孔i＋法求流过6Ω阻的电流i－6ii21解：网孔电流i1i2和i3如图所设4(862)i16i2i1网孔i2网孔i3网孔解得i1(6(24)i3ii22Ai2i3例电路如图。求网孔电流i1和i2i＋＋us－－解i解1s2i1例电路如图。求网孔电流i1和i2i＋＋us－－解i解1s2i1(2ii1i2s辅助方程二、电路中有不并联电阻的电流源试求电路中的网孔电流。例2＋－i27二、电路中有不并联电阻的电流源试求电路中的网孔电流。例2＋－i272＋解法1：假设电流源上的电压为－＋u－71i3i1网孔i2网孔2＋解法1：假设电流源上的电压为－＋u－71i3i1网孔i2网孔i3网孔辅助方程联立求解3(i2i1)1i2u1(i3i1)u7i2i3i12.5A,i22A,i392解法2：网孔电流i1、i2和i3仍如原图所设＋－7(123)i13i212解法2：网孔电流i1、i2和i3仍如原图所设＋－7(123)i13i21i1网孔超网孔或广义网孔的KVL方程为:1(i3i1)3(i2i1)1i27i2i3i12.5A,i22A,i39辅助方程：联立求解得：4例试求电i1路的网孔电流。＋－解：网孔电流i＋1i2和i3如图所设。i2网孔2－4i23i1超网孔即辅助方程：3(i14例试求电i1路的网孔电流。＋－解：网孔电流i＋1i2和i3如图所设。i2网孔2－4i23i1超网孔即辅助方程：3(i1i2)7i14i2i1 1i2)3(i2i1i31.17i1i2联立求解得：3一、拓扑图拓朴图是由结点与线段组成的图形，简称为图。+-1、有向图（定向图）：标有电流参考方向的图称为有向图，否则为无向图。3一、拓扑图拓朴图是由结点与线段组成的图形，简称为图。+-1、有向图（定向图）：标有电流参考方向的图称为有向图，否则为无向图。2、子图：如果图G1的每个结点和每条支路都是图G的，则称图G1是图G的子图。12②②②12①③③①③①4443355④④④22②②②③③①①③44533④④④2、子图：如果图G1的每个结点和每条支路都是图G的，则称图G1是图G的子图。12②②②12①③③①③①4443355④④④22②②②③③①①③44533④④④3、路径：从图G的某个结点沿不同支路及结点到达另一结点，那么所经过的支路序列称为路径4、连通图与非连通图：图3、路径：从图G的某个结点沿不同支路及结点到达另一结点，那么所经过的支路序列称为路径4、连通图与非连通图：图G中的任意两个结点之间至少存在一条路径时，则称图G为连通图，否则为非连通图。5、孤立结点：没有任何支路与之连接的结点。接的结点同时移去；但是说移去一个结点，则意味着与该结点相连的支路也移去了。二、树1、树：设图G是一个连通图，图T是图G的一个子图，当图T同时满足下列三个条件时，则称图T是图G的一棵树。（1）（2）（3）是一个连通的子图。包含图G的全部结点。不包含回路。树：连接全部结点所需的最少支路的集合。2（1）（2）（3）是一个连通的子图。包含图G的全部结点。不包含回路。树：连接全部结点所需的最少支路的集合。2、树支：组成树的支路称为树支。3、连支：除去树支后所剩支路即为连支。三、回路与基本回路1、回路：一个闭合的路径。2、基本回路：仅由一条连支与多条树支构成的回路。基本回路的方向与连支的方向一致。125876341258763411225588776633441122558877663344四、割集与基本割集1、割集：是支路的集合，它必须满足两个条件：移去该集合中的所有支路，则图被分为两部分。当少移去该集合中的任何一条支路，则图仍是连通的。注：移支路时，与其相连的结点并不移去1112四、割集与基本割集1、割集：是支路的集合，它必须满足两个条件：移去该集合中的所有支路，则图被分为两部分。当少移去该集合中的任何一条支路，则图仍是连通的。注：移支路时，与其相连的结点并不移去111222555333444666111222555343344666不是图G的集2、作高斯面确定割集：在图G上作一个高斯面（闭合面），使其包围G111222555343344666不是图G的集2、作高斯面确定割集：在图G上作一个高斯面（闭合面），使其包围G的某些结点，而每条支路只能被闭合面切割一次，去掉与闭合面相切割的支路，图G将被分为两部分，那么这组支路即为图G的一个割集。221155344366221155344366C4为非基本割集割集C1、C2、3、基本割集：先选一棵树，如选支路1、5、3为树枝。基本割集又称单树支割集支，其余均为连支。212155343466基本割集数：设有n212155343466基本割集数：设有n个结点、b条支路树支数＝n-基本割集数＝n-§特点：平面§特点：平面电路、立体电路均适用。变量：基本回路电流方向：与连支电流的方向一致。方法：沿基本回路建立KVL方程。方程数：设网络的图有n个结点，b条支路b-（n-方程数＝连支数＝选一个合适的树：把电压源支路选为树支；把受控源的电压控制量选为树支；把电流源选取为连支；把受控源的电流控制量选为连支。选一个合适的树：把电压源支路选为树支；把受控源的电压控制量选为树支；把电流源选取为连支；把受控源的电流控制量选为连支。例3-13：用回路法求解电路解：选树如图，回路电流如图2i132(i1i2)2例3-13：用回路法求解电路解：选树如图，回路电流如图2i132(i1i2)266i232(i1i2)224i36 -i3i1i2i3i1i2解如按右图选树：所以网孔电流法是回路法的一个特例。例3-14：试用回路法求i1+1-例3-14：试用回路法求i1+1-解：选树如图，回路电流为i1、i24A、+11V-(31025)i15i2(1025)4解：选树如图，回路电流为i1、i24A、+11V-(31025)i15i2(1025)4(25)3i15i1(125)i2545 41i15i2解i120i12例3-15：要使i＝0，确定gm的值。+u-i++--41i15i2解i120i12例3-15：要使i＝0，确定gm的值。+u-i++--解：选树如图i回路11i11igmu1)1igmu)即+3iumu辅助方程：-iu1(i1解：选树如图i回路11i11igmu1)1igmu)即+3iumu辅助方程：-iu1(i1im++ 解im3gm-- 所§变量：树支电压。方法：根据基本割集建立KCL§变量：树支电压。方法：根据基本割集建立KCL方程。方程数：有n－1个树支电压，方程数＝n－1选一个合适的树：将电压源及电压控制量选为树支，电流源及电流控制量选为连支。例C3563C2141+-Ru5s步骤：（1）选一个“合例C3563C2141+-Ru5s步骤：（1）选一个“合适”的树，并给各支路定向画出基本割集及其参考方向。写基本割集的KCL方程u3u2u1usu1RRR153u3CC21Ru Ri2123u3u2u1usu1RRR153u3CC21Ru Ri21232134sRRR431u3u2+-Ru5su1isRR12（4）联立求解，得树支电压u1、u2、u35C163241结点电压法是割集法的特例。5C163241结点电压法是割集法的特例。例2：重做例3－7所示电路。C3+--+解：选树支电压：u1、u2和。u3＝22V已知，可不建立u3的割集方程。例2：重做例3－7所示电路。C3+--+解：选树支电压：u1、u2和。u3＝22V已知，可不建立u3的割集方程。uC33-1V-+22)33u1881uC33-1V-+22)33u1881u15(22u2)25u1u2解得例3：已知：G1G22S,G33SG55S,1V3V试用割集分析法例3：已知：G1G22S,G33SG55S,1V3V试用割集分析法i1及电压源us1发出的功率。G1+-G2-++u-i5+-解：选树如图，树支电压u1、u4、u6 us6u4us4∵∴可不建立关于u4和u6的基本割集方程。+-G2-++Gu解：选树如图，树支电压u1、u4、u6 us6u4us4∵∴可不建立关于u4和u6的基本割集方程。+-G2-++Guu54-i5+-G1+-G2-++Gu5-i5+-G1(u1us1)G2us6)G5(usG1+-G2-++Gu5-i5+-G1(u1us1)G2us6)G5(usus6)is3 8u124u1即得i1G1(u1us1)(31)4∴us1i1第四线性电路的基本定理叠加原§4-叠加原理只适合于线性电路。利用下图讨论。+-u+-(R1R2R2第四线性电路的基本定理叠加原§4-叠加原理只适合于线性电路。利用下图讨论。+-u+-(R1R2R2i1us1usR3us2 iu1R RR R2uissR RR iu1R RR R2uissR RRRRR 当us1单独作用时，令us2＝0，is＝0 i'u1R RR 当us2单独作用时，令us1＝0，is＝0i''u1sR RR 当is单独作用时，令us1＝0，us2＝0R2i'''i1s当is单独作用时，令us1＝0，us2＝0R2i'''i1sR RR i1i1'i1''i1'''所电源为零：电压源为零：用短路线代替电压源。电流源为零：用开路代替电流源。图示叠加原理：如求电流ii+-i+uuuRR+R-233-i-iu＋＋+i+-i+uuuRR+R-233-i-iu＋＋+ii'i''i'''那注意：电流、电压可以叠加，但功率不能用叠加求得。叠加时注意电压、电流的参考方向。受控源不能单独作用，受控源应保留在电路里。线性系统有两个基本性质：叠加性、齐次性。例4-1：求U（梯形电路12++2222U--ii'i''i'''那注意：电流、电压可以叠加，但功率不能用叠加求得。叠加时注意电压、电流的参考方向。受控源不能单独作用，受控源应保留在电路里。线性系统有两个基本性质：叠加性、齐次性。例4-1：求U（梯形电路12++2222U--UU解：利用齐次性UsUs设U那1(31)353V结点2：222432115UU解：利用齐次性UsUs设U那1(31)353V结点2：222432115)u14V4结点1：12221)uU1 s18U84UU所sUs例4-2：用叠加原理求U-+I++U-5A-10I10I-+-+I+++IUU5A＋---例4-2：用叠加原理求U-+I++U-5A-10I10I-+-+I+++IUU5A＋---10I解：10V作用时：IU'10I'4I'-++I+U--5A作用时：I''10I解：10V作用时：IU'10I'4I'-++I+U--5A作用时：I'' 52A10I-+6U''10I''6I''+IU5AUU'U''所-替代定§4-替代定理：电路中的任何一条支路，如其端压uk或电流ik已知，那么这条支路可以用电压为uk的电压源或电流为ik的电流源替代，替代后不会影响电路各支路的电流和电压。图示替代定理：++经计算知I2替代定§4-替代定理：电路中的任何一条支路，如其端压uk或电流ik已知，那么这条支路可以用电压为uk的电压源或电流为ik的电流源替代，替代后不会影响电路各支路的电流和电压。图示替代定理：++经计算知I2U+U---右侧支路用电流源替代I3++U--右侧支路用+++电压源替代U---右侧支路用电流源替代I3++U--右侧支路用+++电压源替代U---例4－3：求各支路电流。+- 10解10151510I3I例4－3：求各支路电流。+- 10解10151510I3I 64（1）把R4用电流源替代结点法：(11)U110+55U-得1106010I156RRI312+I-（1）把R4用电流源替代结点法：(11)U110+55U-得1106010I156RRI312+I- 43（2）把R2用电压源替代+解得：-1106010AI15 6043RR31+I I16+（2）把R2用电压源替代+解得：-1106010AI15 6043RR31+I I16+R4--（3）R2用电流源、R4用电压源替代结点法：+11 )U6-5得555U110 10ARI12+5+ 6（3）R2用电流源、R4用电压源替代结点法：+11 )U6-5得555U110 10ARI12+5+ 62-60- 45戴维南定理与诺顿定理§4-二端网络：对外具有两个端钮的网络，又称单口网络、一端口网络。负载RL分别取2Ω和4Ω时，求流过该负载的电流。a20V-+I+I--+bb戴维南定理与诺顿定理§4-二端网络：对外具有两个端钮的网络，又称单口网络、一端口网络。负载RL分别取2Ω和4Ω时，求流过该负载的电流。a20V-+I+I--+bb-20Va+26V-IIbbI 5A3.22R＝2Ω时，LIR＝4Ω时，L3.2-20Va+26V-IIbbI 5A3.22R＝2Ω时，LIR＝4Ω时，L3.2戴维南定理：任何一个含有独立电源的线电阻二端网络，对外电路来说，总可以等效为一个电压源串电阻的支路，该电压源等于原二端网络的开路电压uoc，电阻Ro等于该网络中独立电源置零后在端口处的等效电阻。a戴维南定理：任何一个含有独立电源的线电阻二端网络，对外电路来说，总可以等效为一个电压源串电阻的支路，该电压源等于原二端网络的开路电压uoc，电阻Ro等于该网络中独立电源置零后在端口处的等效电阻。aa+-bNbaa+-bb戴维南定理的证明：端口a、b处的电压为u，电流为iiaa+u-替代定Nis=bN+u-bNaa+-bb戴维南定理的证明：端口a、b处的电压为u，电流为iiaa+u-替代定Nis=bN+u-bNi0ia+叠加定理+u-Nuis=＋-bb—N中独立电源为零后的网络。u'i'i''当网络N中的电源作用时：i0ia+叠加定理+u-Nuis=＋-bb—N中独立电源为零后的网络。u'i'i''当网络N中的电源作用时：u''i''a当电流源作用时：uu'u''uoc 叠加定理：a+N-bb诺顿定理：任何一个含有独立电源的线性电二端网络，对外电路来说，总可以等效为一个电流源并电阻的电路，其中电流源等于原二端网络端口处的短路电流isc，电阻Ro等于该网络中独立电源置诺顿定理：任何一个含有独立电源的线性电二端网络，对外电路来说，总可以等效为一个电流源并电阻的电路，其中电流源等于原二端网络端口处的短路电流isc，电阻Ro等于该网络中独立电源置零后在端口处的等效电阻。诺顿定理的证明：iiaa替代定理+-bN+u-N+u-biaa叠加定理+＋-bb网络N中电源作用：i'(短路电流u'usuui'' iaa叠加定理+＋-bb网络N中电源作用：i'(短路电流u'usuui'' u''aii'i''i所R0b+u-N+u-一、电路中不含受控源的情况例4－4：求a、b端的戴维南及诺顿等效电路。i ai+++----++-b解：（1）求开路电压uocbi2163253i6一、电路中不含受控源的情况例4－4：求a、b端的戴维南及诺顿等效电路。i ai+++----++-b解：（1）求开路电压uocbi2163253i6（2）求将独立电源置零a 233o3b戴维南等效电路如图a+-b（2）求将独立电源置零a 233o3b戴维南等效电路如图a+-b（3）求短路电流a+--+b(111)u216a33233u5ui2b等效电阻R的求法同前o（3）求短路电流a+--+b(111)u216a33233u5ui2b等效电阻R的求法同前o例45RL取何值可获最大功率？最大功率是多少？a+-+-b例45RL取何值可获最大功率？最大功率是多少？a+-+-b解：先求RL左侧电路的戴维南等效电路。a（1）求开路电压:+++采用回路法-b--5i1得2)5(i12)351010(i1解：先求RL左侧电路的戴维南等效电路。a（1）求开路电压:+++采用回路法-b--5i1得2)5(i12)351010(i12)i15(i12)35所（2）求等效电阻520aRo5（3）负载R所消耗的功率LPi2)2RLLRb0LdPai+L可（2）求等效电阻520aRo5（3）负载R所消耗的功率LPi2)2RLLRb0LdPai+L可获最大功-2ui2 PbL0Ro有以下几种求解方法：（1）将网络内的独立电源置零，利用电阻的串、并联以及Δ←→Y之间的等效变换求得。（2）外加电源法aia+u-bbR0iNRo有以下几种求解方法：（1）将网络内的独立电源置零，利用电阻的串、并联以及Δ←→Y之间的等效变换求得。（2）外加电源法aia+u-bbR0iN（3）开短路法先求端口处的开路电压uoc，再求出端口处短路后的短路电流isc，那么aa+-bbR0iNN（3）开短路法先求端口处的开路电压uoc，再求出端口处短路后的短路电流isc，那么aa+-bbR0iNN二、电路中含有受控源戴维南定理与诺顿定理同样适用。开路电压uoc：求法同前，如结点法、回路法、叠加定理等。等效电阻R二、电路中含有受控源戴维南定理与诺顿定理同样适用。开路电压uoc：求法同前，如结点法、回路法、叠加定理等。等效电阻Ro：只能用外加电源法和开短路法。例4-6：求图示电路的戴维南等效电路。I+-ab解：开路电压a+28Uoc-b例4-6：求图示电路的戴维南等效电路。I+-ab解：开路电压a+28Uoc-b等效电阻:外加电源法I+-a+U5I2I3IU-bU I等效电路如图a+等效电阻:外加电源法I+-a+U5I2I3IU-bU I等效电路如图a+-b例4-电路如图所示，求ab左侧电路的戴维南等效电路。电流源Is2吸收的功率。a+IU-b例4-电路如图所示，求ab左侧电路的戴维南等效电路。电流源Is2吸收的功率。a+IU-b解：（1）求开路电压aa++-+--bb根据KVL可得4UUoc所Uoc解：（1）求开路电压aa++-+--bb根据KVL可得4UUoc所Uoc等效电阻Ro：用外加电源法I11a+- 因+1112所RU03I1-另：开短路法求等效电阻boaI短路电流U23所 RoIb等效电阻Ro：用外加电源法I11a+- 因+1112所RU03I1-另：开短路法求等效电阻boaI短路电流U23所 RoIb戴维南等效电路如图aI+-I2-3-b（2）戴维南等效电路如图aI+-I2-3-b（2）回原电路求得电流源Is2两端电压为简化运算，将右侧支路用电流源替代。+-+-- 1(423)22U+-+-- 1(423)22U323U2电流源Is2吸收的功率：P2U3特勒根定理§4-特勒根定理对于一个具有n个结点、b条支路的网络，假设各支路电压（uk特勒根定理§4-特勒根定理对于一个具有n个结点、b条支路的网络，假设各支路电压（uk）和支路电流（ik）取关联参考方向，则有：bukk物理意义：各支路吸收的功率之和等于零。buk(t1)ik(t2)另外有k特勒根定理具有同一拓扑图的两个网络N和，它们的支路ukuk’，支路电流为ik特勒根定理具有同一拓扑图的两个网络N和，它们的支路ukuk’，支路电流为ik考方向），则对任何时刻t，有：ik(均取关联参bukikkbku 例4-8：NR网络由纯电阻组成。已知R2＝2Ω，U1＝6V时，测得I1＝2A，U2＝2V；R2＝4Ω，U1＝10V时，测得I1＝3例4-8：NR网络由纯电阻组成。已知R2＝2Ω，U1＝6V时，测得I1＝2A，U2＝2V；R2＝4Ω，U1＝10V时，测得I1＝3A，求此时U2的值。++--解：根据特勒根定理bkbU1I1U2I2UkIkkUkIkRkIkIkRkIk因UkIkRkIkIkRkIk因U1I1U2I所由题知IU2UUI2211222UU I 211R42632(U2)102 则24互易定§4-设网络NR仅由线性电阻元件组成，该网络对外有两对端钮。互易定理1:对于图示两电路有us1122++--当时互易定§4-设网络NR仅由线性电阻元件组成，该网络对外有两对端钮。互易定理1:对于图示两电路有us1122++--当时us即电压源和电流表互换位置后，电流表的读数不变。互易定理2:对于图示两电路有u2is2112++--is当时即电流源和电压表互换位置后，电压表的读数不变。互易定理2:对于图示两电路有u2is2112++--is当时即电流源和电压表互换位置后，电压表的读数不变。互易定理3:对于图示两电路有us1is2112++ui21--互易定理中，如（a）图中的端钮1和2为同极性端，那么在图（b）中，端钮1和2互易定理3:对于图示两电路有us1is2112++ui21--互易定理中，如（a）图中的端钮1和2为同极性端，那么在图（b）中，端钮1和2也为同极性端us21例4-8：已知求212++i2i1-- 解us21例4-8：已知求212++i2i1-- 解us 224usi12u1例4-9：已知图（a）电路在电压源us1的作用下，电阻R2上的电压为u2。求图（b）在电流源is2的作用下，电流i1的值。+-+-例4-9：已知图（a）电路在电压源us1的作用下，电阻R2上的电压为u2。求图（b）在电流源is2的作用下，电流i1的值。+-+-解：方法一12++R1u--12R2利用互易定理u2ii由得1siuus解：方法一12++R1u--12R2利用互易定理u2ii由得1siuus方法二：改变电路画法，与互易定理1的电路对应。12+-+-i212+ 21R2isu-u2R2isisii而得2R12uRu22方法二：改变电路画法，与互易定理1的电路对应。12+-+-i212+ 21R2isu-u2R2isisii而得2R12uRu22§4-对偶原对偶：两个不同的元件特性或两个不同的电路，却具有相同形式的表达式。uLu§4-对偶原对偶：两个不同的元件特性或两个不同的电路，却具有相同形式的表达式。uLuii、L与C、电压源与电流源对偶元件：R与开关的开与闭等对偶变量：u与对偶电路：串联与并联、网孔与结点等。++-+--注意：“对偶”并非“等效”对偶电路的意义在于它们具有相同的数学模型。也就知道了。++-+--注意：“对偶”并非“等效”对偶电路的意义在于它们具有相同的数学模型。也就知道了。运算放大器的电路模型§5-多端元件、有源元件。一、运算放大器的电路符号aA+-+-c++ba、b为输入端，c为输出端- 运算放大器的电路模型§5-多端元件、有源元件。一、运算放大器的电路符号aA+-+-c++ba、b为输入端，c为输出端- u)0ibaA—放大倍 a为倒向输入端。b端接地，则a端接地，则b为非倒向输入端。-A+二、运放的特性运放有两个工作区：放大区和饱和区。t0饱和区饱和区t0利用运放的饱和特性作比较器放大 -A+二、运放的特性运放有两个工作区：放大区和饱和区。t0饱和区饱和区t0利用运放的饱和特性作比较器放大 ++运放工作在放大区时：其等效的电路模型为a+-+-+-b运放为单方向的差动放大器。A(ubua)受控源为运放工作在放大区时：其等效的电路模型为a+-+-+-b运放为单方向的差动放大器。A(ubua)受控源为Ri——输入电阻，很大R0输出电阻，较小 A 当时称为理想运放。-+“开环” A 当时称为理想运放。-+“开环”应用、“闭环”应用。-++具有理想运放的电路分析§5-理想运放的特征：倒向端和非倒向端的输入电流均为零，称为“虚断”倒向端和非倒向端为等位点，称为“虚短”①②例5-求uo与ui之间的关系R2iR +解：+②++具有理想运放的电路分析§5-理想运放的特征：倒向端和非倒向端的输入电流均为零，称为“虚断”倒向端和非倒向端为等位点，称为“虚短”①②例5-求uo与ui之间的关系R2iR +解：+②++-iR结点①处u①iiu (R2)iR--1++②得++-①uR10uu∴0i--R11++②得++-①uR10uu∴0i--R1为非倒向放大器（又称比例器）++++②++++--①u0---- 相当于右图中 得称电压跟随器。前后段的隔离作用。++++②++++--①u0---- 相当于右图中 得称电压跟随器。前后段的隔离作用。比较下列两图：++uR22--++++-uR1L--比较下列两图：++uR22--++++-uR1L--例5—2：加法+u2++-+++--RfRRu1RR123例5—2：加法+u2++-+++--RfRRu1RR123减法器+-++++i2--(u1u)R(u R(i)R(i)021 22RR11u)减法器+-++++i2--(u1u)R(u R(i)R(i)021 22RR11u)R2(uu(uu1221RR11微分电路RiC+-+u+0i-- RiRC0微分电路RiC+-+u+0i-- RiRC0积分电路CiR+-+-+u+i- 1RCCidtu0i积分电路CiR+-+-+u+i- 1RCCidtu0i例5—求uiR3R①1+③-②+-⑤④++++--解：结点电压法。但运放的输出端不能列KCL方程。 结点①例5—求uiR3R①1+③-②+-⑤④++++--解：结点电压法。但运放的输出端不能列KCL方程。 结点① u结点② u3u3结点③ u结点② u3u3结点③： 利用“虚短”列辅助方程1)(1(1u0iRRRR4321G2 第六正弦交流电路的稳态分析正弦一、正弦量按正弦规律变化的物理量。iI第六正弦交流电路的稳态分析正弦一、正弦量按正弦规律变化的物理量。iImcos(ti—正弦电流的振幅或最大值例如：其中：Imω—角频率。单位：弧度/秒ψi—初相角或初相位Im、ω、ψi称为正弦量的三要素iiIm2200ΨiiiiIm2200Ψii0二、相位差同频率的正弦量相位之差称相位差。若二、相位差同频率的正弦量相位之差称相位差。若u2=相位差=(ωt+ψu1)－(ωt+ψu2）=ψu1－ψu20=ψu1－ψu2>0时，称u1超=ψu1－ψu2>0时，称u1超前u2φ角度=ψu1－ψu2<0时，称u1落后u2|φ|角度=ψu1－ψu2=0时，称u1和u2同相=ψu1－ψu2=π时（或180°），称u1和u2反相=ψu1－ψu2=±π/2时，称u1与u2正交例i的表达式i0例i的表达式i0i=10cos(ωt－8.66=10cosψi，ψi=解∴i=10cos(ωt+若为虚线坐标，则ψi=i=10cos(ωt例设u=5cos(ωt+90°例设u=5cos(ωt+90°)、i=10cos(ωt-问哪个量落后？落后的角度为多少？解：φ=ψu-ψi=90°-(-150°)=240°>∴i落后u另：i=10cos(ωt-150°+360°)=10cos(ωtφ=ψu-ψi=90°-210°=-120°<∴也可以说u落后三、有效值T 0.239i2T—交流电的周期交流电：022T 2i2dtI则若0三、有效值T 0.239i2T—交流电的周期交流电：022T 2i2dtI则若01TTI称有效值，又称方均根值2i01TTU2u同0正弦交流电的有效值iImcos(ti11Ti2dtTcos2(tIImiTT001T[1正弦交流电的有效值iImcos(ti11Ti2dtTcos2(tIImiTT001T[1cos2(tIm)]dtmi20ImII正弦m2iImcos(ti)2Icos(ti所相量法的基本知一、复数ab—虚部a相量法的基本知一、复数ab—虚部a—实部Re—取实部Im—取虚部（1）代数形式aRe[Re[a一个复数可以表示在复平面上。例2=-2-03共轭复数*bAA的共轭A是=a+jb*如0a共轭复数*bAA的共轭A是=a+jb*如0a*A=a-A（2）指数形式复数反映在复平面上是条带箭头的直线，称矢量（或向量）。如上图线段的长度为A的模，为正。矢量与实轴正方向间的夹角称为的辐角：逆时针旋转取正，顺时针取负与代数形式的关系：aAbAsinAcosjAsinA(cos与代数形式的关系：aAbAsinAcosjAsinA(cosjsin)Aeecosjsin欧拉公式Ae复数的指数形式ba在四象限内取,Aa（3）极坐标形式工程上常把复数简写成A—极坐标形式ajbAeA三种形式完全相复数相等jbAeAA111111 AeA 22222复数相等jbAeAA111111 AeA 222222a1=a2，b1=b2；A1=A2，1=。ajbAeAA若复数共轭*AajbAe则复数运算（1）加减法：代数形式方便AA)j(b)121212（2）乘除法：指数或极坐标形式方便Aej(jAAA,2 1 2 A1 （2）乘除法：指数或极坐标形式方便Aej(jAAA,2 1 2 A1 Aej(1e , AeA2 212AA222二、正弦量的相量表示复指数j(tUmcos(tu)jUmsin(tuUmeuj二、正弦量的相量表示复指数j(tUmcos(tu)jUmsin(tuUmeuj(t uuUmcos(tu)Re[Ume正弦电压]]Re[Ume]ReuuUm jtRe其——振幅相相量mU注意：相量≠正弦量，即2cos(t45)i1例6-写出电流211sin(t120)5解2cos(t45)i1例6-写出电流211sin(t120)5解的相量。1i2 2sin(t120)2cos(t30)1130263例6-写12f2cos(2ft50)2cos(314t602cos(314t50解 2cos(314t 例6-已1352cos(314t ，求6 iiR 2cos(314t 例6-已1352cos(314t ，求6 iiR 解eR 2Iejt]Ri112ee22(II)ejtRe12II所12550j86.6190.5 140.5j196.6241.6ii12cos(314t基本定律与基本元件的相量形式一、KVL、KCL的相量形式bbukk1bi基本定律与基本元件的相量形式一、KVL、KCL的相量形式bbukk1bi时kkb相kkk二、元件R、L、C在正弦电路中1．电阻元件1）R中的瞬时电压与电流 2IRcos(ti所如则2URcos(tu)2IRcos(ti所如则2URcos(tu)UR=cos(ti2RIuR与iR同相，即Ψu=Ψi +R0-Ψu2）R中的电压相量与电流相量UR+R-RΨu=由瞬时表达式知：I RUR2）R中的电压相量与电流相量UR+R-RΨu=由瞬时表达式知：I RUR RIRR相量形式仍满足欧姆定律R2．电感元件1）L中的瞬时电流与电压+0-2．电感元件1）L中的瞬时电流与电压+0-Lu（关联LL2ILcos(ti 如 cos(t )LuLLu2ILsin(t2ILcos(ti 如 cos(t )LuLLu2ILsin(ti)]（a）UL2LILcos(t所90（b）i电压超前电流u2）L中的电压相量与电流相量 LLiUL i90L 称为感抗XLL LLLΨuΨ 称为感抗XLL LLLΨuΨi-3．电容元件1）C中的瞬时电压与电流Ci（关联c2Uccos(tu 如2I cos(t)C cci2CUc 2CUcsin(tu2I cos(t)C cci2CUc 2CUcsin(tucos(t90+0C- CIc或Uc所以：（a）Ψu=Ψi－90°电压滞后电流（b）2）C中的电压相量与电流相量c+c ΨiΨu-Uc 90ccicuc112）C中的电压相量与电流相量c+c ΨiΨu-Uc 90ccicuc11ccc X称为容抗c4．相量与时域的对应关系：（正弦电路中 RLuLLLdCiccc1L4．相量与时域的对应关系：（正弦电路中 RLuLLLdCiccc1LiuLLLL乘 CicjC阻抗与导1统一形式URRLLcc11阻抗与导1统一形式URRLLcc11统一形式IRRLLccR称Z为元件的阻抗，Y为元件的导纳；导纳的单位：西门子阻抗的单位：欧姆推广到一个不含独立电源的网络UIIUU ZZ则II ZZcosjZsinZR即实部R—电阻|Z|—阻抗的模虚部X—电抗θ—阻抗+++ RUU ZZ则II ZZcosjZsinZR即实部R—电阻|Z|—阻抗的模虚部X—电抗θ—阻抗+++ R-Z- - 电阻元件：Z电感元件：Z=jωL1Z电容元件：IY电阻元件：Z电感元件：Z=jωL1Z电容元件：IYG同iuU实部G—电导虚部B—电纳ψ—导纳|Y|—导纳的模例6-求图示RLC串联电路的等效阻抗++--++R+ U-xc--1解例6-求图示RLC串联电路的等效阻抗++--++R+ U-xc--1解RLc1(RjLX)]Ij(Lc1ZRjLC)Rj(X Xc)R所以①②③当X=XL－Xc=0时θ=Ψu－Ψi=0，电路呈阻性当X=XL－Xc>0时θ=Ψu－Ψi>0①②③当X=XL－Xc=0时θ=Ψu－Ψi=0，电路呈阻性当X=XL－Xc>0时θ=Ψu－Ψi>0，电路呈感当X=XL－Xc<0时θ=Ψu－Ψi<0，电路呈容相应的相量图ULULΨΨu=ΨuLRiΨcc（a）XL=Xc，=（b）XL>Xc，>（c）XL<Xc，<注意：Ψu、Ψi是电压、电流相量与正实轴之间的夹角，而θ是电压与电流相量之间的夹角，且超前时取正，反之取负。U与UR、UL、之间的关系UUUUU注意：Ψu、Ψi是电压、电流相量与正实轴之间的夹角，而θ是电压与电流相量之间的夹角，且超前时取正，反之取负。U与UR、UL、之间的关系UUUUURXRLcZ与R、XL、Xc之间的关系cX(XRR2Z2UX（a）电压三角形R（b）阻抗三角形RLC并联电路+BcGL R- GLcRRLC并联电路+BcGL R- GLcR11jCLGjBcBLGY1jc1GjBBLcLY1jc1GjBBLcLRGjB1B=C容纳B=B—电纳感cL=|Y|导纳的模—导纳角①当B=BcBL=0时，=iu=0,呈阻性②当B=BcBL>0时，③当B=BcBL<0时，电流超前电压,呈容性电流滞后电压,呈感性相量图GΨcIuΨLiΨIcUIcLGGu，<（相量图GΨcIuΨLiΨIcUIcLGGu，<（c）B<cL（b）Bc>BL，>L（a）Bc=BL，=是电流与电压间的夹