广东佛山一中2023年高二年级上册第一次质量检测数学试题含答案

佛山一中2023-2024学年第一学期

高二级第一次教学质量检测试题数学

2023年10月

本试卷共22小题，满分150分，考试时间120分钟。

注意事项：

1.答题前，考生务必用黑色笔迹的钢笔或签字笔将自己的姓名、考号填写在答题卷上。

2.每小题选出答案后，用2B铅笔把答题卷上对应题目选项的答案信息点涂黑；如需改动，

用橡皮擦干净石，再选涂其他答案，答案不能答在试卷上。非选择题必须用黑色字迹的钢笔或签字

笔作答，答案必须写在答题卷各题目指定区域内相应位置上：如需改动，先划掉原来的答案，然后

再写上新的答案；不准使用铅笔和涂改液。不按以上要求作答的答案无效。

3.作答选做题时，请先用2B铅笔填涂选做题的题组号对应的信息点，再作答。漏涂、错涂、

多涂的，答案无效。

一、单选题（本大题共8小题，共40分。在每小题列出的选项中，选出符合题目的一项）

1.已知两个向量加=（-2,m,2）,若。〃B,则m的值为（）

A.4B.-2C.2D.4

2.若｛Z,b,2｝是空间的一个基底，则也可以作为该空间基底的是（）

A.bc,b,-b—cB.a,a+b,a-b

C.a+b,a—b,cD.a+b,a+b+c,c

3.“哥德巴赫猜想”是近代三大数学难题之一，其内容是：一个大于2:的偶数都可以

写成两个质数（也称为素数，是一个大于1的自然数，除了1和它自身之外，不能被其

它自然数整除的数叫做质数）之和，也就是我们所谓的“1+1”问题.它是1742年由数学家

哥德巴赫提出的，我国数学家潘承洞、王元、陈景润等曾在哥德巴赫猜想的证明中做

出过相当好的成绩.若将6拆成两个正整数的和，则加数全部为质数的概率是（）

A.-B.-C.-D.-

34-26

4.已知直线国x+y—2=0,则（）

A.直线2的倾斜角为?B.直线/的斜率为旧

C.直线，的一个法向量为元=（1，8），D.直线2的一个方向向量为讶=（一百，3）

5.已知平行六面体ABCD-ABCD中，AB=4,AD=3,AA'=5,ZBAD=90°,^BAA'=

^DAA'=60。.则AC'的长为（）

A.^85B.V9,C.120.2回

6.在空间直角坐标系中，点A（l,2,3）关于y轴的对称点为点B,则点C（3,0,l）到直线AB•的

距离为（）

45.—C.—D.6

55

7.二面角的棱上有A,B两点，直线AC,BD分别在这个二面角的两个半平面内，且

都垂直于AB,已知AB=2,AC=3,BD=4,CD=内,则该二面角的大小为（）

A.45°B.60°C.120°D.150°.

8.《九章算术》中，将四个面都为直角三角形的四面体称之为鳖膈.如图，在鳖埼

A-BCD中,AB，面BCD,.AB=CD=1,BC=V2.BD=b，则下列选项中，不正确的是

A.平面ABCJ_平面ACDyK

B.二面角D-AB-C的余弦值为

C.AD与平面BCD所成角为30°

D.三棱锥A-BCD外接球的表面积为兀...二

二、多选题（本大题共4小题，共20分。在每小题有多项符合题目要求）

9：下列关于空间向量的命题中，正确的有（）

A,直线Z的方向向量江=（0.3,0）,平面a的法向量是G=（0,-5,0）,则l//a;

B.若五,b,c是空间的一组基底,则向量益++a也是空间一组基底；

C.若非零向量2b,济茜足aLb,bld则有d〃演

D.若函函沆是空间的一组基底，且彷=巳而+，砺苑则A,B,C,D四点共面.

10.甲、乙两队进行排球比赛，采取五局三胜制（当一队赢得三场胜利时，该队获胜，

比赛结束）.根据前期比赛成绩可知在每一局比赛中，甲队获胜的概率为：，乙队获胜的

概率为9.若前两局中乙队以2：0领先，则（）

A.甲队获胜的概率为白B.乙队以3：0获胜的既米为:

273

C.乙队以3：1获胜的概率为：D.乙队以3：2获胜的概率为±

99

11.如图,在正三棱柱ABC-ABC中，若AB=BBi=2,则（）

A.三棱锥B-ABC的体积为学B.三棱锥B-ABG的体积为2K

C.点C到直线ABi的距离为当D.点C到直线ABi的距离为.V14

第II婷明第12跳图第15题图

12.如图，己知正方体ABCD-ABiGDi的棱长为2,P为空间中一点，寿=xAA+yAB+

z而，则()

A.当％=z=；,y=0时，异面直线BP与CiD所成角的余弦值为

26

B.当x=y=l,ze[O,l]时,三棱锥A-PBC的体积为

C.当％=±y=l,ze[0，1]时；有且仅有一个点P,使得AC_L平面ABF

D.当y=O,x=ze[O,l]时，异面直线BP和CQ所成角的取值范围是外

三、填空题(本大题共4小题，共20分)

13.已知空间向量2=(1,-2,3),则向量d在坐标平面xOy上的投影向量是.

14.倾斜角是135°,在y轴上的截距是3的直线的一般方程为.

15.如图，在棱长为1的正四面体(四个面都是正三角形)ABCD中，M,N分别为BC、

AD的中点，则直线AM和CN夹角的余弦值为.

16.晶体结构中有一类为菱方晶系，菱方晶系是指从一个顶点出发等长且互相所成角两

两相等的线段形成的平行六面体，如图所示.若一种金n__________

属的菱方晶系结构a=60。，为研究此金属的性质，需加彳尸，।

计算出侧棱AAi与底面ABCD的所成角的余弦值，则////

此余弦值为_.,存,

・■■

四、解答题(本大题共6小题，共70分。解答应写出文字说明，证明过程或演算步骤)

17.(本小题10分)已知空间三点A(2,-5,1),B(2,-2,4),C(1,-4,1).

⑴求向量屈与方的夹角；

⑵若(荏-kAC)L(AB+左左),求实数k的值a

18.(本小题12分)已知平面内两点A(8,-6),B(2,2).

(1)求过P(2,-3)点且与直线AB平行的直线/的方程;

(2)求线段AB的垂直平分线的方程.

19.(本小题12分)数学核心素养是指在数学学习和应用的过程中逐步形成和发展的关于

数学课程目标的集中体现，是具有数学基本特征的思维品质、关键能力以及情感、态

度与价值观的综合体现.数学核心素养包括数学抽象、逻辑推理、数学建模、直观想象、

数学运算和数据分析六个方面.某学校高一、高二、高三学生分别有720,1080,1200

人，现采用分层抽样的方法，从该学校上述学生中抽取250人调查学生数学核心素养的

发展情况.

(I)应从高一、高二、高三学生中分别抽取多少人？

(II)抽取的250人中，核心素养六个方面中至少两项不达标的学生有6人，分别记为A,

B,C,D,E,F.具体情况如下表，其中“。”表示达标，“入”表示不达标.现从这6人中

随机抽取2人接受采访.

数学核心素养ABCDEF

数学抽象XXOXOX

直观想象OOXOXX

逻辑推理OOOXOO

数学运算XXOOXX

数学建模OOXOOO

数据分析XXOOOX

(1)试用所给字母列举出所有可能的抽取结果；

(2)设M为事件“抽取的2人不达标的项目中至少有一项相同：，求发发生的概率20(本小

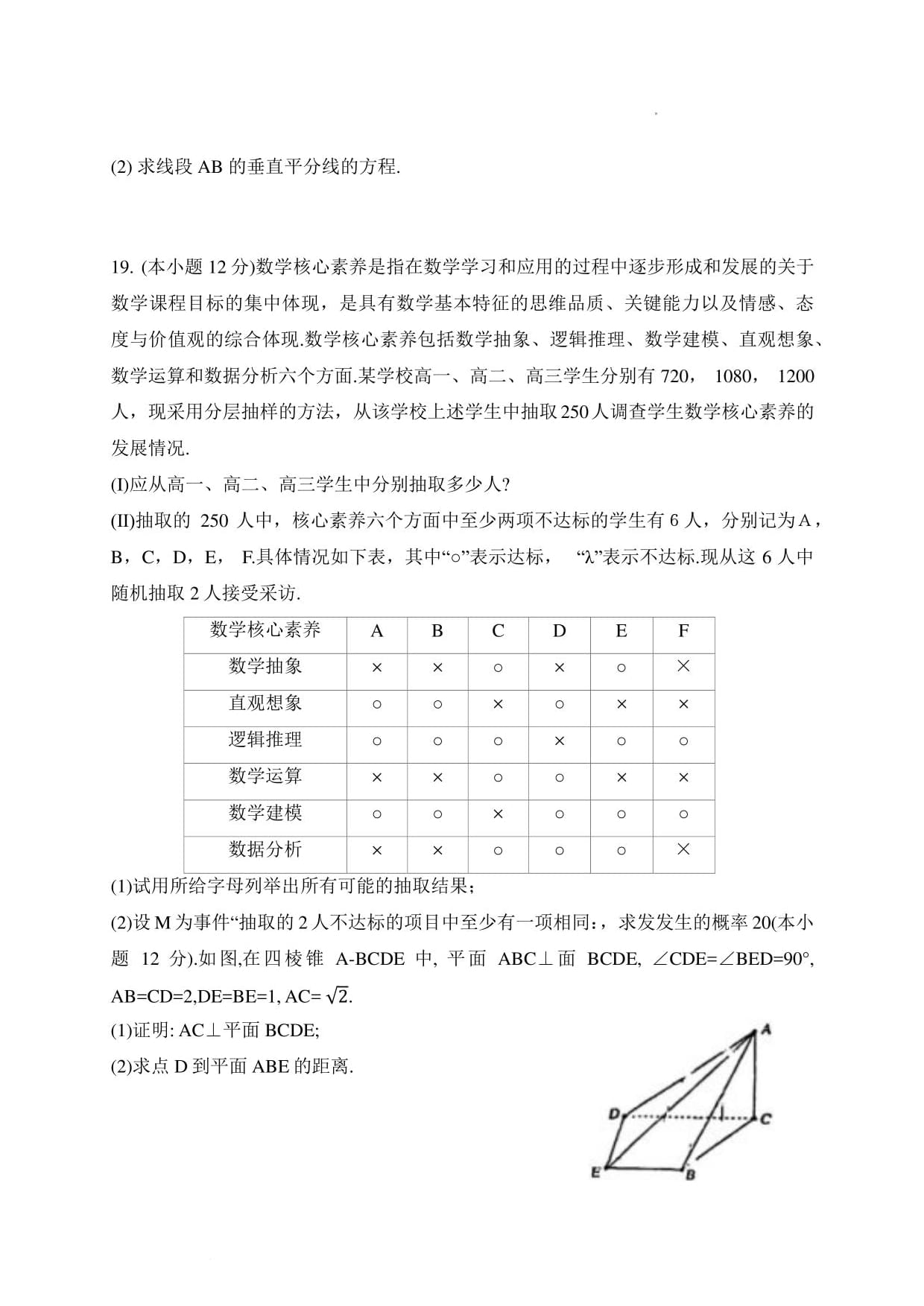
题12分).如图，在四棱锥A-BCDE中，平面ABC,面BCDE,ZCDE=ZBED=90°,

AB=CD=2,DE=BE=1,AC=V2.

(1)证明：AC,平面BCDE;/A

(2)求点D到平面ABE的距离.〃]

D

21.(本小题12分)如图所示，四边形ABCD是直角梯形，NABC=NBAD=9()o,SA，平

面ABCD,SA=AB=BC=2,AD=1.

(1)求SC与平面ASD所成角的正弦值；

(2)求平面SAB和平面SCD所成角的余弦值..

22.(本小题12分)已知三棱柱AIBCLABC中,/B=4C=&,BC==2,点M为CG

的中点，丽=2丽

⑴求证:AC〃平面BMN;

(2)条件①：直线ABi与平面BBCC所成的角为30。,条件

②：NBiBC为锐角，三棱锥Bi-ABC的体积为¥

在以上两个条件中任选一个，补充在下面的问题中，

并解决该问题：

若平面ABC,平面BBCC,，求平面BMN与平面BBiC.C所成的锐二面角的余

弦值.(注：在横线上填上所选条件的序号，如果选择多个条件分别解答，按第一个解答

计分.)

佛山一中2023-2024学年第一学期高二级第一次质量检测试题

答案

123456789101112

DCADACBDBDABACABD

13.(1.-20114x+v-3=015.-16.”

33

8.【答案】。解：对于47IBLT面OCD,8Cu平面8CD,8Du平面BCD,

所以4818C,4B1BD,可得4c=VA8?.+CB?=C，AD=yjAB2+BD2=2.

则有4C2+C。2=4D2,...4c，cD.•.•4B_L平面BCD,CZ?u平面BCO,..4E1CD,

又48cAe=4,48,4。<3平面48乙；.。。1平面/8a又CDu平面4CD,

:.平面48CJL平面4C。，故彳正确：

对于8,F8，平面BCD,8Cu平面BCD,BDc^BCD,^.ABLBD,AB±CB,

.,•/。8。就是二面角0-48—。的平面角，又••AB=CO=1,fiC=<2.5D=<3.

ABC2+CD2=BD2,•••BCLCD,在直角三角形BCD中，cosMBD=^=半=与故6正确;

对于C.平面8CD,•••4。与平面BCD所成角为UDB,

在直角三角形48。中，48=1,BD=6,所必。=2,所以々4DE=3(T,故C正确；

对于O,取>4。的中点为^1MA=MB=MC=MD=1.、

所以三棱电4-BCD外接球的半径为1,其表面积S=4M?2=4”，故。错误.

故选。.

12.I答案】ABD【解答】解：对于4连接8a.AD,.

I、

因为方=£i。夕方+z万，所以当x=z=；,y=0时，P为4D；的中点,

.2

而4BCD-44GA是棱长为2的正方体，因此连接40，则一是4。的中点•

取4G的中点。连接HZBO.BtD,.则。也是qA的中点.如图：

则产O//CQ,所以NJP。或其补角即异面直线而与G。所成的角.

因为在正方体488—444A中，6耳平面44GA,4"匚平面

44G0，所以BB'LBPi，因此(何=加,同理可得：

BP=y/6,而PO=：GD=五,所以cosZBPO=IP。

2，~BP=~6'即异面直线勿与G。所成

高二口重一次质■检泅试顾教学堂超答卷WlW#«<JT

角的余弦值为且，故ZI正确；

6

对于8.因为万=*五，+y布+z石，且是正方体,所以当x=y=i,

ZW[OJ时，

AP-AAt+AB+zAD=AB]+zAD,即4，=z/D(ze[0J]),

因此用一Z后一Z属1Qg。4]),所以点，的轨迹为线段AG，即点八在线段片G上(包括

端点)，因此/_；>.=§446”“：U2x]x22=：,故8正确；

对于C.因为方=x7彳+3,方+Z而，且4BCD-4BCR是正方体,所以当x=g,y=\,

zw[O,l]时,万=4五+而+z否(zw[O,l]),如图：取BB、、CG的中点分别为EF.则

2

AP——AAy+AB+zAD(zG[0,1])=AE+zAD{zG[0,1]),-----------

因此而=2而=2丽(ZW[0JD，所以点"在线段炉上(包B\f：\\'

括端点).在正方体数CD-4sleQ中，#13；'卜'、、

因为彳4J.平面4耳GA，BRU平面4B£D-所以,

例_L4A，而耳〃JL4G，"c4G=4,4,4G<="c,

平面小G。，因此耳&J■平面44GC,而4。u平面MG。，所以与〃_L4C

同理可得4R_L4C.因为c4A=D\,AD,.qRu平面/片乌,所以J.平面4耳R.

因此若存在点自，使得4CJ■平面彳片尸，则平面/用尸与平面重合.

显然当点。在线段炉上时，平面/男尸与平面4BR不重合，

所以存在点只使得4CJ■平面4S『不成立，故C错误；

对于。.因为方=xAA,+yAB+zAD,且ABCD-4耳GA是正方体.

所以当y=0,x=ze[0,l]时，

=x(AA^+AD)=xAD,(x€[0,1]).，申^----------才

因此点。的轨迹为线段，即点户在线段应上(包括端点).二、F/

以4为坐标原点，4耳，44，4/所在直线分别为％y,Z轴，/''LV

，人-—-----/

建立空间直角坐标系如下图：.///

高二级第一次质置检测试理数学学科答案第2页共8页

则

8(2to,2),C,(2,2,0),D(0.2,2),D,(0,2,0),/(0.0,2),

因此杀=(-2,0,2),=(0.2,-2),丽=(2,0,0).

因为而==(0,2A,-2JC)(XW[0,1])，

所以丽=（-2«2XL2X）（X40,1］）.设异面直线8"和GO所成角为夕｛0,1），

则8s”|cos<m/卡昌瑞=应聚2?

因为XG［OJ,所以当x=l,即点。与R重合时，cos^=—,因此e=9

,22

.8s8=--=====

当xw[0,i)时,令r=i-X,则0</41,因此q.Ji+2(1—)2

'3、

因为由对勾函数的图象知：函数，=2/+：-4=2t+j-4（，e（0』）是减函数,

3

-

+2

所以函数y=〃+3-4=27-4（/w（05）的值域为［1,加）

因此°<Z+3-J所以°<cos小孝’因此9"会

综上所述，异面直线分和G?所成角的取值范围是中守,故。正确,故选：ABD.

16.解：如图所不：

国1作41。1平面4BCD,AiElAD.AiFl.AB,连接

OE,OF,OA.则"ME=^AtAF=AEAF=a=60',

"M。为侧棱与底面48CD所成的角，

因为4。，平面ABCD,所以乙01AE,又

40n4iE=&,所以4EJ■平面&E0,贝!!4E'J.E。，

同理入尸。，因为尸，所以

51Rt/41AEwRt，414

4iE=4A则Rt4410E三Rta4］。尸，所以。E=0尸，则点。在/D4B的角平分线上，所以

==

Z.EAOf30",设=m,则=AtA•CQsa=1m»所以cos4遇。=

器=.苧，故答案：建

/

17解：⑴由已知得：/1B=(O,3,3),衣=(一1,1,0),2分

ABAC0x(-l)+3xl+3x0

cos<AB,AC>=

I祠码-Vo+3J+3fjr+l+O；：2'4分

又向量夹角范围是[0,”],所以向量方与AC的夹角为60；....................5分

(2)在-kAC=(k3-k,3),AB+kAC=(-k,3+〃；3),.

(AB-kAC)1(AB+kAC).：.(AB-kAC)-(AB+kAC)=0..................8分

二kx(-k)+(3-K)x(3+Z:)+3x3=0,解得k=3或k=-3.

二实数4的值是3或-3.：....................10分

、,-6-24

18.解：0)：号,=万==一二，

4

过尸(Z—3)点且与直线48平行的直线/的斜率为......................3分

3

4

其方程为：J+3=--(X-2),化为4x+3y+l=0....................6分

(2)线段48的中点为(等，二^2),即(5,-2),..................8分

22

3

••・线段AB的垂直平分线直线的斜率卜=二、.....：•...........10分

4

3

的垂直平分线直线方程为y+2=：(x-5),化为3x-4y-23=0;...........12分

4

19.解：(I)由已知，高一、高二、高三学生人数之比为6:9:10,...........2分

由于采取分层抽样的方法从中抽取250位学生，

因此应从高一、高二、高三学生中分别抽取60人，90人，100人；............4分

(nXD从已知的6人中随机抽取2人的所有可能结果为

{A,B},{A,C},{A,D},{A,E},{A,F}\{B,C},{B,D},{B,E},{B,F}.{C.D},{C.E}.

{C,F},{D,E},{D,F},{E.F}共15种；............8分

(2)由表格知，符合题意的所有可能结果为{48},,{40,{4身，{4产},

/{B,F},{C,E},{C,F},尸},{瓦用共11种，..........TO分

所以，事件〃发生的概率尸(M)=£.……:........12分

20.(I)取CO中点G,连结BG.'：NCDE=ZBED=90°,：.BE//CD.

又8=2,BE=I,'：BE±DG,二四边形DE3G为矩形，..........2分

：.BG=DE=\,ZBGC=90°,XGC=-CD=1.:.BC=&.又/C=及，AB=2,二彳*=

2

4O+BC2,即/C_18c......................4分

又二•平面XBCJ■平面BCDE且交线为BC,

ZCu平面Z5C,二/CJ•平面BC0E................-♦•…6分

(2)以。为原点，DE、OC分别为x轴、y轴,过。作垂直的

平面的直线，为z轴，建立空间直角坐标系如图.

则D(0,0,0),C(0,2,0),^(0,2,72).5(1,1,0),£(1,0,0^

，.豆=(-120),丽=(0,1,0),丽=(1,0,0)：……8分

设平面彳BE的法向址为n=(x,y,z),则

n-£A=0.—x+2y+y/2z=0

,一一••<

n.EB=01/=0

令z=l得〃=(嫄,0,1)......................10分

Y_

设。到平面/BE的距离为，则"二匚^二》:二•.............12分

〃63「

21.解：⑴如图建系，5(0,0,2),C(2,Z0),D(l,0,0),

SC=(2,2,-2)..................2分

•••ZB_L平面SAD,故平面ASD的一个法向・为

施=(0,2,0),..................4分

设SC与平面4S。所成的角为心则sin，=焉鬻=乎，

I

即SC与平面4SZ?所成角的正弦值为手；.....................6分

(2)平面的一个法向■为：而=(L。,。)，

vSC=(2,2,-2),SD=(l,0,-2)......................8分

设平面SCD的f法向珏为n=(x,j,z),

高二级第一次质量检测试短数学学科答案第5页共8页

SCn=Opx+y-z=O

由《一.得

SDn=Ox-2z=0

令z=1可得平面SCD的一个法向量为n=(2,-1,1),.....................10分

显然，平面阳8和平面SCO所成角为锐角，设为a.

贝I]cosa=1"-=,

|m||n|3

即平面第8和平面SCO所成角的余弦值为理

12分

3

22(1)证明：如图：延长8A/交彳4于e连接PM.

,因为几何体44G-ABC是三棱柱,

所以四边形/4耳3是平行四边形，而4N=2Mf,

APAN

m因i此l==.

心NBt2,

即飒所以「是的中点.又因为点〃为CG的中点，四边形小是平行

22.••

四边形,2分

所以以，二屿，因此四边形尸4GM是平行四边形，所以4G//PM.

又因为4GC平面8%V,PMu平面8MM所以4G〃平面3MN.4分

(2)解：选择条件①，解答过程如下:

取8c的中点。连接49、BQ.因为4B=4C=&，BC=BBr2,

所以AB2+AC2=BC2,因此4ABe是以8c为斜边的等腰直角三角形.

所以4O_L3C且O/=0=OC=L

又因为平面4JCJL平面3qCQ,两个平面交于直线夕CAO±BCtdOu平面48C

所以40J_平面B4G。，因此4B0为直线与平面所成的角，所以440=301

因为ZOJ■平面AB。。，又&Ou平面,所以,

在RtA/4。中，因为04=1,勿0=30,所以BQ=百.......................6分

又因为80=1,BQ=芯,BBt=2,

所以BO+BO=B耳,因此80JLBQ.以。为坐标原点，以丽、西、分别为*轴、y轴、

z轴正方向，建立空间直角坐标系如下：''

高二级第一次质量检测试题数学学科答案第6页夬8页

则｛(0,0,1),8(1,0,0),C(-l,0.0).B,(o.Ao).

所以尸M=/6=(-1,O,-l),比=(-2,0,0).

西=(-1,6,0)

丽=前+两=前+；西

=(-2,0,0)+与=V奈。).......8分

设平面8MN的法向量为所=(玉,必,马)，

贝”一，即，