九年级数学上册第23章解直角三角形232解直角三角形及其应用(第二课时)课件(新版)沪科版

23.2解直角三角形及其应用第2课时第二十三章23.2解直角三角形及其应用第二十三章(1)三边之间的关系:a2＋b2＝c2（勾股定理）解直角三角形的常用等量关系(2)锐角之间的关系:∠A＋∠B＝90º(3)边角之间的关系:ACBabc(1)三边之间的关系:a2＋b2＝c2（勾股定理）解直角三角

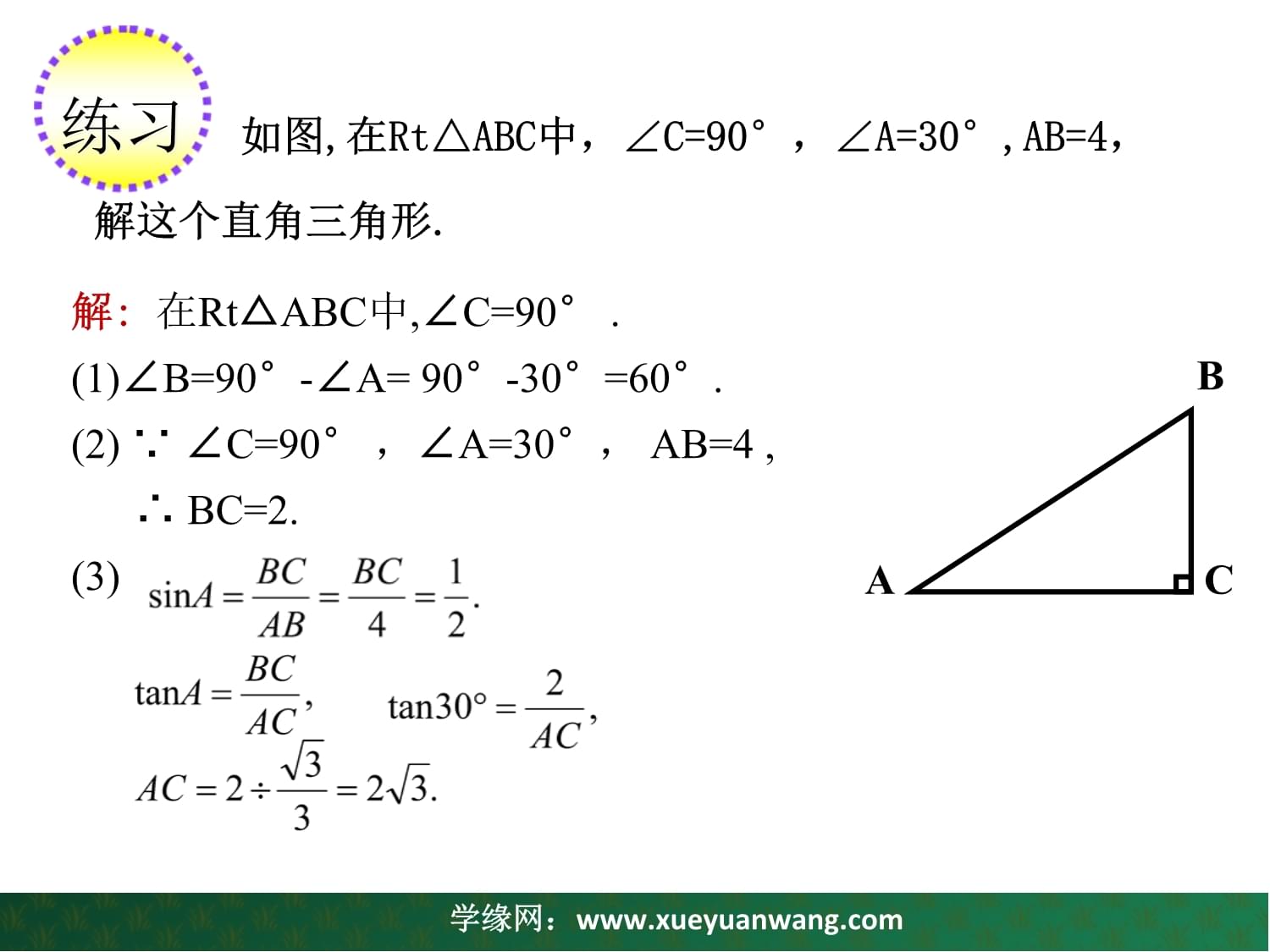
如图,在Rt△ABC中，∠C=90°，∠A=30°,AB=4，解这个直角三角形.

ABC解:在Rt△ABC中,∠C=90°.(1)∠B=90°-∠A=90°-30°=60°.(2)∵∠C=90°

，∠A=30°，AB=4,∴BC=2.(3)练习如图,在Rt△ABC中，∠C=90°，

举行升旗仪式时，全体师生肃立行注目礼，少先队员行队礼。

旗杆长为多少？举行升旗仪式时，全体师生肃立行注目礼，少先队员行队礼。

在视线与水平线所成的角中，视线在水平线上方的角叫做仰角。视线在水平线下方的角叫做俯角。强调：仰角与俯角都是视线与水平线所成的角。水平线铅垂线视线仰角视线俯角在视线与水平线所成的角中，强调：水平线铅垂线视线仰角视

如图,一学生要测量校园内一棵水杉树的高度，他站在距离水杉树8m的E处，测得树顶的仰角∠ACD=52°，已知测角仪的架高CE=1.6m．问树高AB为多少米？(精确到0.1m)

你知道怎样算出树高吗？EB1.6m8m?52°DAC例1如图,一学生要测量校园内一棵1.6m8m?52°DAECB解：Rt△ACD中，∠ACD=52°，CD=EB=8m.又DB=CE=1.6m，得AB=AD+DB=10.2+1.6=11.8（m）答：树高约为11.8m.1.6m8m?52°DAECB解：Rt△ACD中，∠ACD1.如图,飞机飞行的高度AB=1000m,从飞机上测得地面着陆点C的俯角为18°，求飞机到着陆点的距离AC的值.(精确到1m)ABC18°解：由题意得∠C=18°答：飞机A到着陆点AC的距离约为3236m.1.如图,飞机飞行的高度AB=1000m,从飞机上测得ABC

2.如图，沿AC方向开山修路．为了加快施工进度，要在小山的另一侧的E处同时施工。如果从AC上的一点B，使∠ABD=140°，BD=520m,∠D=50°,那么开挖点E离D多远正好能使A，C，E成一直线（精确到1m）50°140°520mABCED∴∠BED=∠ABD－∠D=90°答：开挖点E离点D334m正好能使A，C，E成一直线.解：要使A、C、E在同一直线上，则∠ABD是△BDE

的一个外角.2.如图，沿AC方向开山修路．为了加快施工进度，要在小同时量得CD=50m.已知测角器高1m,问电视塔的高度为多少米？(精确到1m)．

如图某校九年级学生为了测出当地电视塔的高度AB，因为不能直接到达塔底B处,他们采用在发射台院外与塔底B成一直线的C，D两处地面上，用测角器测得电视塔顶A的仰角分别为45°、30°,CBD30°45°C1B1AD1例250m同时量得CD=50m.已知测角器高1m,问电视塔的高度为多CBD30°45°C1B1AD1（1）这个图形中有哪几个直角三

角形？（2）这些直角三角形之间有何关系？分析50m（3）在每个直角三角形中用哪种边角关系才能与已知建立起等量关系？CBD30°45°C1B1AD1（1）这个图形中有哪几个直解：设AB1=xm.

在Rt△AC1B1中，∠AB1C1=90°∠AC1B1=45°得C1B1=AB1=x

在Rt△A1D1B1中，∠AB1D1=90°∠AD1B1=30°得解方程，得答：电视塔的高度约为69m.CBD30°45°C1B1AD150m解：设AB1=xm.解方程，得答：电视塔的高度约为69m.C如图，某直升机于空中A处测得正前方地面控制点C的俯角为30°；若航向不变，直升机继续向前飞行1000m至B处，测得地面控制点C的俯角为45°.求直升机再向前飞行多远与地面控制点C的距离最近(结果保留根号).ACBD提示：过C作CD⊥AB，垂足为D.在△ACD和△BCD中利用解直角三角形知识得CD=500()m.如图，某直升机于空中A处测得正前方地面控制点C的俯角为30°指南或指北的方向线与目标方向线构成小于90°的角,叫做方位角.如图：点A在O的北偏东30°点B在点O的南偏西45°（西南方向）30°45°BOA东西北南方位角介绍:指南或指北的方向线与目标方向线构成小于90°的角,叫做方位角

如图，一艘海轮位于灯塔P的北偏东65°方向，距离灯塔80海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东34°方向上的B处，这时，海轮所在的B处距离灯塔P有多远？（精确到0.01海里）65°34°PBCA例3如图，一艘海轮位于灯塔P的北例3

如图，一艘海轮位于灯塔P的北偏东65°方向，距离灯塔80海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东34°方向上的B处，这时，海轮所在的B处距离灯塔P有多远（精确到0.01海里）？解：如图，在Rt△APC中，PC＝PA·cos（90°－65°）＝80×cos25°≈80×0.91=72.8在Rt△BPC中，∠B＝34°当海轮到达位于灯塔P的南偏东34°方向时，它距离灯塔P大约130.23海里．65°34°PBCAcos∠APC＝PC÷PA例3如图，一艘海轮位于灯塔P的北偏东65°方向，距离灯塔8

1.在解直角三角形及应用时经常接触到的一些概念------

2.如何将实际问题向数学模型转化------

我知道

通过这节课的学习你有哪些收获与体会？仰角,俯角;方位角

解直角三角形1.在解直角三角形及应用时经常接触到的一些归纳利用解直角三角形的知识解决实际问题的一般过程是：（1）将实际问题抽象为数学问题（画出平面图形，转化为解直角三角形的问题）；（2）根据条件的特点，适当选用锐角三角形函数等去解直角三角形；（3）得到数学问题的答案；（4）得到实际问题的答案．归