立体几何中的向量方法(３)_第1页
立体几何中的向量方法(３)_第2页
立体几何中的向量方法(３)_第3页
立体几何中的向量方法(３)_第4页
立体几何中的向量方法(３)_第5页
已阅读5页，还剩7页未读， 继续免费阅读

下载本文档

版权说明：本文档由用户提供并上传，收益归属内容提供方，若内容存在侵权，请进行举报或认领

文档简介

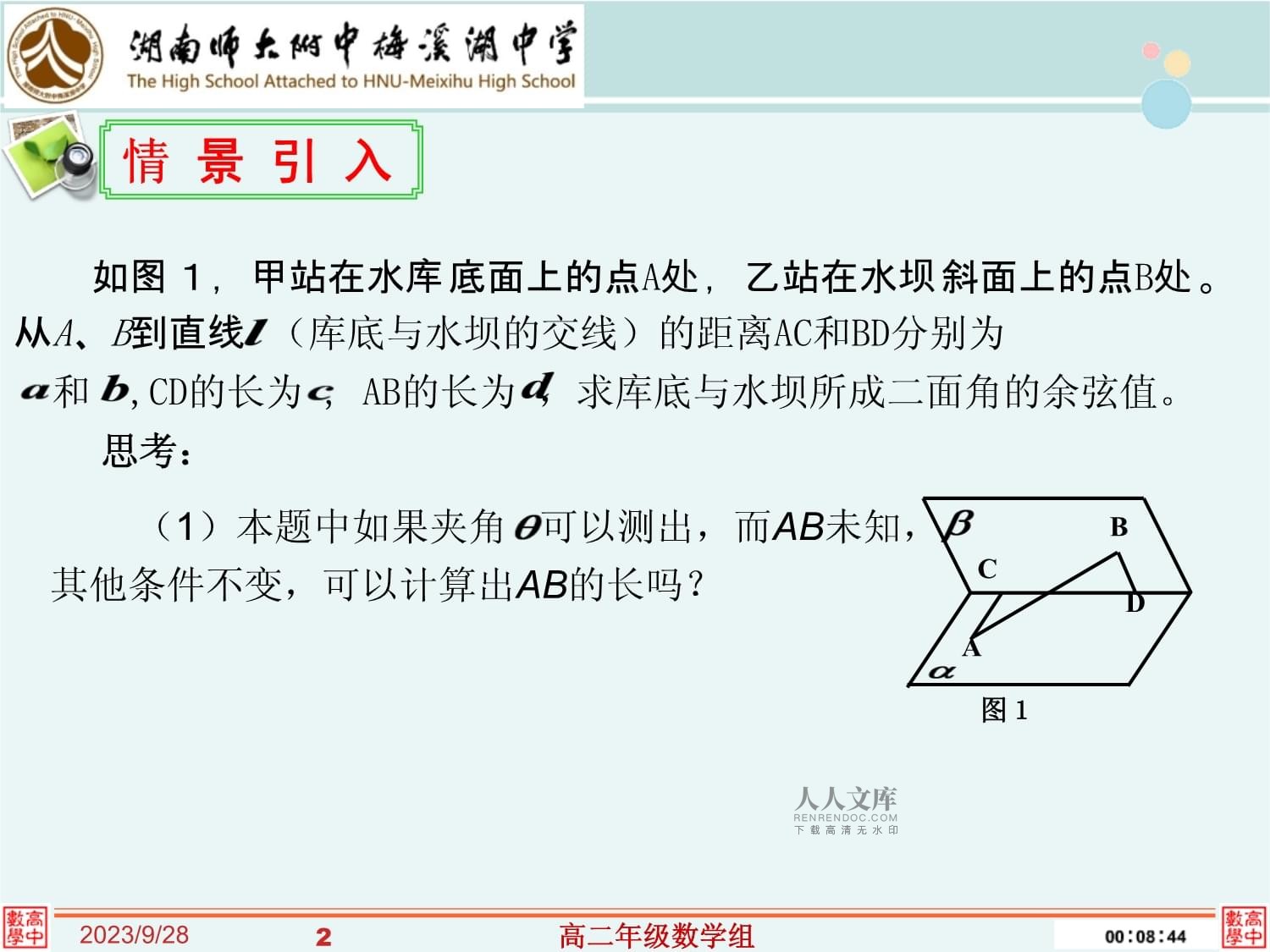
第三章空间向量与立体几何323立体几何中的向量方法（3）如图１，甲站在水库底面上的点A处，乙站在水坝斜面上的点B处。从A、B到直线（库底与水坝的交线）的距离AC和BD分别为和,CD的长为,AB的长为，求库底与水坝所成二面角的余弦值。ABCD图１

情景引入

思考：

（1）本题中如果夹角可以测出，而AB未知，其他条件不变，可以计算出AB的长吗？（2）如果已知一个四棱柱的各棱长和一条对角线的长，并且以同一顶点为端点的各棱间的夹角都相等，那么可以确定各棱之间夹角的余弦值吗？A1B1C1D1ABCD

（3）如果已知一个四棱柱的各棱长都等于，并且以某一顶点为端点的各棱间的夹角都等于，那么可以确定这个四棱柱相邻两个夹角的余弦值吗？A1B1C1D1ABCD分析：二面角平面角向量的夹角回归图形EF1、设平面的法向量为(1,2,-2),平面的法向量为(-2,-4,k),

若，则k=

；若，则k=

。2、已知，且的方向向量为(2,m,1)，平面的法向量为(1,1/2,2),

则m=

.3、若的方向向量为(2,1,m),平面的法向量为(1,1/2,2),

且，则m=

.b4-5-84例1

典例讲评

例2如图，在正方体中，是的中点，点在上，且试求直线与平面所成的角的正弦值。例2正三棱柱中，D是AC的中点，当时，求二面角的余弦值。CADBC1B1A1例如图，四棱锥P-ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点,作EF⊥PB交PB于点F1求证:PA∥平面EDB;2求证:PB⊥平面EFD;2求二面角C-PB-D的大小EPDFACBy例

正三棱柱ABC-A1B1C1底面边长为a，侧棱长为，求AC1与侧面ABB1A1所成的角。ABCA1B1C1xyz利用空间向量求空间角（1）两条异面直线所成的角（2）直线与平面所成的角（3）二面角M例在底面是直角梯形的四棱锥S-ABCD中,角ABC=900,SA垂直面ABCD,SA=AB=BC=1,AD=1/2,求面SCD与面SBA所成的二面角的正切值ADCBSy练习:正方体ABCD-A1B1C1D1中,E、F分别是A1D1、A1C1的中点求:1异面直线AE与CF所成角的余弦值;2二面角C-AE-F的余弦值的大小ABCDA1B1

人人文库> 全部分类> 教育资料 > 课件下载

温馨提示

  • 1. 本站所有资源如无特殊说明，都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
  • 2. 本站的文档不包含任何第三方提供的附件图纸等，如果需要附件，请联系上传者。文件的所有权益归上传用户所有。
  • 3. 本站RAR压缩包中若带图纸，网页内容里面会有图纸预览，若没有图纸预览就没有图纸。
  • 4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
  • 5. 人人文库网仅提供信息存储空间，仅对用户上传内容的表现方式做保护处理，对用户上传分享的文档内容本身不做任何修改或编辑，并不能对任何下载内容负责。
  • 6. 下载文件中如有侵权或不适当内容，请与我们联系，我们立即纠正。
  • 7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。

最新文档

评论

0/150

提交评论