2021年人教版数学中考第一轮专题练习 相似三角形的模型(含答案)

相似三角形的模型类型1“A”字型如图，在△ABC中，AB＝AC＝8，BC＝6，点P从点B出发以1个单位长度每秒的速度向点A运动，同时点Q从点C出发以2个单位长度每秒的速度向点B运动．当以B，P，Q为顶点的三角形与△ABC相似时，求运动的时间．类型2“8”字型如图，在△ABC中，点E是线段AC上的一点，AE∶CE＝1∶2，过点C作CD∥AB交BE的延长线于点D.若△ABE的面积等于4，求△BCD的面积．类型3“母子”型(“双垂线”型是其特例)如图，已知△ABC∽△ADB，点D是AC的中点，AC＝4，求AB的长．类型4“一线三等角”型如图，在梯形ABCD中，AD∥BC，AD＝5，AB＝DC＝2.P为AD上的一点，且满足∠BPC＝∠A.(1)求证：△APB∽△DCP；(2)求AP的长．类型5“一线三直角”型已知：如图，在矩形ABCD中，E为AD的中点，BE⊥EF，求证：△ABE∽△DEF∽△EBF.

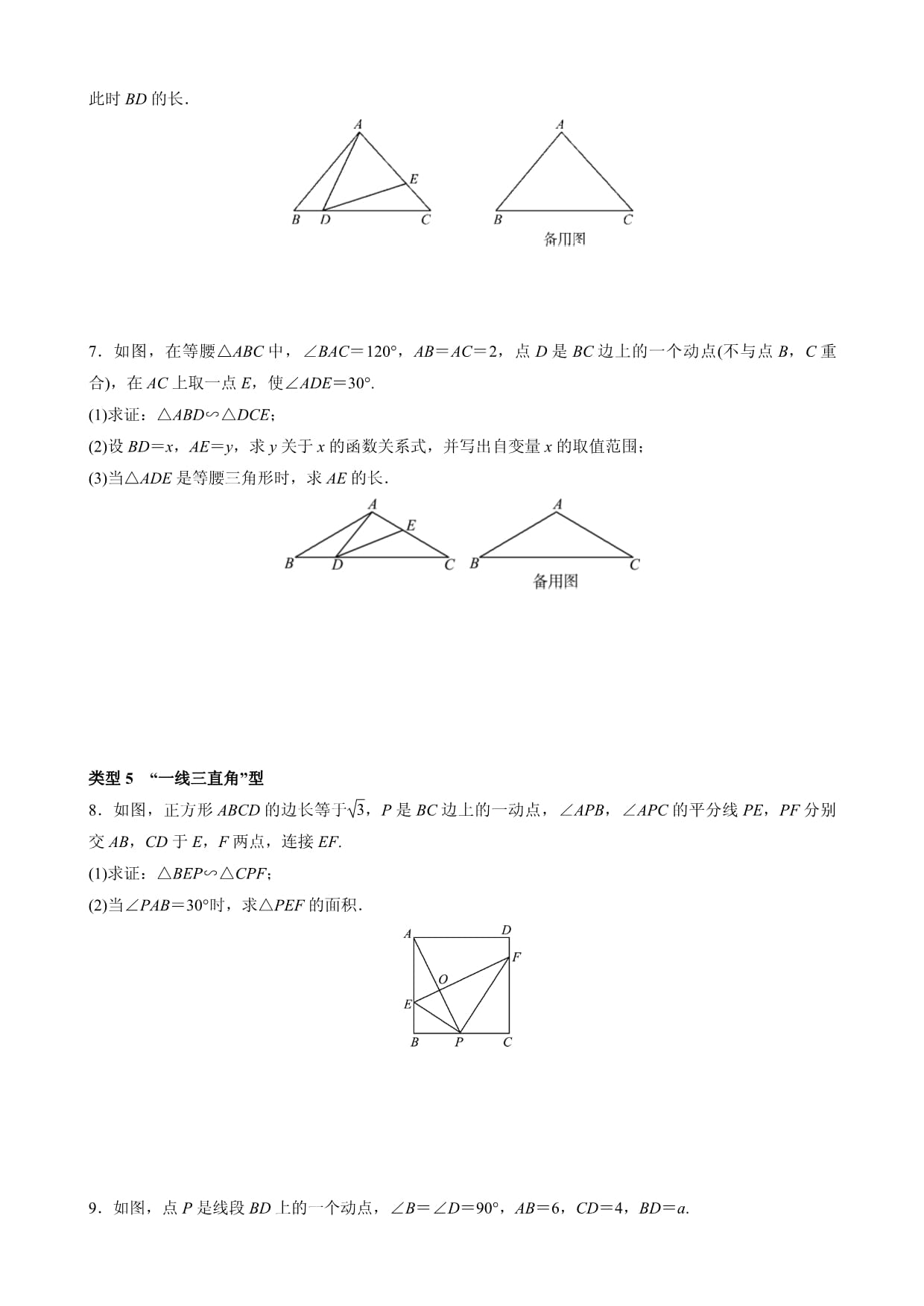
专题精炼类型1“A”字型1．如图，∠1＝∠2，要使△ABC∽△ADE，只需要添加一个条件即可，这个条件不可能是()A．∠B＝∠D B．∠C＝∠EC.eq\f(AD,AE)＝eq\f(AB,AC) D.eq\f(AC,AE)＝eq\f(BC,DE)2．如图，在△ABC中，∠C＝90°，AC＝6cm，BC＝8cm，点P从点A出发沿边AC向点C以1cm/s的速度移动，点Q从点C出发沿边CB向点B以2cm/s的速度移动，当其中一点到达终点时，另一点也随之停止运动．(1)如果点P，Q同时出发，经过几秒钟时△PCQ的面积为8cm2?(2)如果点P，Q同时出发，经过几秒钟时以P，C，Q为顶点的三角形与△ABC相似？类型2“8”字型3．如图，在▱ABCD中，点E在DC上，DE∶EC＝2∶1，连接AE交BD于点F，则△DEF与△BAF的周长之比为()A．4∶9 B．1∶3C．1∶2 D．2∶34．如图，在△ABC中，点B，D，E在一条直线上，BE交AC于点F，且eq\f(AB,AD)＝eq\f(AC,AE)，∠BAD＝∠CAE.求证：(1)△ABC∽△ADE；(2)△AEF∽△BCF.类型3“母子”型(“双垂线”型是其特例)5．已知∠PAQ＝36°，点B为射线AQ上的一固定点，按以下步骤作图：①分别以A，B为圆心，大于eq\f(1,2)AB的长为半径画弧，相交于两点M，N；②作直线MN交射线AP于点D，连接BD；③以B为圆心，BA的长为半径画弧，交射线AP于点C.根据以上作图过程及所作图形，下列结论中错误的是()A．∠CDB＝72°B．△ADB∽△ABCC．CD∶AD＝2∶1D．∠ABC＝3∠ACB类型4“一线三等角”型6．如图，在△ABC中，点D，E分别在边BC，AC上，连接AD，DE，且∠B＝∠ADE＝∠C.(1)求证：△BDA∽△CED；(2)若∠B＝45°，BC＝2，当点D在BC上运动时(点D不与B，C两点重合)，且△ADE是等腰三角形，求此时BD的长．7．如图，在等腰△ABC中，∠BAC＝120°，AB＝AC＝2，点D是BC边上的一个动点(不与点B，C重合)，在AC上取一点E，使∠ADE＝30°.(1)求证：△ABD∽△DCE；(2)设BD＝x，AE＝y，求y关于x的函数关系式，并写出自变量x的取值范围；(3)当△ADE是等腰三角形时，求AE的长．类型5“一线三直角”型8．如图，正方形ABCD的边长等于eq\r(3)，P是BC边上的一动点，∠APB，∠APC的平分线PE，PF分别交AB，CD于E，F两点，连接EF.(1)求证：△BEP∽△CPF；(2)当∠PAB＝30°时，求△PEF的面积．9．如图，点P是线段BD上的一个动点，∠B＝∠D＝90°，AB＝6，CD＝4，BD＝a.(1)当∠APC＝90°，a＝14时，求BP的长度；(2)若∠APC＝90°时，点P有两个点符合要求，即P1，P2，且P1P2＝2，求a的值；(3)若∠APC＝120°时，点P有且只有一个点符合要求，求a的值．参考答案【例1】解：设运动的时间为ts，则BP＝t，CQ＝2t，则BQ＝BC－CQ＝6－2t.∵∠ABC＝∠PBQ，∴当△BAC∽△BPQ时，eq\f(BP,AB)＝eq\f(BQ,BC)，即eq\f(t,8)＝eq\f(6－2t,6)，解得t＝eq\f(24,11)；当△BCA∽△BPQ时，eq\f(BP,BC)＝eq\f(BQ,AB)，即eq\f(t,6)＝eq\f(6－2t,8)，解得t＝eq\f(9,5).综上所述，当以B，P，Q为顶点的三角形与△ABC相似时，运动的时间为eq\f(24,11)s或eq\f(9,5)s.【例2】解：∵CD∥AB，∴△ABE∽△CDE.又∵AE∶CE＝1∶2，∴eq\f(S△ABE,S△CDE)＝(eq\f(AE,CE))2＝(eq\f(1,2))2＝eq\f(1,4).又∵S△ABE＝4，∴S△CDE＝16.∵AE∶CE＝1∶2，∴CE＝2AE，∴S△BCE＝2S△ABE＝2×4＝8，∴S△BCD＝S△CDE＋S△BCE＝16＋8＝24.【例3】解：∵AC＝4，D是AC的中点，∴AD＝DC＝2.∵△ABC∽△ADB，∴eq\f(AB,AD)＝eq\f(AC,AB)，即eq\f(AB,2)＝eq\f(4,AB)，解得AB＝2eq\r(2).【例4】(1)证明：∵AD∥BC，AB＝DC，∴∠A＝∠D.又∵∠ABP＝180°－∠A－∠APB，∠DPC＝180°－∠BPC－∠APB，∠A＝∠BPC，∴∠ABP＝∠DPC，∴△APB∽△DCP.(2)解：∵△APB∽△DCP，∴eq\f(AP,CD)＝eq\f(AB,DP)，即eq\f(AP,2)＝eq\f(2,5－AP)，解得AP＝1或AP＝4.【例5】证明：∵BE⊥EF，∴∠AEB＋∠DEF＝90°.∵∠AEB＋∠ABE＝90°，∴∠ABE＝∠DEF.又∵∠A＝∠D＝90°，∴△ABE∽△DEF，∴eq\f(AB,DE)＝eq\f(BE,EF).∵E为AD中点，∴DE＝AE，∴eq\f(AB,AE)＝eq\f(BE,EF).∵∠A＝∠BEF＝90°，∴△ABE∽△EBF，∴△ABE∽△DEF∽△EBF.1．D2．解：(1)设经过xs时△PCQ的面积为8cm2，则PC＝(6－x)cm，CQ＝2xcm，则eq\f(1,2)(6－x)·2x＝8，整理，得x2－6x＋8＝0，解得x1＝2，x2＝4.∴如果点P，Q同时出发，经过2s或4s时△PCQ的面积为8cm2.(2)设经过ts时以P，C，Q为顶点的三角形与△ABC相似，则PC＝(6－t)cm，QC＝2t(cm)．当△PCQ∽△ACB时，eq\f(PC,AC)＝eq\f(QC,BC)，即eq\f(6－t,6)＝eq\f(2t,8)，解得t＝eq\f(12,5)；当△PCQ∽△BCA时，eq\f(PC,BC)＝eq\f(QC,AC)，即eq\f(6－t,8)＝eq\f(2t,6)，解得t＝eq\f(18,11).综上所述，如果点P，Q同时出发，经过eq\f(12,5)s或eq\f(18,11)s时，以P，C，Q为顶点的三角形与△ABC相似．3．D4．证明：(1)∵∠BAD＝∠CAE，∴∠BAD＋∠CAD＝∠CAE＋∠CAD，即∠BAC＝∠DAE.在△ABC和△ADE中，∵eq\f(AB,AD)＝eq\f(AC,AE)，∠BAC＝∠DAE，∴△ABC∽△ADE.(2)∵△ABC∽△ADE，∴∠C＝∠E.在△AEF和△BCF中，∵∠C＝∠E，∠AFE＝∠BFC，∴△AEF∽△BCF.5．C6．(1)证明：∵∠B＝∠ADE＝∠C，∠BAD＝180°－∠ADB－∠B，∠CDE＝180°－∠ADB－∠ADE，∴∠BAD＝∠CDE，∴△BDA∽△CED.(2)解：当AD＝AE时，∠ADE＝∠AED＝45°，∴∠ADE＝∠B，∴点D与点B重合，不合题意，舍去；当EA＝ED时，如图①，则∠EAD＝∠1＝45°，∴AD平分∠BAC，∴AD垂直平分BC，∴BD＝1.当DA＝DE时，如图②，∵∠1＝∠C，∠DAE＝∠CAD，∴△ADE∽△ACD，∴eq\f(AD,AC)＝eq\f(DE,CD)，∴DC＝CA＝eq\f(\r(2),2)BC＝eq\r(2)，∴BD＝BC－DC＝2－eq\r(2).综上所述，当△ADE是等腰三角形时，BD的长为1或2－eq\r(2).7．(1)证明：∵在等腰△ABC中，∠BAC＝120°，∴∠B＝∠C＝30°，∴∠B＝∠ADE.∵∠ADC＝∠ADE＋∠EDC＝∠B＋∠DAB，∴∠EDC＝∠DAB，∴△ABD∽△DCE.(2)解：∵AB＝AC＝2，∠BAC＝120°，∴BC＝2eq\r(3)，∴DC＝2eq\r(3)－x，EC＝2－y.∵△ABD∽△DCE，∴eq\f(AB,BD)＝eq\f(DC,CE)，即eq\f(2,x)＝eq\f(2\r(3)－x,2－y)，化简得y＝eq\f(1,2)x2－eq\r(3)x＋2(0<x<2eq\r(3))．(3)解：设BD＝x，AE＝y，①当AD＝DE时，由(1)可知此时△ABD≌△DCE，则AB＝CD，即2＝2eq\r(3)－x，解得x＝2eq\r(3)－2，代入y＝eq\f(1,2)x2－eq\r(3)x＋2，得y＝4－2eq\r(3)，即AE＝4－2eq\r(3)；②当AE＝ED时，∠EAD＝∠EDA＝30°，∴∠AED＝120°，∴∠DEC＝60°，∴∠EDC＝90°，∴ED＝eq\f(1,2)EC，即y＝eq\f(1,2)(2－y)，解得y＝eq\f(2,3)，即AE＝eq\f(2,3)；③当AD＝AE时，∠AED＝∠ADE＝30°，∴∠EAD＝120°，此时点D与点B重合，与题目不符，此情况不存在．综上所述，当△ADE是等腰三角形时，AE＝4－2eq\r(3)或eq\f(2,3).8．(1)证明：∵PE平分∠APB，PF平分∠APC，∴∠APE＝eq\f(1,2)∠APB，∠APF＝eq\f(1,2)∠APC，∴∠APE＋∠APF＝eq\f(1,2)(∠APB＋∠APC)＝90°，∴∠EPF＝90°，∴∠EPB＋∠BEP＝∠EPB＋∠FPC＝90°，∴∠BEP＝∠FPC.又∵∠B＝∠C＝90°，∴△BEP∽△CPF.(2)解：∵∠PAB＝30°，∴∠BPA＝60°，∴∠BPE＝30°.在Rt△ABP中，∵∠PAB＝30°，AB＝eq\r(3)，∴BP＝1.在Rt△BPE中，∴∠BPE＝30°，BP＝1，∴EP＝eq\f(2\r(3),3).在Rt△CPF中，∵CP＝eq\r(3)－1，∠FPC＝60°，∴PF＝2CP＝2eq\r(3)－2，∴S△PEF＝eq\f(1,2)PE·PF＝eq\f(1,2)×eq\f(2\r(3),3)×(2eq\r(3)－2)＝2－eq\f(2\r(3),3).9．解：(1)∵∠B＝∠D＝90°，∠APC＝90°，∴∠A＋∠APB＝∠CPD＋∠APB＝90°，∴∠A＝∠CPD，∴△ABP∽△PDC，∴eq\f(BP,CD)＝eq\f(AB,PD)，即eq\f(BP,4)＝eq\f(6,14－BP)，解得BP＝2或12.(2)设BP＝x，则PD＝a－x.由(1)可知△ABP∽△PDC，∴eq\f(AB,PD)＝eq\f(BP,DC)，即eq\f(6,a－x)＝eq\f(x,4)，∴x2－ax＋24＝0.设方程的两个根为x1，x2，根据根与系数的关系可知x1＋x2＝a，x1x2＝24，∵P1P2＝2，∴|x1－x2|＝2，∴(x1－x2)2＝(x1＋x2)2－4x1x2＝4，∴a2－4×24＝4，解得a1＝10，a2＝－10(舍去)，∴a＝10.(3)如图，作∠AEP＝∠CFP＝120°，则∠AEB＝∠CFD＝60°.∵AB＝6，CD＝4，∴BE＝eq\f(\r(3),3)AB＝2eq\r(3)，DF＝eq\f(\r(3),3)CD＝eq\f(4\r(3),3)，∴AE＝2BE＝4eq\r(3)，CF＝2DF＝eq\f(8\r(3),3).∵∠AEP＝∠CFP＝∠APC＝120°，∠APF＝∠AEP＋∠EAP＝∠APC＋∠CPF，∴∠EAP＝∠CPF，∴△EPA∽△FCP，∴eq\