线面垂直面面垂直的性质定理

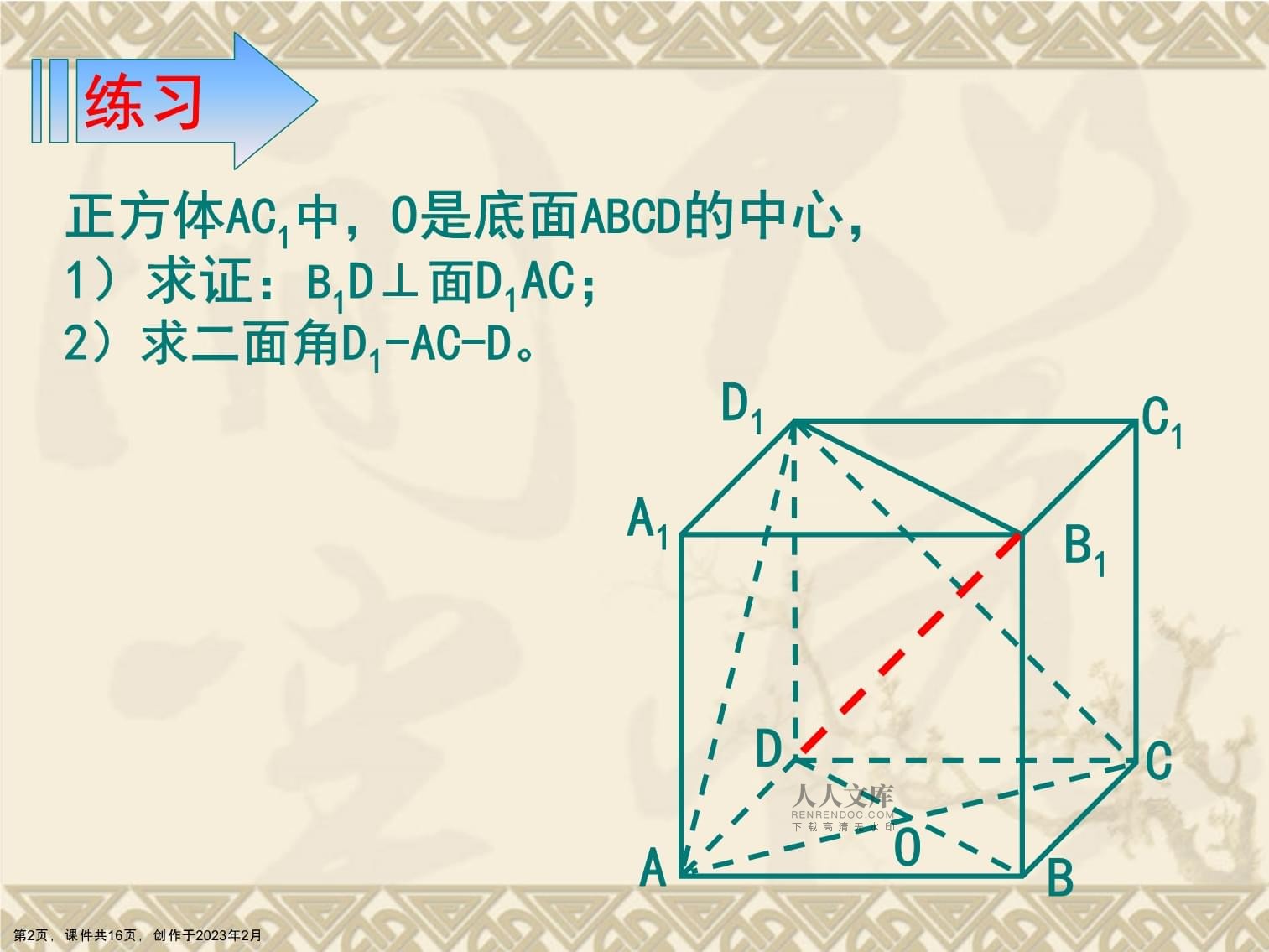
关于线面垂直面面垂直的性质定理第1页，课件共16页，创作于2023年2月练习正方体AC1中，O是底面ABCD的中心，1）求证：B1D⊥面D1AC；2）求二面角D1-AC-D。BCADD1C1B1A1O第2页，课件共16页，创作于2023年2月如果直线l与平面内的任意一条直线都垂直，我们说直线l与平面互相垂直。直线与平面垂直定义：线面垂直则线线垂直.一条直线与一个平面内的两条相交线都垂直，则该直线与此平面垂直．直线与平面垂直判定定理：线线垂直则线面垂直.温故知新第3页，课件共16页，创作于2023年2月探究ABCD第4页，课件共16页，创作于2023年2月探究αab第5页，课件共16页，创作于2023年2月线面垂直的性质定理：垂直于同一个平面的两条直线平行αabo证明：假设a与b不平行.∴b’⊥α.∴过点o的两条直线b和b’都垂直平面α，这是不可能的，b’1.已知:a⊥α,b⊥α求证:a//b记直线b和α的交点为o,则可过o作b’∥a∵a⊥α,∴a∥b.反证法符号语言：

线面垂直线线平行简述：第6页，课件共16页，创作于2023年2月找二面角的平面角说明该平面角是直角。面面垂直的判定方法：1、定义法：2、判定定理：（线面垂直面面垂直）温故知新要证两平面垂直，只要在其中一个平面内找到另一个平面的一条垂线。第7页，课件共16页，创作于2023年2月知识探究：思考1:如果平面α与平面β互相垂直，直线l在平面α内，那么直线l与平面β的位置关系有哪几种可能？αβllαβlαβ平行相交线在面内第8页，课件共16页，创作于2023年2月知识探究：

思考2:黑板所在平面与地面所在平面垂直，在黑板上是否存在直线与地面垂直？若存在，怎样画线？αβ第9页，课件共16页，创作于2023年2月

两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直。面面垂直线面垂直αβaAl平面与平面垂直的性质定理：符号语言：作用：何时用:已知面面垂直时.关键:在一个平面内作(找)出垂直于交线的直线.第10页，课件共16页，创作于2023年2月AA 推论:两个平面垂直,过其中一个平面内一点作另一个平面的垂线,这条垂线在这个平面内.αβαβPP第11页，课件共16页，创作于2023年2月例1：如图，AB是⊙O的直径，C是圆周上不同于A，B的任意一点，平面PAC⊥平面ABC，BOPAC(2)判断平面PBC与平面PAC的位置关系。(1)判断BC与平面PAC的位置关系，并证明。(1)证明：∵AB是⊙O的直径，C是圆周上不同于A，B的任意一点∴∠ACB=90°∴BC⊥AC又∵平面PAC⊥平面ABC，平面PAC∩平面ABC＝AC,BC

平面ABC∴BC⊥平面PAC(2)又∵BC平面PBC，∴平面PBC⊥平面PAC第12页，课件共16页，创作于2023年2月例2：如图，已知PA⊥平面ABC，平面PAB⊥平面PBC，求证：BC⊥平面PABPABCE证明：过点A作AE⊥PB，垂足为E，∵平面PAB⊥平面PBC，平面PAB∩平面PBC=PB，∴AE⊥平面PBC∵BC平面PBC∴AE⊥BC∵PA⊥平面ABC，BC平面ABC∴PA⊥BC∵PA∩AE=A，∴BC⊥平面PAB第13页，课件共16页，创作于2023年2月例3证明：设bαβal在α内作直线b⊥l面面垂直性质线面垂直性质第14页，课件共16页，创作于2023年2月2、会利用“转化思想”解决垂直问题线面关系线线关系面面关系线面平行线线平行线面垂直线线垂直面面垂直