信与线性系统分析习题答案吴大正第四版高等教育出版社

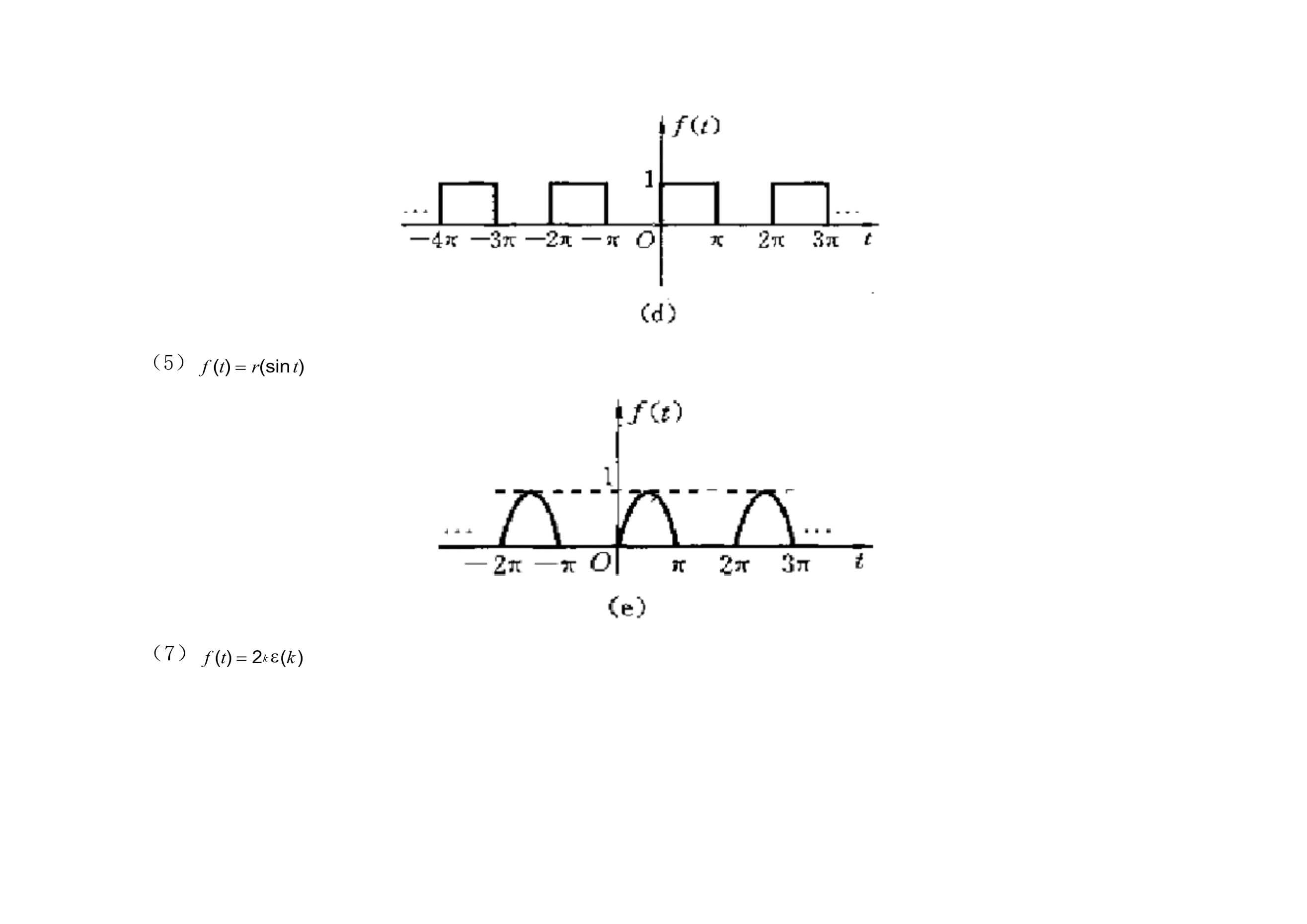
。（2）（4）

fet,tf(sin

（3）（5）

ff（7）

f2k(k

（10）

f(k)(1)k(k)解：（2）

f(t)et,t（3）f(t)(t)（4）f(t)(sint)（5）

f（7）f2k(k)（10）

f(k)1()k(k)

]。（1）

f

(t(t(t2)

（2）

f

r(t)

2r(t

r(t2)（5）

f

r(2t)(2

（8）

f(k)

(k)

(k

)]（11）

f(k)

6

(k)(k

7)]

（12）

f(k)

2k(3

k)(k（2）f（2）fr(t)2r(tr(t2)

f

(t2)（5）

f

r(2t)(2（8）

f(k)

)]（11）

f

k)sin(k6

)(k

7)]（12）

f(k

)2k

(3

)(k1-31-4。如果，确定其。（2）

f(k)2

cos(4

k )cos( 4 3

6

（5）

f 5

3cost

2sin(t)解：

f(t1-5。（1）

f(t

1(t)

（2）

f

1

1

（5）

f

2t)

（6）

f

.5

2)df(t)

t f

(x（7） dt 8）解：为（1）

f(t

1(t)（2）

f

1

1)（5）

f

2t)（6）

f(0

.5t2)df(t)（7） dtt（8）

f(

)dx

f(k

1-7。（1）

f

2)(k)

（2）

f

2)（3）

f

)(

)(k

)

（4）

f(k

2)（5）

f(k

(k

（6）

f(k)

f

3)解：1-11

df(t)。dt解：由1-11

f3

1-12(a)

f3

f3

2

展宽为原来两倍而得

f3

f(t3

1-12(b)

f(t3

右3

1-12(c)1-12(d)。dtd（1）

d2dt2

(t)

（2）

t)

[et(t)]dt（5）

t

42)dt

（8）

t 1

x'(x

)dx1-13Cu (t)Ci (t)L 1-201-181-23x(0)

f

()yy（1）

y(t)

etx(0)

tnx0

(x)dx

（2）

y(t)

ft)x(0)0

f(x)dx（3）

y(t)

in[x(0t]0

f(x)dx

（4）

y(k

(0.5)k

x(0)

f(k)f(k

2)（5）

y(k)

kx()kj0

f(j)1-25稳定？

f

y 、时不变、因果、zs（1）

y (t)zs

df(t)dt

（2）

y (t)zs

f(t)

（3）

y (t)zs

f(t)（4）

y (t)zs

f(t)

（5）

y (k)zs

f(k)f(k

（6）

y (kzs

(k

2)

(k)7）

y (k)zs

kj0

f(j)

（8）

y (k)zs

fk)1-28LTIx(0)。已知当激励y

(k(k时全响应为1若不变当激励

f(k时全响应

(k)(0)2

(k)若2x(0当激励4f(k时求全响应。二章（1）y''(t)

y'(t)

y(t)

f

y(0)1,y'(0 )1（4）y''(t)

y(t)

f

y(0)2,y'

)00

y

) y'(0 )。 。（2）y''(t)（4）y''(t)解：

y'(t)y'(t)

y(t)y(t)

f''(t),f'(t),

yy(0

)1,y')1,y'(0

)1)2,

f(t)(t)f(t)e2t(t)2-4、全。（2）

y''(t)

y'(t)

y(t)

f'(t)

f

y

)1,y'(

)2

f(t)

et(t)2-82-4St)uR(t)2-122-6uC(t2-162-82-8(b)、(c)、(d)均为单位冲激试求下列卷积并画出。（1）

f(t)*1

f (t)2

（2）

f(t)*1

f (t)3

（3）

f(t)1

f (t)4（4）

f(t)*1

f (t)2

f (t)2

（5）

ft)*2f t)1 4

f 3

3)2-9(a)2-9(b)2-9(c)所示。2-9(d)2-9(e)2-20

f(t)1

t(t)

f (t)2

(t)(t

2

(t)

f(t)1

f 2

1)

'(t

2)2-22LTI

f(t)

y(t)

y(t)

t

e2(tx

f(x

2)dxh(t)2-19

f(t)

(t)

2-20h a

(t1

h b

(t3)0，

k3.1、试求序列

fk=1

的差分f(k、f和f(i。i=-3.6、求下列差分方程所描述的LTI离散系统的零输入相应、零状态响应和全响应。1）y(k)-2y

)

f(k

f(k)2(ky

-13）y(k

)

y

)

f(k

f

)

4)(k

y

-115 ）1y(k)2y

)y

-2)

f(k

f(k)3( )k(ky)3,y)2、求下列差分方程所描述的离散系统的单位序列响应。2）y(k)-y(k

-2)

f(k)5）y(k)-

y

)8y(k

-2)

f(k)、求图所示各系统的单位序列响应。（a）（c）、求图所示系统的单位序列响应。、各序列的图形如图所示，求下列卷积和。（1）f

(k)

(k)（2）

(k)

(k)（3）

(k)

(k)（4）f

(k

(k

(k)1 2 2 3 3 4 2 1 33.9、求图所示系统的单位序列响应和阶跃响应。、若LTIg(k

0

kk，求其单位序列响应。、如图所示系统，试求当激励分别为

f(k)(k

（2）

f(k)05

(k)时的零状态响应。3.18h

=2cosk

k=ak

k=k-ak-1，1 4 2求该系统的零状态响应

y (k（）zs3.22、如图所示的复合系统有三个子系统组成，它们的单位序列响应分别为h1

k=

k，h2

k=

k-5，求复合系统的单位序列响应。Ω和T。（1）

e

（2）

cos[2

(t3)]（3）（4）（5）

cos(2

4

（6）

cos(2

cos(3

cos( 54-15。4-154.104-184-184-111Ω电阻两端的电压u(t4-19求u(t的三角形式傅里叶系数。利用（1）的结果和u12

)

，求下列无穷级数之和S11113 5 1Ω电阻上的平均功率和电压有效值。

......利用（3）的结果求下列无穷级数之和S11 132 52

1 ......724-194.17下列函数的（1）

f(t)

sin[2(t2)](t2) 2

t（2）

f(t)2

t

,t2（3）

f(t)

,t下列信号的傅里叶变换（1）

f(t)e(t

（2）

e3(t1)'(t（3）（5）

f(t2

（4）

e2t(t4-234-23F[)]F()下列函数的频谱：（1）

（3）tdf(t)dt

（5）(1-f-（8）e

f(3-

（9）df(t)*1dt 下列函数的傅里叶变换（1）

1,00F(j)0（3）F(j)25）Fj)2n0

e-j(2n1)4.234-25。

fg2

(t2、(t2卷之4-254.254-27。（b）中冲激1。4-274-29

()F()下列各值[不必出F()]1F(0)

F()|0

2

F(d3

F()2d4-29。

f2t)dt

1

F(j)2d（1）

[sin(t)

2]dt

（） dx t

(1

x2)2一周期为T

f(t)，已知其指数形式的傅里叶系数为F，求下列周期信号的傅里叶系数n（1）

f1

f(tt0

（2）

f(t)2

f(t)（3）

f3

dfdt

（4）

f(t)4

f(at),a04.314-30u

(t)

(tHj)U2j)

R、R1 2

2 S值。

I(j)S4-30LTI

f(t

y(t)

1a

s(

a)f(xa

2)dxas() S(j)H(j)。LTIH(j)22

jj

f(t)cos(2t)y(t。一理想低通滤波器H(jH(j),/s3

3rad/sLTI ej2,6rad/s0H(j)ej,06rad/s 2 0,

f(t)

y(t。t4-35y(t)

f2(t)

f(t。该线性吗？

f(t)

t

y(t频谱或画频谱。

f

1y(t频谱或画频谱。24.454-42(a)(b)(4.454-42(a)sin(2t)y(t)。

f(t)

,s(t)图4-424.48

f)100Hzf。s（1）

f(3

（2）

f2(t)（3）

f

f(2

f

f2(t)4.50

f(t52ttf

(tf s

f。1

1 1 1 s T1

f(t)及

ft)在率区间-2kHz2kHzs2若将

f(t输入到截止fs

幅度为理想低通滤波器即率响应,f 500HzH(j)H()s0,f画出滤波器输出谱并出输出y(t。

500Hz图4-47图4-484-494.53。（2）

f(k)(2

)k(0

3)(N

4)5-25-15-3

(t)

eat(t)

sin(t)(t)，，，

cos(t)(t)，

f(t)

F(s)。（1）

et(t)

e(t2)

（3）

(t)

(t

1)]（5）

（7）

sin(2t

(t)4（9）

tint)d0

（11）

d2dt

(t)]t2e2t(t)（13）

te(t3)（15）

1)1231235-4t

f(t)

F(s)s2

1s

y(t)

Y(s)。（1）

et

f( 2

tf（4）

(2

1)5-6

F(s

f

)

f(。F(s)

2s

F(s)

3s1（1）

(s1)2

（2）

s(s1)5-2

0tt

f(t)

F(s)。5-2

F(s)

f(t)。1 s

4s

2s4（1）

(s

2

4

（3）s2

3s

（5）

s(s2 4)1 s5（7）

s(s

1)2

（9）

s(s2

2

5)

F(s)

f。1eTs

e2(s3)

e2s)（1）

s

（3）

s

（6）

s2 2其如所示：下图所示：下图所示：F(s)

f

t05-10

是T0

t

1

f o 。1（1）1

e

（2）

e2s)

y''(t)

y'(t)

y(t)

f(t)。

f(t)

y(

)1,

'(0

)2。

f(t)

et(t),

y

)

,y'

)1。

y(t)1

(ty'(t) 1

y(t)1

y (t)2

f(t)y'2

(t)

y(t)1

y (t)2

f(t)1

f(t)

y(0 )1

y (0 )2

y

(t)

y2

(t。5-15LTI

y''(t)

y'(t)

y(t)

f'(t)

f(t)下列条件下零输入响应和零状态响应。（1）

f(t)

(t),

y(

)

,y'(

)1。。（2）

f(t)

e2

t(t

y(

)1,

'(0

)1。。5-16LTI

y''(t)

y'(t)

y(t)

f'(t)

f(t)。（1）

f(t)

y(

)1,

'(0

)3。（2）

f(t)

e2t

y

)1,

'(0

)2。。LTI

h(t)

g(t)。（1）

y''(t)

y'(t)

y(t)

f'(t)

f(t)已知函数初始状态如，零输入

y (t)。H(s)

s

y(0)

y'(0

)1（1） s2 5s6， H(s)

s

y(0)y'(0 )y''(0

)1（3）

s(s2

3

2)， 5-225-54H (s)1

1s

H (s)2

1s

h(t)3

h4

(t)

e2

h(t)。5-265-7a、b、c。

f(t)

(t)

y (t)zs

5e2

5e3t(t)，LTI。已知当激励

f(t)1

(t)

时其全响应y (t)1

(t)

et(t)

；当激励

f (t)2

(t时

y (t)2

3et(t。（1）若

f (t)3

e2t(t)

求的全响应。(t) u5-8

(t5-42H

j)

11

jj

f(t)

y (t)。（1）

f(t)

(t)

（2）

f(t)

t(t)5-502

e[s]

2 ,3

e[s]1（1）

(ss

（2）

(ss4 ,e[s]

s4

,1

e[s]0（3）s24

（4）

(s2

s6.4。（1）F1z,z2）F()3 ,z（3）F(z)

1 0,z（4）F(z),z1 ,z11 ,z1a11 ,z1a1 ,z1a1

z

20aa

z5(k)1ak(k)

zz

(k)

z(z

zz。（1）1(1)k(k2

3）()k(k)（5）k

(k

（7）k[(k)(k4)]（9）(1)kcos(k(k)2 28zF()mk

f(k)。（1）F(z)

z21

（3）F(z) z2(z1)(z1)

(zz2)2 3z。（1）F（2）F（3）F

2(z12(z121

1)(z132)(z133

,z1) 3,z1) 2,z12(z2

)2(z1)（4）F

(z12

3 1,)2(z1) 3

z12z。（1）F(z)

12

,z1（2）F(z)

2

,z1（5）F(z)

(z1(z(z1(

z1)1),z1（6）F(z)

2az,za(za)36.13

f(k)

F()z1）ki0

aif

）akki0

f(i)6.15z。（）y(k)0

y(k1)0,y(1)1（3）y(k2)

y(k1)

y(k)0,y(0)0,y1)36.17LTIy(k)

y(k1)

y(k2)

f(k)y(1)1,y(2)14

,f(k)(ky

(k)yzs

(ky(k。6-2LTIh(kg(k。6-2。（1）

f(k)

k(k

f(k)

(13

k(k)6-5。求该的单位序列响应h(k。

f(k)

(12

k(kyzs

(k。6-6H(z)；h(k；6.26LTI

f(k)

(1)k2

(k1

1y (k)2( )2

)k(k)3H(z6-29LTIy(1)

f(k)(ky1

(k)2(ky(1)1f2

(k)12

k(k)y2

(k)

1(k)。求

f(k)(2

)k(k的零。6.316-1032h2

(k(1k(k3H3

(k)

zz

f(k)(ky1

(k3(k1(k。求1h1

(k。LTI为g(kf(k时，其零状态

f(k)。

y (k)kzki0

g(i)

f(k)满足方程

f(k)(k)ki0

f(i)

f(k) 。6.37

f(k与其3输入（4）进行。求该系统频率响应。6-

f(k)y(k)。列该的差分方程。问该存在频率响应否？什么？

f(k)

20cos(2

k30.8时yss

(k。7.37-5RC

U、极点。H(s)

22U1aH(s)2且已知当s求出H(s表达式。

H()1。

Hj表达式。07Z(s)U1(s)21j

3Z(0)

RLC值。I(s) 21472ab。7-29。（1）a0

2,a1

3；（2）a0

2,a1

3；（3）a0

2,a1

3。7-30。（1）a0

1,a2

1；（2）a0

1,a2

1；（3）a0

1,a2

1。7-31)2

s4

KKy(k)1.5

y(k1)y(k2)

f(k1)算输入

f(k)(0.5)k(k)yzs

(k)。7.287-36函数H(s。00H()。(a)s7-41(a)。中有一个回路。其增益为(b)s7-41(b)。中有一个回路。其增益为7.32。（1）

s1

s2