港澳台联考数学课件-空间直线的方程

空间直线的方程2021/5/71分析：

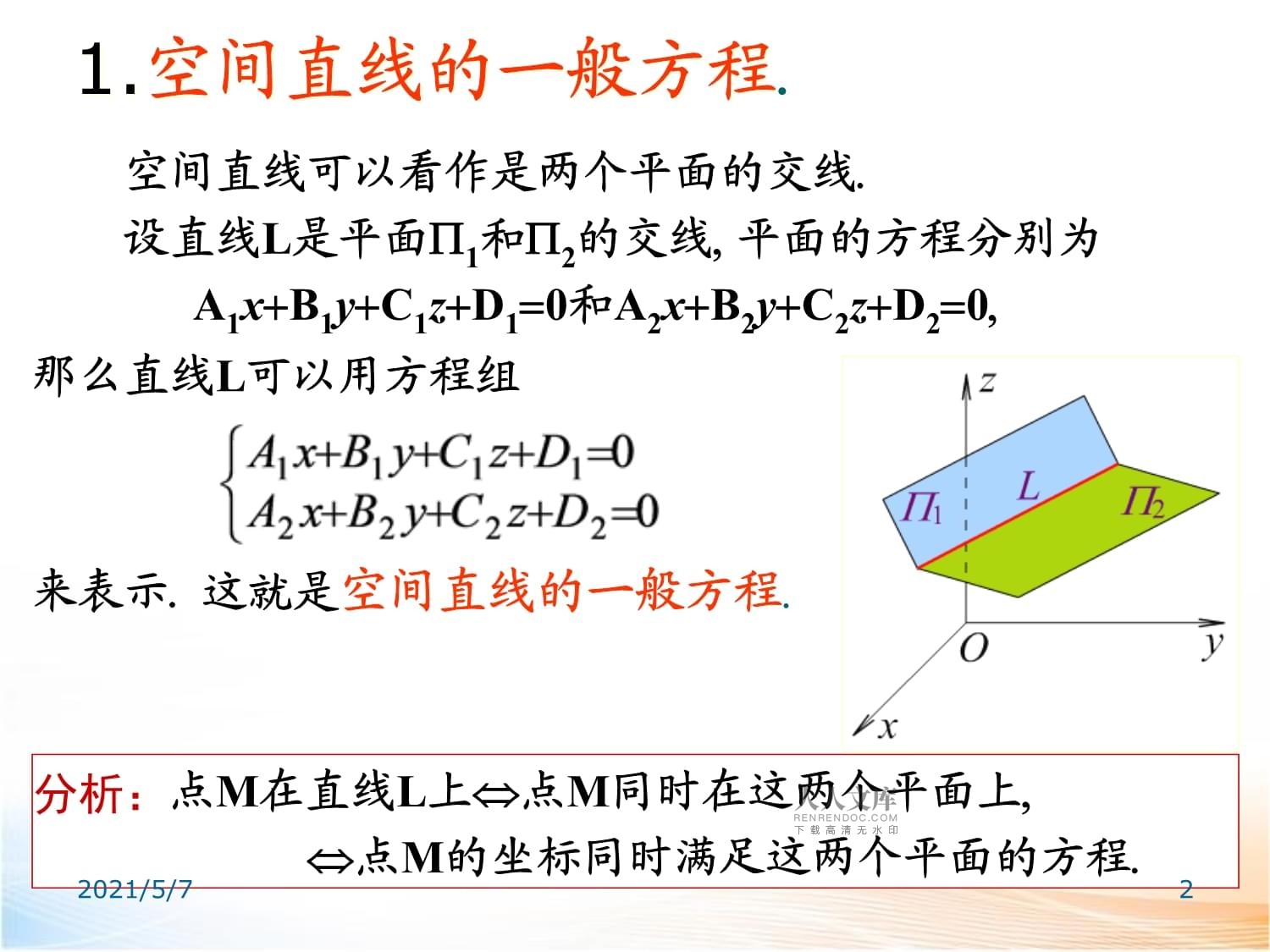
点M在直线L上点M同时在这两个平面上,

点M的坐标同时满足这两个平面的方程.1.空间直线的一般方程.

空间直线可以看作是两个平面的交线.

设直线L是平面1和2的交线,

平面的方程分别为

A1x+B1y+C1z+D1=0和A2x+B2y+C2z+D2=0,这就是空间直线的一般方程.来表示.

那么直线L可以用方程组2021/5/72例1

联立方程表示平行于yoz坐标面的平面表示平行于xoz坐标面的平面的解是(3,4,z),其图形是平面x-3=0与y-4=0的交线，它平行于z轴.xyzo342021/5/73代表平面y=5x+1与平面y=x-3的交线.

例2联立方程

2021/5/74

如果一个非零向量平行于一条已知直线,这个向量就叫做这条直线的方向向量.方向向量

直线上任一向量都平行于该直线的方向向量.

当直线L上一点M0(x0,y0,z0)和它的一方向向量s=(m,n,p)为已知时,直线L的位置就完全确定了.确定直线的条件

若已知一条直线的一般方程则此直线的方向向量为2021/5/75例3

求通过点M0(x0,y0,z0),方向向量为s=(m,n,p)的直线的(x-x0,y-y0,z-z0)//s,

从而有这就是直线的方程,叫做直线的对称式方程或标准方程.

直线的任一方向向量s的坐标m、n、p叫做这直线的一组方向数.向量s的方向余弦叫做该直线的方向余弦.则从M0到M的向量平行于方向向量:

设M(x,y,z)为直线上的任一点,方程.2021/5/76通过点M0(x0,y0,x0),方向向量为s=(m,n,p)的直线方程:说明:

某些分母为零时,其分子也理解为零.直线方程为例如,当直线方程为2021/5/77通过点M0(x0,y0,z0),方向向量为s=(m,n,p)的直线方程:此方程组就是直线的参数方程.2021/5/78提示：

先求直线上的一点,再求这直线的方向向量s.

提示：提示：提示：于是(1,-2,0)是直线上的一点.

在直线的一般方程中令x=1,

解

以平面x+y+z=-1和2x-y+3z=4的法线向量的向量积作为直线的方向向量s:4i-j-3k.s(i+j+k)(2i-j+3k)

可得y=-2,z=0.

所给直线的对称式方程为

例4

所给直线的参数方程为x14ty2tz3t

2021/5/79练习：

将一般方程解先在直线上找一点.再求直线的方向向量令x=1,解方程组,得已知直线的两平面的法向量为是直线上一点.化成标准方程及参数方程.2021/5/7109、人的价值，在招收诱惑的一瞬间被决定。2023/2/32023/2/3Friday,February3,202310、低头要有勇气，抬头要有低气。2023/2/32023/2/32023/2/32/3/20234:31:43PM11、人总是珍惜为得到。2023/2/32023/2/32023/2/3Feb-2303-Feb-2312、人乱于心，不宽余请。2023/2/32023/2/32023/2/3Friday,February3,202313、生气是拿别人做错的事来惩罚自己。2023/2/32023/2/32023/2/32023/2/32/3/202314、抱最大的希望，作最大的努力。03二月20232023/2/32023/2/32023/2/315、一个人炫耀什么，说明他内心缺少什么。。二月232023/2/32023/2/32023/2/32/3/202316、业余生活要有意义，不要越轨。2023/2/32023/2/303February202317、一个人即使已登上顶峰，也仍要自强不息。2023/2/32023/2/32023/2/32023/2/32021/5/711故所给直线的标准方程为参数式方程为解题思路:先找直线上一点;再找直线的方向向量.2021/5/712例5求点P到直线L的距离及P在L上的投影Q.解2021/5/713两直线的夹角

两直线的方向向量的夹角(通常指锐角)叫做两直线的夹角.

设直线L1和L2的方向向量分别为

s1=(m1,n1,p1)和s2=(m2,n2,p2),那么L1和L2的夹角j满足2021/5/714两直线垂直与平行的条件

设有两直线L1L2m1m2+n1n2+p1p2=0;

则方向向量分别为(m1,n1,p1)和(m2,n2,p2)的直线的夹角余弦:2021/5/715提示：直线与平面的夹角

当直线与平面不垂直时,直线和它在平面上的投影直线的夹角j称为直线与平面的夹角,当直线与平面垂直时,规定直线与平面的夹角为90.

设直线的方向向量为s=(m,n,p),平面的法线向量为n=(A,B,C),则直线与平面的夹角j

满足

2021/5/716

方向向量为(m,n,p)的直线与法线向量为(A,B,C)的平面的夹角j

满足

直线与平面垂直和平行的条件

设直线L的方向向量为s=(m,n,p),平面P的法线向量为n=(A,B,C),则

L//PAm+Bn+Cp=0.2021/5/717

上述方程表示通过定直线L的所有平面的全体,称为平面束.平面束

考虑三元一次方程:A1x+B1y+C1z+D1+l(A2x+B2y+C2z+D2)=0,即(A1+lA2)x+(B1+lB2)y+(C1+lC1)z+D1+lD2=0,其中l为任意常数.其中系数A1、B1、C1与A2、B2、C2不成比例.

设直线L的一般方程为2021/5/718补例.

求直线在平面上的投影直线方程.解过已知直线的平面束方程从中选择