《正弦定理》(精选)北师大版1课件

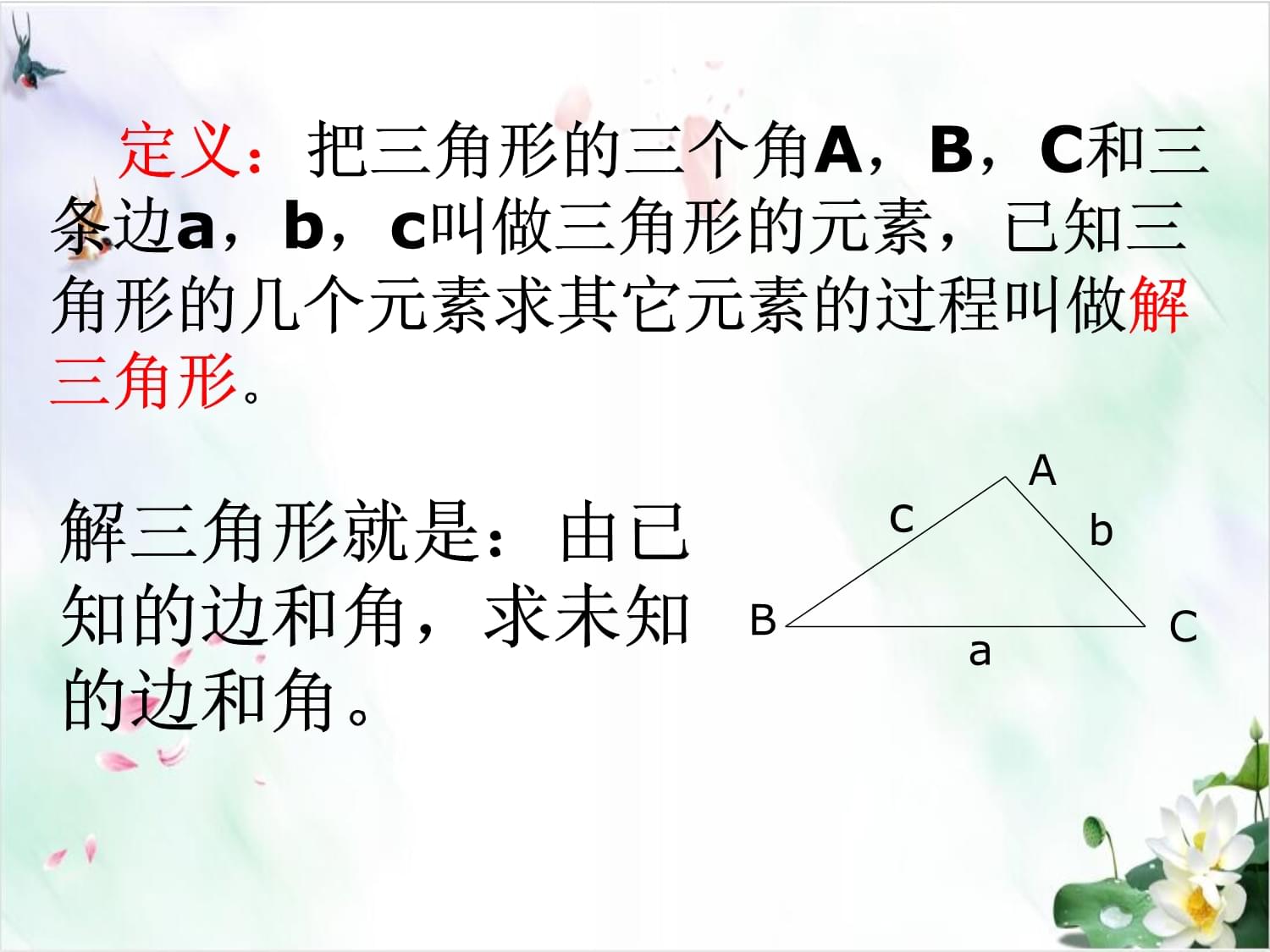
1、正弦定理正弦定理解三角形解三角形 定义：ABCabc解三角形就是： 定义：ABCabc解三角形就是： 定义：把三角形的三个角A，B，C和三条边a，b，c叫做三角形的元素，已知三角形的几个元素求其它元素的过程叫做解三角形。ABCabc解三角形就是：由已知的边和角，求未知的边和角。正弦定理ppt(精选)北师大版1正弦定理ppt(精选)北师大版1 定义：把三角形的三个角A，B，C和三条边a，b，c叫做正弦定理正弦定理ppt(精选)北师大版1正弦定理ppt(精选)北师大版1正弦定理正弦定理ppt(精选)北师大版1正弦定理pp正弦定理：在一个三角形中，各边和它所对角 的正弦的比相等,即正弦定理:正弦定理

2、ppt(精选)北师大版1正弦定理ppt(精选)北师大版1正弦定理：在一个三角形中，各边和它所对角 的问题1：在ABC中，设 证明：正弦定理ppt(精选)北师大版1正弦定理ppt(精选)北师大版1问题1：在ABC中，设 ACBcba1.正弦定理ppt(精选)北师大版1正弦定理ppt(精选)北师大版1ACBcba1.正弦定理ppt(精选)北师大版1正弦定所以AD=csinB=bsinC, 即同理可得DAcbCB图1过点A作ADBC于D,此时有2.若三角形是锐角三角形, 如图1,正弦定理ppt(精选)北师大版1正弦定理ppt(精选)北师大版1所以AD=csinB=bsinC, 即同理可得DAcbCB

3、图由(1)(2)(3)知，结论成立且仿(2)可得D3.若三角形是钝角三角形,且角C是钝角如图2, 此时也有交BC延长线于D,过点A作ADBC，CAcbB图2正弦定理ppt(精选)北师大版1正弦定理ppt(精选)北师大版1由(1)(2)(3)知，结论成立且仿(2)可得D3.若三角 （2R为ABC外接圆直径）2R求证:4.有没有其他的方法证明以上的等式成立？正弦定理:正弦定理ppt(精选)北师大版1正弦定理ppt(精选)北师大版1（2R为ABC外接圆直径）2R求证:4.有没有其他的证明：OC/cbaCBA作外接圆O,过B作直径BC/,连AC/,A/正弦定理ppt(精选)北师大版1正弦定理ppt(精

4、选)北师大版1证明：OC/cbaCBA作外接圆O,过B作直径BC/,连AC（1）文字叙述正弦定理：在一个三角形中，各边和它所对角 的正弦的比相等.正弦定理:正弦定理ppt(精选)北师大版1正弦定理ppt(精选)北师大版1（1）文字叙述正弦定理：在一个三角形中，各边和它所对角 You try解：正弦定理应用一：已知两角和任意一边，求其余两边和一角正弦定理ppt(精选)北师大版1正弦定理ppt(精选)北师大版1You try解：正弦定理应用一：正弦定理ppt(精例在ABC中，已知a2，b ，A45，求B和c。正弦定理ppt(精选)北师大版1正弦定理ppt(精选)北师大版1例在ABC中，已知a2，b

5、 ，A45例在ABC中，已知a2，b ，A45，求B和c。变式1：在ABC中，已知a4，b ，A45， 求B和c。正弦定理ppt(精选)北师大版1正弦定理ppt(精选)北师大版1例在ABC中，已知a2，b ，A45例在ABC中，已知a2，b ，A45，求B和c。变式2：在ABC中，已知a ，b ，A45， 求B和c。正弦定理ppt(精选)北师大版1正弦定理ppt(精选)北师大版1例在ABC中，已知a2，b ，A45例在ABC中，已知a2，b ，A45，求B和c。变式1：在ABC中，已知a4，b ，A45， 求B和c。变式2：在ABC中，已知a ，b ，A45， 求B和c。正弦定理应用二： 已知

6、两边和其中一边对角，求另一边的对角，进而可求其它的边和角。（要注意可能有两解）正弦定理ppt(精选)北师大版1正弦定理ppt(精选)北师大版1例在ABC中，已知a2，b ，A45点拨：已知两角和任意一边，求其余两边和一角, 此时的解是唯一的.课堂练习:正弦定理ppt(精选)北师大版1正弦定理ppt(精选)北师大版1点拨：已知两角和任意一边，求其余两边和一角,课堂练习:正弦正弦定理ppt(精选)北师大版1正弦定理ppt(精选)北师大版1正弦定理ppt(精选)北师大版1正弦定理ppt(精选正弦定理ppt(精选)北师大版1正弦定理ppt(精选)北师大版1正弦定理ppt(精选)北师大版1正弦定理ppt

7、(精选正弦定理ppt(精选)北师大版1正弦定理ppt(精选)北师大版1正弦定理ppt(精选)北师大版1正弦定理ppt(精选正弦定理ppt(精选)北师大版1正弦定理ppt(精选)北师大版1正弦定理ppt(精选)北师大版1正弦定理ppt(精选正弦定理ppt(精选)北师大版1正弦定理ppt(精选)北师大版1正弦定理ppt(精选)北师大版1正弦定理ppt(精选正弦定理ppt(精选)北师大版1正弦定理ppt(精选)北师大版1正弦定理ppt(精选)北师大版1正弦定理ppt(精选定理应用 课时小结二个 已知两角和一边（只有一解） 已知两边和其中一边的对角 （有一解，两解，无解） 一个 正弦定理CcBbAasinsinsin=正弦定理ppt(