三角函数学案

1、第五章三角函数学案（1）角的推广（一）目标1.掌握用“旋转”定义角的概念，理解并掌握“正角”负角”“象限角”“终边相同的角”的含义；2.掌握所有与角终边相同的角(包括角)的表示方法；3体会运动变化观点，深刻理解推广后的角的概念.复习1初中是如何定义角的？2初中我们所接触的角的范围是新课“（初中所学习的角的意义是否有些狭隘？（在体操比赛中我们经常听到这样的术语：转体720”（即转体2周），转体1080”即转体3周）；如时钟快了5分钟，现要校正，需将分针怎样旋转？如果慢了5分钟，又该如何校正？在奥运会上跳水运动员的跳水难度系数经常有转体多少多少度，这些度数是否超过了我们初中所学角的范围？）1角的新

2、定义：（请试着标出关键词）2推广后的角可以如何进行分类？3什么叫解析法？4象限角是如何定义的？5什么叫做终边相同的角？6试着在0到2000范围内写出与30的终边相同的角.观察有没有什么规律，这样的规律如何表示.结论：所有与终边相同的角连同在内可以构成一个集合：7相等的角终边一定相同，那终边相同的角一定相等吗？例1在0到360范围内，找出与下列各角终边相同的角，并判断它是哪个象限的角.(1)120(2)640(3)95012例2写出与下列各角终边相同的角的集合S，并把S中在360720间的角写出来：（1）60（2）21（3）36314.练习1锐角是第几象限的角？第一象限的角是否都是锐角？小于90

3、的角是锐角吗？090的角是锐角吗？2已知角的顶点与坐标系原点重合，始边落在x轴的正半轴上，作出下列各角，并指出它们是哪个象限的角？(1)420(2)75(3)855(4)510“注意:以后凡是没有给出始边落在x轴的正半轴上”都默认为此条件.作业1下列命题中正确的是()（A）终边在y轴非负半轴上的角是直角（B）第二象限角一定是钝角（C）第四象限角一定是负角（D）若360（Z），则与终边相同2与120角终边相同的角是()（A）600k360，Z（B）120k360，Z（C）120(2k1）180，Z（D）660k360，Z3若角与终边相同，则一定有()（A）180（B）0（C）360，Z（D）36

4、0，Z4与1840终边相同的最小正角为，与1840终边相同的最小正角是.5今天是星期一，100天后的那一天是星期，100天前的那一天是星期.6钟表经过4小时，时针与分针各转了(填度).7在直角坐标系中，作出下列各角(1)360(2)720(3)1080(4)14408已知A锐角，B0到90的角，C第一象限角，D小于90的角求:AB，AC，CD，AD.9将下列各角表示为360（Z，0360）的形式，并判断角在第几象限（1）56024（2）56024（3）290315（4）290315（5）3900（6）390010写出终边落在第一象限角的角集合:写出终边落在第二象限角的角集合:写出终边落在第三象

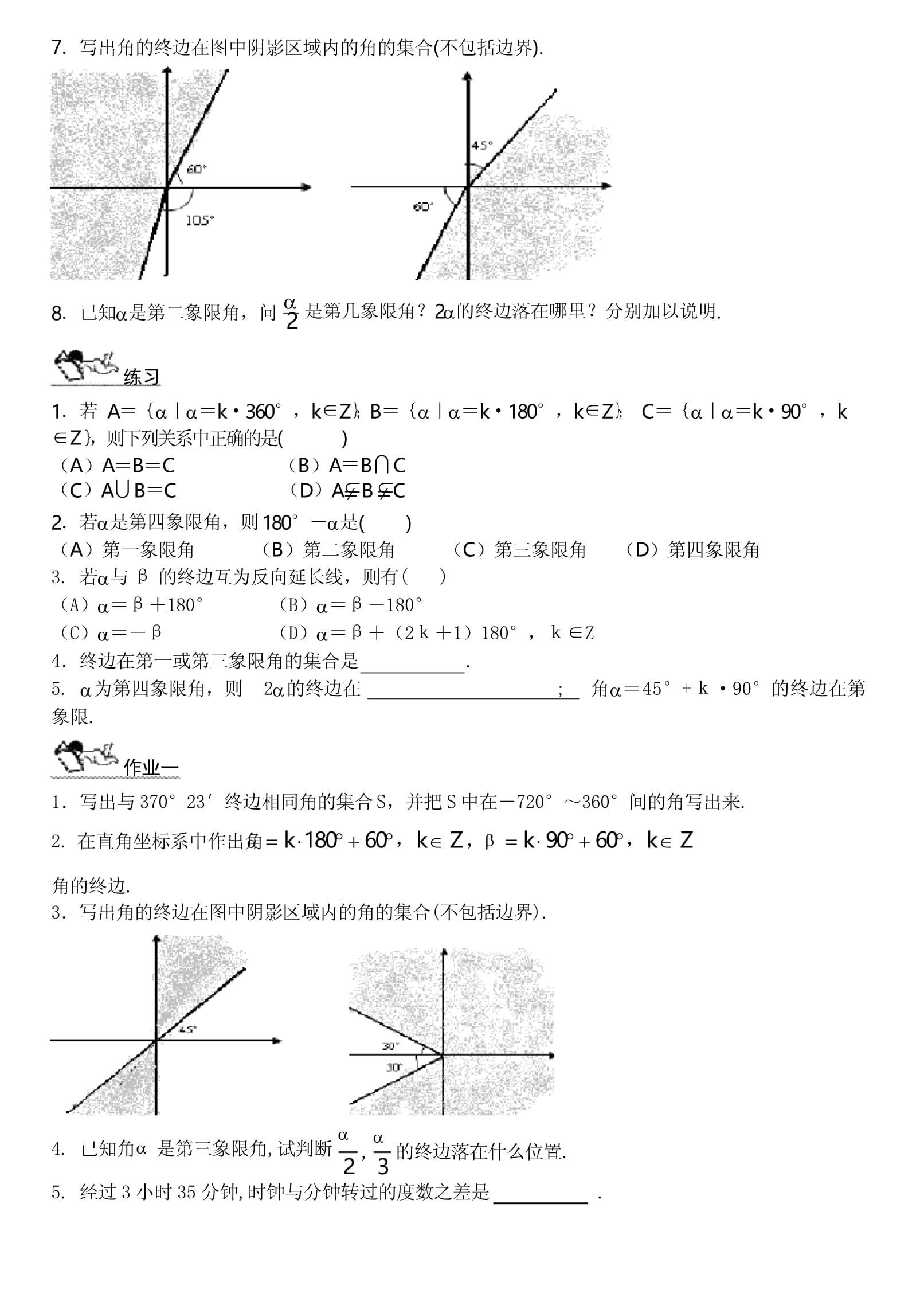
5、限角的角集合:写出终边落在第四象限角的角集合:11试写出终边落在x轴正半轴的所有角的集合:学案（2）角的推广（二）目标1巩固角的形成，正角、负角、零角等概念，熟练掌握掌握所有与角终边相同的角（包括角）、象限角、区间角、终边在坐标轴上的角的表示方法；2掌握所有与角终边相同的角（包括角）、象限角、终边在坐标轴上的角的表示方法；3体会运动变化观点，逐渐学会用动态观点分析解决问题.复习1角的概念的推广.2正角、负角、零角.3象限角、终边相同的角.4写出终边在y轴上的角的集合.5写出所有轴上角的集合.6用区间的形式表示象限角.7写出角的终边在图中阴影区域内的角的集合(不包括边界).2是第几象限角？2的终

6、边落在哪里？分别加以说明.8已知是第二象限角，问（C）ABC（D）ABC练习1若Ak360，kZ；Bk180，kZ；Ck90，kZ，则下列关系中正确的是()（A）ABC（B）ABC2若是第四象限角，则180是()（A）第一象限角（B）第二象限角（C）第三象限角（D）第四象限角3.若与的终边互为反向延长线，则有()（A）180（B）180（C）（D）（21）180，Z4终边在第一或第三象限角的集合是.5.为第四象限角，则2的终边在;角45+90的终边在第象限.作业一1写出与37023终边相同角的集合S，并把S中在720360间的角写出来.2.在直角坐标系中作出角k18060，kZ，k9060，k

7、Z角的终边.3写出角的终边在图中阴影区域内的角的集合(不包括边界).4.已知角是第三象限角,试判断,的终边落在什么位置.235.经过3小时35分钟,时钟与分钟转过的度数之差是.6.集合A|60k360,kZ,B|60k270,kZC|60k180,kZ那么集合A,B,C的关系如何?作业二1在|3601440中与2116终边相同的角有()（A）1个（B）2个（C）3个（D）4个2.在|3601620中与2116终边相同的角有()（A）2个（B）3个（C）4个（D）5个3.角45180，Z的终边落在()（A）第一或第三象限（B）第一或第二象限（C）第二或第四象限（D）第三或第四象限4.第二象限角的

8、集合可表示为.5.角的终边落在一、三象限角平分线上，则角的集合是.6.角是第二象限角，则180是第象限角；是第象限角；180是第_象限角.学案（3）弧度制目标1理解弧度制的定义；2掌握角度与弧度的换算公式并能熟练地进行角度与弧度的换算；3熟记特殊角的弧度数.复习1角的概念的推广.2正角、负角、零角.3象限角、终边相同的角.4写出终边在y轴上的角的集合.5.写出所有轴上角的集合.6.用区间的形式表示象限角.新课1.什么是弧度制？2.弧度与角度如何进行转换？3.试理解下图正角零角负角正实数零负实数4.弧长公式与扇形面积公式：例1把6730化成弧度例2把3rad化成度5注意几点：1度数与弧度数的换算

9、也可借助“计算器”进行；“2今后在具体运算时，弧度”二字和单位符号“rad”可以省略.如：3表示3rad，sin表示rad角的正弦；3一些特殊角的度数与弧度数的对应值应该记住：030456090120135150180270360弧度例3用弧度制表示：1.终边在x轴上的角的集合2.终边在y轴上的角的集合3.终边在坐标轴上的角的集合练习1.下列各对角中终边相同的角是()（A）和222k（Z）（B）22和3371120122（C）和（D）和99392.若3，则角的终边在()（A）第一象限（B）第二象限（C）第三象限（D）第四象限3.若是第四象限角，则一定在()（A）第一象限（B）第二象限（C）第三

10、象限（D）第四象限4.(用弧度制表示)第一象限角的集合为，第一或第三象限角的集合为.5.7弧度的角在第象限，与7弧度角终边相同的最小正角为.6.圆弧长度等于其圆的内接正三角形边长，则其圆心角的弧度数为.3tan7.(选做)求值：sin3tan6cos6tan4cos2.8.已知集合A22，Z，B44，求AB.9.现在时针和分针都指向12点，试用弧度制表示15分钟后，时针和分针的夹角.作业已知是第二象限角，试说明下列各角终边所在位置：(1)(2)(3)223学案（4）三角函数的定义目标1.理解并掌握任意角三角函数的定义；2.理解三角函数是以实数为自变量的函数；3.掌握正弦、余弦、正切函数的定义域

11、.新课在初中，我们对于三角函数的定义是基于直角三角形，而到了高中阶段，我们要在直角坐标系的圆里进行定义.1.设是一个任意角，在的终边上任取（异于原点的）一点P（x,y）则P与原点的距离rx2y2x2y20.2比值yr叫做的正弦记作：sinyrxx比值叫做的余弦记作：cosrry比值叫做的正切记作：tanxyx比值xy叫做的余切记作：cotxy比值rr叫做的正割记作：secxx比值ry叫做的余割记作：cscry2(kZ)时，终边上任意一点P根据相似三角形的知识，对于终边不在坐标轴上确定的角，上述六个比值都不会随P点在的终边上的位置的改变而改变.当角的终边在纵轴上时，即k的横坐标x都为0，所以ta

12、n、sec无意义；当角的终边在横轴上时，即（Z）时，终边上任意一点P的纵坐标都为0，所以cot、csc无意义，除此之外，对于确定的角，上面的六个比值都是惟一确定的实数，这就是说，正弦、余弦、正切、余切、正割、余割都是以角为自变量，以比值为函数值的函数.以上六种函数，统称为三角函数.3.探究:角是“任意角”，当=2k(kZ)时，与的同名三角函数值应该是相等的，即凡是终边相同的角的三角函数值相等.实际上，如果终边在坐标轴上，上述定义同样适用.三角函数是以“比值”为函数值的函数.r0而x,y的正负是随象限的变化而不同，故三角函数的符号应由象限确定.定义域：对于正弦函数sinyy，因为0，所以恒rr有

13、意义，即取任意实数，yr恒有意义，也就是说sin恒有意义，所以正弦函数的定义域是R；类似地可写出余弦函数的定义，因为x0时，域；对于正切函数tanyy无意义，即tanxx无意义，又当且仅当角的终边落在纵轴上时，才有x0，所以当的终边不在纵轴上时，yx恒有意义，即tan恒有意义，所以正切函数的定义域是k2(kZ).从而有：k(kZ)ysinRycotRycosyseck(kZ)2ycscytank(kZ)k(kZ)24.注意:(1)以后我们在平面直角坐标系内研究角的问题，其顶点都在原点，始边都与x轴的非负半轴重合.(2)OP是角的终边，至于是转了几圈，按什么方向旋转的不清楚，也只有这样，才能说明

14、角是任意的.(3)定义中只说怎样的比值叫做的什么函数，并没有说的终边在什么位置(终边在坐标轴上的除外)，即函数的定义与的终边位置无关.(4)比值只与角的大小有关.例1已知角的终边经过点P(2，3)(如图)，求的六个三角函数值.例2填表：030456090120135150180270360弧度sincostancotseccsc例3（1）已知角的终边经过P(4,3),求2sincos的值（2）已知角的终边经过P(4a,3a),(a0)求2sincos的值例4求函数y练习cosxtanxcosxtanx的值域1.若点P(3，)是角终边上一点，且sin23，则的值是.2.角的终边上一个点P的坐标为

15、(5a,12a)(a0)，求sin2cos的值.3.已知sin2cos，求sin4cos5sin2cos及sin22sincos的值.sin04试理解角为第三象限角的充分必要条件是tan05已知tan=3，求下列各式的值.(1)4sincos3sin5cos(2)sin22sincoscos24cos23sin231(3)sin2cos242(5)sincos11(7)sincos(4)sincos(6)sincos(8)sin6cos66若4sin2cos5cos3sin10，则tan的值为.学案（5）同角三角函数的基本关系（一）目标1掌握同角三角函数的基本关系式，理解同角公式都是恒等式的特

16、定意义；2通过运用公式的训练过程，培养解决三角函数求值、化简、恒等式证明的解题技能，提高运用公式的灵活性；3.注意运用数形结合的思想解决有关求值问题；在解决三角函数化简问题过程中，培养思维的灵活性及思维的深化；在恒等式证明的学习过程中，培养分析问题的能力，从而提高逻辑推理能力.复习1.三角函数的概念.2.三角函数值的符号.新课例1已知sin45，并且是第二象限角，求的其他三角函数值.例2已知cos练习817，求sin、tan的值.1已知cos12，求tan的值.2.已知sincos12，求下列各式的值.sin3cos3sin4cos4sin6cos613.已知sincos，且，则cossin的

17、值是多少.842学案（6）同角三角函数的基本关系（二）目标1掌握同角三角函数的基本关系式，理解同角公式都是恒等式的特定意义；2通过运用公式的训练过程，培养解决三角函数求值、化简、恒等式证明的解题技能，提高运用公式的灵活性；3注意运用数形结合的思想解决有关求值问题；在解决三角函数化简问题过程中，培养思维的灵活性及思维的深化；在恒等式证明的学习过程中，培养分析问题的能力，从而提高逻辑推理能力.复习同角三角函数的基本关系公式：sin2cos21sincostancotcossintancot1cscsin1seccos1sin2cos21sec2tan21csc2cot211“同角”的概念与角的表达

18、形式无关，如：2sin2tansin23cos231cos22上述关系（公式）都必须在定义域允许的范围内成立.3一个角的任一三角函数值可求出这个角的其余各三角函数值，且因为利用“平方关系”公式，最终需求平方根，会出现两解，因此应尽可能少用,若使用时,要注意讨论符号.sincos这些关系式还可以如图样加强形象记忆：对角线上两个函数的乘积为1(倒数关系).任一角的函数等于与其相邻的两个函数的积(商数关系).阴影部分，顶角两个函数的平方和等于底角函数的平方(平方关系).新课例1化简：1sin2440.tan1cotseccsc例2已知是第三象限角，化简1sin1sin.1sin1sin例3求证：co

19、s1sin.1sincos求sin的值.，例4已知方程2x2(31)xm0的两根分别是sincos，cos1cot1tanxsincos例5（选讲）消去式子中的：ytancot例6已知sin2sin,tan3tan,求cos2.练习1已知cot=2，求的其余三个三角函数值.2已知：sin15且tan0，试用定义求的其余三个三角函数值.（1）1cos3已知角的终边在直线y=3x上，求sin和cos的值.4化简下列各式，其中(,)21cos1cos1cos（2）sintansin1costansin（3）sin1sin21cos2cos5求证：(2cos2)(12cot2)(2cot2)(2sin

20、2).6已知asecctand,bsecdtanc.求证：a2b2c2d2作业（A）31.已知sincos13，且0，则tan的值为(23（B）3（C）（D）3332.若sin4cos41，则sincos的值为()（A）0（B）1（C）1（D）13.若tancot2，则sincos的值为()（A）0（B）2（C）2（D）24.若tancot=2，则sin4cos4.5.若tan2cot22，则sincos.)6.求证1sin6xcos6x3.1sin4xcos4x27已知tancot2，求sin3cos3的值.学案(7)诱导公式（一）目标1理解并掌握各种三角函数在各象限内的符号；2理解并掌握诱

21、导公式.复习1写出下面函数的定义域ysinycotycosysecytanycsc2上述函数值的正负是什么样的.3终边相同的角的三角函数值有什么样的关系.4终边关于x轴对称的角的三角函数值有什么样的关系.5终边关于y轴对称的角的三角函数值有什么样的关系.6终边关于原点对称的角的三角函数值有什么样的关系.例1确定下列三角函数值的符号.4)(1)cos250（2）sin(例2求下列三角函数的值.（3）tan（672）(4)tan113(1)cos911(2)tan()46例3求值：sin(1320)cos1110+cos(1020)sin750+tan4950练习1确定下列各式的符号(1)sin1

22、00cos240(2)sin5tan52x取什么值时,sinxcosxtanx有意义?5已知是第三象限角且cos0，问是第几象限角？3若三角形的两内角，满足sincos0)的最大值为2,最小值为4，求k,b的值.5求下列函数的定义域：(1)y=3cosx12cos2x(2)y=lg(2sinx1)2cosx1学案（19）三角函数的图象与性质（二）目标1理解正、余弦函数的定义域、值域、最值、周期性、奇偶性的意义；2会求简单函数的定义域、值域、最小正周期和单调区间；3掌握正弦函数yAsin(x)的周期及求法.复习1y=sinx，xR和y=cosx，xR的图象.：2用五点法作正弦函数和余弦函数的简图

23、（描点法）正弦函数y=sinx，x0，2的图象中，五个关键点是：(0,0)(23,1)(,0)(,1)(2,0)2余弦函数y=cosxx0,2的五个点关键是(0,1)(23,0)(,1)(,0)(2,1)23定义域：正弦函数、余弦函数的定义域都是实数集R.分别记作：ysinx，xRycosx，xR4值域正弦函数、余弦函数的值域都是1，1,其中正弦函数y=sinx,xR当且仅当x22k，kZ时，取得最大值1.当且仅当x2k，kZ时，取得最小值1.2而余弦函数ycosx，xR当且仅当x2k，kZ时，取得最大值1.当且仅当x(2k1)，kZ时，取得最小值1.5周期性一般地，对于函数f(x)，如果存在

24、一个非零常数T，使得当x取定义域内的每一个值时，都有f(xT)f(x)，那么函数f(x)就叫做周期函数，非零常数T叫做这个函数的周期.对于一个周期函数f(x)，如果在它所有的周期中存在一个最小的正数，那么这个最小正数就叫做f(x)的最小正周期.1）周期函数x属于定义域M，则必有xTM,且若T0则定义域无上界；T0且A1)的图象可以看作把正数曲线上的所有点的纵坐标伸长(A1)或缩短(0A1)到原来的A倍得到的它的值域A,A最大值是A,最小值是A若A0且1)的图象，可看作把正弦曲线上所有点的横坐标缩短(1)或伸长(01)到原来的1倍（纵坐标不变）若0则可用诱导公式将符号“提出”再作图决定了函数的周

25、期.x3相位变换:函数ysin(x)，R(其中0)的图象，可以看作把正弦曲线上所有点向左(当0时)或向右(当0时)平行移动个单位长度而得到(用平移法注意：“左加”“右减”).新课例1画出函数y3sin(2x3)，xR的简图，观察与y=sinx图象有什么样的关系.例2已知如图是函数y2sin(x)其中的图象，那么()21010（A），（B），111166（C）2，（D）2，66例3已知函数yAsin(x)，在同一周期内，当x函数取得最小值2，则该函数的解析式为()94时函数取得最大值2，当x时9（A）y2sin(3x)（B）y2sin(3x)66xx（C）y2sin()（D）y2sin()363

26、6练习1已知函数yAsin(x)(A0，0，02)图象的一个最高点(2，3)，由这个最高点到相邻最低点的图象与x轴交于点(6，0)，试求函数的解析式.2已知函数yAsin(x)(其中A0，2）在同一周期内，当x时，y有最12小值2，当x712时，y有最大值2，求函数的解析式.3已知函数yAsin(x)在一个周期内，当x7时，取得最大值2，当x时取得最1212小值2，那么()1(A)ysin(x)(B)y2sin(2x)233x(C)y2sin(2x)(D)y2sin()6264如图，已知函数yAsin（x）的部分图象，则函数的表达式为()（A）y2sin（10 x）（B）y2sin（11610 x）116（C）y2sin（2x）（D）y2sin（2x)6615函数y2sin（x）在一个周期内的三个“零点”横坐标是()23511(A),(B)3332410,333112325(C),(D),6663336函数ysin（x2）（0）的周期为2，则7若函数yasinxb（a0)的最小值为13，最大值为，则a、b的值分别为_.228函数y3sin（2x）(0)为偶函数，则.附：作y=sinx（长度为2的某闭区间）沿x轴平移|个单位得y=sin(x+)横坐标伸长或缩短得y=sin(x+)纵坐标伸长或缩短横坐标伸长或缩短