线面平行、面面平行的判定及其性质习题课_第1页
线面平行、面面平行的判定及其性质习题课_第2页
线面平行、面面平行的判定及其性质习题课_第3页
线面平行、面面平行的判定及其性质习题课_第4页
线面平行、面面平行的判定及其性质习题课_第5页
已阅读5页，还剩8页未读， 继续免费阅读

下载本文档

版权说明：本文档由用户提供并上传，收益归属内容提供方，若内容存在侵权，请进行举报或认领

文档简介

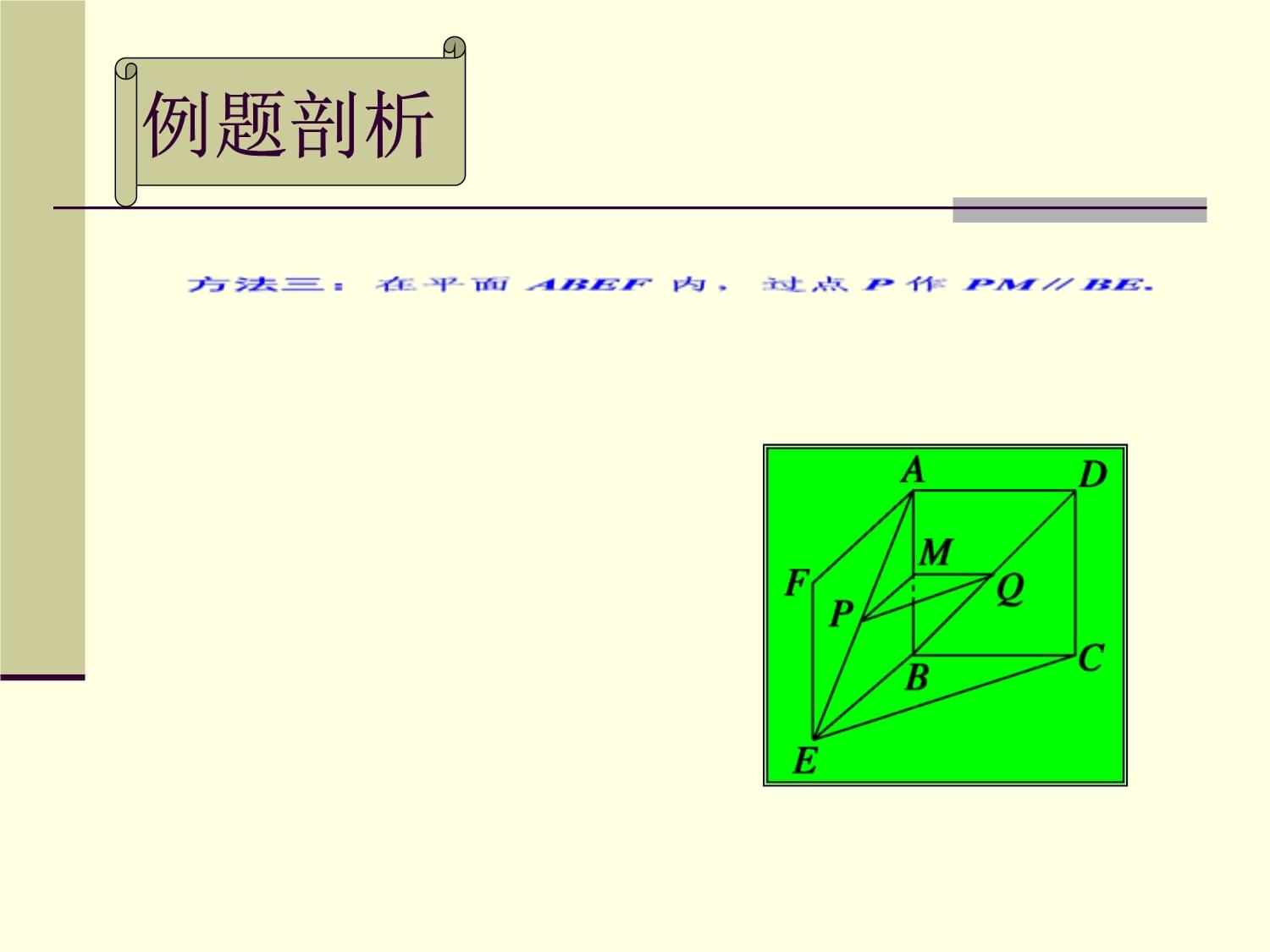
1、2.2 线面平行、面面平行的判定及其性质 习题课线面平行、面面平行的判定线面平行、面面平行的性质【例1】正方形ABCD与正方形ABEF所在平面相交于AB，在AE, BD上各有一点P, Q,且APDQ. 求证：PQ平面BCE.证明:方法一如图, 作PMAB交BE于M, 作QNAB交BC于N,连接MN. 例题剖析例题剖析例题剖析例题剖析【例2】 如图,在底面是平行四边形的四棱锥P-ABCD中,点E在PD上,且PEED=21,在棱PC上是否存在一点F,使BF平面AEC?证明你的结论.解：当F是棱PC的中点时,BF平面AEC.1.下列条件能证明两平面平行的有_。 若一个平面内有两条直线与另一个平面平行

2、；若一个平面内有无数条直线与另一个平面平行；若一个平面内任一条直线都平行于另一个平面；若一个平面内的两条相交直线都平行另一个平面课堂练习2.空间中,下列命题正确的是().A.若a,ba,则bB.若a,b,a,b,则C.若,b,则bD.若,a,则aD课堂练习课堂练习3、如图,在三棱柱ABCA1B1C1中，E，F，G，H分别是AB，AC，A1B1，A1C1的中点，求证:(1)B，C，H，G四点共面； (2)平面EFA1平面BCHG.课堂小结1、证明线面平行的方法：（1）定义法；（2）判定定理；（3）面面平行得线面平行其中判定定理的运用关键是在平面内找一条线与已知直线平行，可构造中位线或平行四边线。

3、2、线面平行怎么用？ 找已知直线所在平面与已知平面的交线。5、区分判定定理与性质定理。3、证明面面平行的方法：（1）定义法；（2）判定定理；（3）垂直于同一直线的两个平面平行；（4）两个平面同时与第三个平面平行，则这两个平面平行。4、面面平行怎么用？（1）线面平行；（2）线线平行；（关键找交线） 如图所示,四边形ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH.求证:APGH.证明:如图所示,连接AC交BD于点O,连接MO.思考题复习回顾 1. 直线与平面的位置关系 直线 a 和平面的位置关系有_、_、_内，其中_ 与_统称直线在平面外. 2. 直线和平面平行的判定 (1)定义：_, 则称直线平行于平面； (2)判定定理：a，b，且ab_; (3)其他判定方法：，a_.平行相交在平面平行相交直线和平面没有公共点复习回顾3.直线和平面平行的性质定理:a,a,=ma_m.4.两个平面的位置关系有_、_5.两个平面平行的判定 (1)定义:_,称这两个平面平行; (2)判定定理:a,b, abA,a,b ; (3)推论：abA，a，b，abA， a，b，aa，bb_.平行相交两个平面没有公共点复习回顾6.

人人文库> 全部分类> 教育资料 > 中学教育

温馨提示

  • 1. 本站所有资源如无特殊说明，都需要本地电脑安装OFFICE2007和PDF阅读器。图纸软件为CAD,CAXA,PROE,UG,SolidWorks等.压缩文件请下载最新的WinRAR软件解压。
  • 2. 本站的文档不包含任何第三方提供的附件图纸等，如果需要附件，请联系上传者。文件的所有权益归上传用户所有。
  • 3. 本站RAR压缩包中若带图纸，网页内容里面会有图纸预览，若没有图纸预览就没有图纸。
  • 4. 未经权益所有人同意不得将文件中的内容挪作商业或盈利用途。
  • 5. 人人文库网仅提供信息存储空间，仅对用户上传内容的表现方式做保护处理，对用户上传分享的文档内容本身不做任何修改或编辑，并不能对任何下载内容负责。
  • 6. 下载文件中如有侵权或不适当内容，请与我们联系，我们立即纠正。
  • 7. 本站不保证下载资源的准确性、安全性和完整性, 同时也不承担用户因使用这些下载资源对自己和他人造成任何形式的伤害或损失。

最新文档

评论

0/150

提交评论